numpy中多项式
作者:互联网
多项式拟合
前言: 任何可微的函数都可以用一个N次多项式来估计, 而比N次幂更高阶的部分为无穷小量.
多项式拟合与线性拟合的区别就是:
线性拟合是使用向量空间中的直线去拟合离散的数据点
多项式拟合是使用连续的曲线去拟合离散的数据点
Key_Function:
np.polyfit函数: 输入x轴数组, 输入y轴数组, 用多项式拟合一系列数据点, 返回一个系数数组
np.polyval函数: 输入多项式系数数组,输入x, 返回一个与x对应的y值
np.roots函数: 输入多项式系数数组, 返回一个表示根的数组
np.poluder函数: 输入多项式系数数组, 返回一个求导后的多项式系数数组
Code:
import numpy as np
import matplotlib.pyplot as plt
bhp = np.loadtxt('BHP.csv', delimiter=',', usecols=(6,), unpack=True)
vale = np.loadtxt('VALE.csv', delimiter=',', usecols=(6,), unpack=True)
print(bhp)
'''
[ 93.72 95.64 94.56 93.3 93.93 92.39 92.11 92.36 91.76 93.91
94.6 93.27 94.43 96.02 95.76 94.47 94.34 92.22 88.31 89.59
89.02 86.95 84.88 87.38 88.56 89.59 88.71 90.02 91.26 90.67]
'''
print(vale)
'''
[ 34.37 35.13 35.14 35.31 35.57 35.03 33.44 33.94 34.21 34.27
34.23 33.76 34.32 34.87 34.5 33.23 33.29 32.88 31.91 32.17
32.44 31.91 31.04 31.51 32.14 32.42 32.25 32.7 32.36 32.34]
'''
t = np.arange(len(bhp))
print(t)
'''
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
25 26 27 28 29]
'''
poly = np.polyfit(t, bhp - vale, 5) # 使用t作为x, bhp-vale作为y,拟合出曲线
print(poly)
'''
[ -9.90778257e-06 1.01779570e-03 -3.46268017e-02 4.62600680e-01
-2.16153196e+00 6.09781428e+01]
'''
poly = np.polyfit(t, bhp - vale, 3) # 改变多项式的阶数
print(poly)
'''
[ 1.11655581e-03 -5.28581762e-02 5.80684638e-01 5.79791202e+01]
'''
# 1.11655581e-03 表示 1.11655581 * 10 ^ -3
# 上述4个值分别表示3次方项系数, 二次方项系数, 一次方项系数, 零次方项系数
# 预测下一个值
print(np.polyval(poly, t[-1] + 1))
# 57.9743076081
# 找到多项式函数的根
print(np.roots(poly))
# [ 35.48624287+30.62717062j 35.48624287-30.62717062j -23.63210575 +0.j ]
# 本例中有三个复根, 关于复根, 见下文详解
# 对多项式函数求导
der = np.polyder(poly)
print(der)
# [ 0.00334967 -0.10571635 0.58068464]
# 这个数组表示倒数的系数, 分别为二次方项, 一次方项, 零次方项
# 求函数的极值点
print(np.roots(der))
# [ 24.47820054 7.08205278]
# 求函数的最大值和最小值
vals = np.polyval(poly, t)
print(np.argmax(vals)) # np.argmax求的是vals的最大值对应的索引, 即x的值
# 7
print(np.argmin(vals)) # np.argmin求的是vals的最小值对应的索引, 即x的值
# 24
plt.plot(t, bhp - vale)
plt.plot(t, vals)
plt.show()

* 使用简单移动平均线或者指数移动平均线, 可以在数据进行拟合前, 对数据进行平滑处理.
关于复数根的解析:
从下文可以看出, 复数是通过扩充定义域的维度, 来求解原本没有解的方程.
如上文得出的三次方多项式, 原本在一维的x下是没有根的, 但是通过给x加旋转, 扩充了x的自由度, 使其有根.
这个三次方多项式, 只表示一个从定义域到值域的映射关系, 至于定义域是什么, 函数并不关心.
什么是虚数
首先,假设有一根数轴,上面有两个反向的点:+1和-1。

这根数轴的正向部分,可以绕原点旋转。显然,逆时针旋转180度,+1就会变成-1。
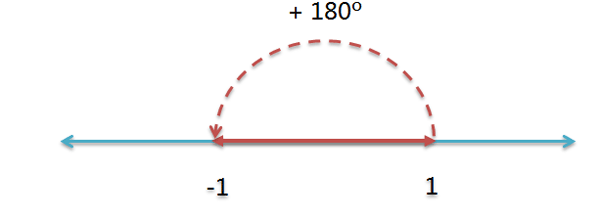
这相当于两次逆时针旋转90度。
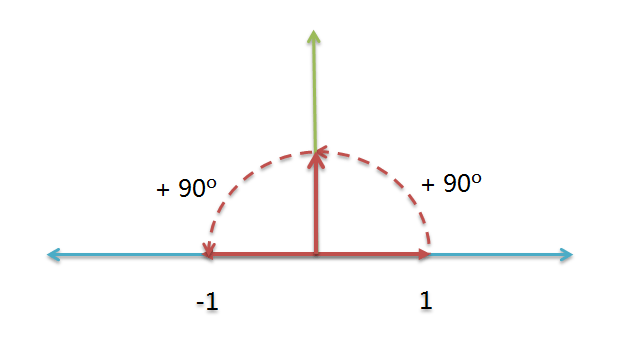
因此,我们可以得到下面的关系式:
(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)
如果把+1消去,这个式子就变为:
(逆时针旋转90度)^2 = (-1)
将"逆时针旋转90度"记为 i :
i^2 = (-1)
这个式子很眼熟,它就是虚数的定义公式。
所以,我们可以知道,虚数 i 就是逆时针旋转90度,i 不是一个数,而是一个旋转量。
复数的定义
既然 i 表示旋转量,我们就可以用 i ,表示任何实数的旋转状态。
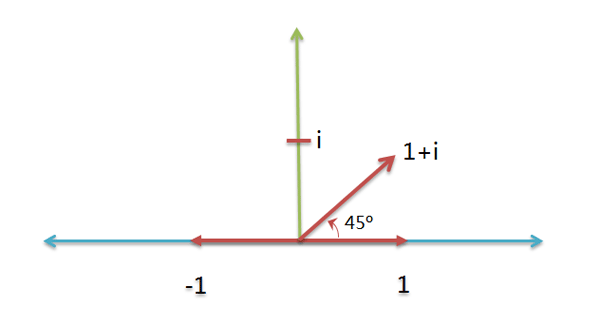
将实数轴看作横轴,虚数轴看作纵轴,就构成了一个二维平面。旋转到某一个角度的任何正实数,必然唯一对应这个平面中的某个点。
只要确定横坐标和纵坐标,比如( 1 , i ),就可以确定某个实数的旋转量(45度)。
数学家用一种特殊的表示方法,表示这个二维坐标:用 + 号把横坐标和纵坐标连接起来。比如,把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。
为什么要把二维坐标表示成这样呢,下一节告诉你原因。
虚数的作用:加法
虚数的引入,大大方便了涉及到旋转的计算。
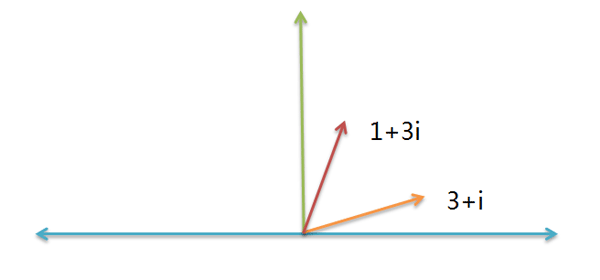
比如,物理学需要计算"力的合成"。假定一个力是 3 + i,另一个力是1 + 3i ,请问它们的合成力是多少?
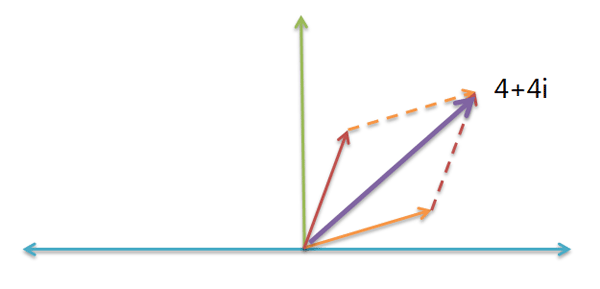
根据"平行四边形法则",你马上得到,合成力就是( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。
这就是虚数加法的物理意义。
虚数的作用:乘法
如果涉及到旋转角度的改变,处理起来更方便。
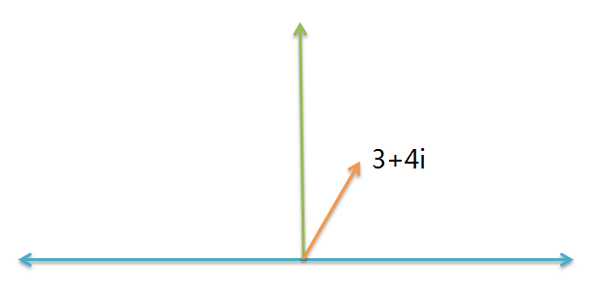
比如,一条船的航向是3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?
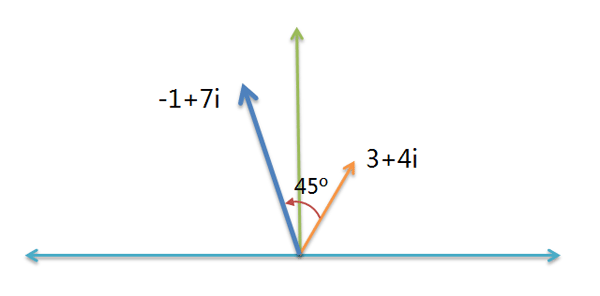
45度的航向就是 1 + i 。计算新航向,只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了(原因在下一节解释):
( 3 + 4i ) * ( 1 + i ) = ( -1 + 7i )
所以,该船的新航向是-1 + 7i。
如果航向逆时针增加90度,就更简单了。因为90度的航向就是 i ,所以新航向等于:
( 3 + 4i ) * i = ( -4 + 3i )
这就是虚数乘法的物理意义:改变旋转角度。
虚数乘法的数学证明
为什么一个复数改变旋转角度,只要做乘法就可以了?
下面就是它的数学证明,实际上很简单。
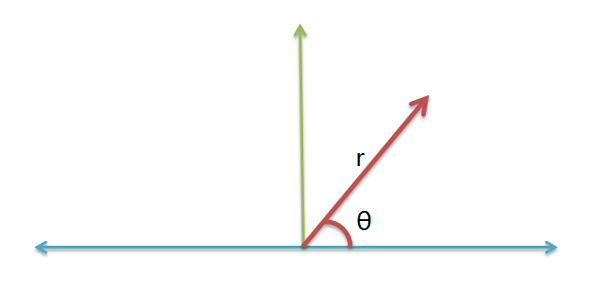
任何复数 a + bi,都可以改写成旋转半径 r 与横轴夹角 θ 的形式。
假定现有两个复数 a + bi 和 c + di,可以将它们改写如下:
a + bi = r1 * ( cosα + isinα )
c + di = r2 * ( cosβ + isinβ )
这两个复数相乘,( a + bi )( c + di ) 就相当于
r1 * r2 * ( cosα + isinα ) * ( cosβ + isinβ )
展开后面的乘式,得到
cosα * cosβ - sinα * sinβ + i( cosα * sinβ + sinα * cosβ )
根据三角函数公式,上面的式子就等于
cos(α+β) + isin(α+β)
所以,
( a + bi )( c + di ) = r1 * r2 * ( cos(α+β) + isin(α+β) )
这就证明了,两个复数相乘,就等于旋转半径相乘、旋转角度相加。
标签:cos,多项式,虚数,旋转,print,np,numpy 来源: https://www.cnblogs.com/draven123/p/11391782.html