【动态规划】洛谷 P1282 多米诺骨牌

时间限制: 1 Sec  内存限制: 128 MB

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

 

 

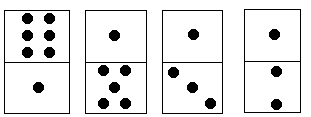
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入格式

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入 #1

4
6 1
1 5
1 3
1 2

输出 #1

1

思路

　　看到题目之后我们分析一下，对于每个骨牌，因为不能改变骨牌上的数字，所以每个骨牌都可以看做是一个零和他们之间的差，当和最小时，是一个很明显的背包问题。

　　以为每个骨牌只有上下两数之差是有意义的，所以我们只用a[i]保存他们两数的差就可以了，不翻即a[i]，翻即-a[i]。

　　我们设f[i][j]为对于前i个骨牌和为j的最小翻动次数，所以很明显f[i][j]=min{f[i-1][j-a[i]],f[i-1][j+a[i]]+1}。

　　但是计算过程中不免会遇到负数，为了防止RE，我们计算一下它的最小值，即-5*1000，所以我们给所有的j都加上一个5000，这样就避免了负数下标的问题。

　　最后扫一遍dp[n][j]就可以找到最佳解啦！

　　话不多说，上代码

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int f[1010][10020];
int a[1010];
int n;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		a[i]=x-y;
	}
	for(int i=0;i<=n;i++)
		for(int j=1;j<=10015;j++)
			f[i][j]=0x3f3f3f3f;
    f[0][0+5010]=0;
    for(int i=1;i<=n;i++)
    	for(int j=10;j<=10010;j++)
    		f[i][j]=min(f[i-1][j-a[i]],f[i-1][j+a[i]]+1);
    int temp=0x3f3f3f3f,ans=0x3f3f3f3f;
    for(int i=10;i<=10010;i++)
    	if(f[n][i]!=0x3f3f3f3f)
    	{
    		if(fabs(i-5010)<=temp)
    		{
    			if(fabs(i-5010)==temp)
    				ans=min(ans,f[n][i]);
    			temp=fabs(i-5010);
    			ans=f[n][i];
    		}
    	}
    printf("%d\n",ans);
    return 0;
}

标签：多米诺骨牌,骨牌,int,P1282,点数,洛谷,include,方块
来源： https://www.cnblogs.com/dawn-whisper/p/11256911.html