首页 > 其他分享> > SVM学习——统计学习理论

SVM学习——统计学习理论

2019-06-25 18:52:53 作者：互联网

关于统计学习的理论博大精深，想要弄明白是需要花费很大功夫的，涉及到方方面面的数学知识(比如泛函分析、高等数学、概率论、统计学…….)，我这里也就是把一些基本概念、理论规整一下。

存在一个未知的系统 $S$ 、给定的输入样本空间 $X$ 和这些输入样本通过 $S$ 处理后的输出 $Y$ 。机器学习的过程可以看做是这样的：利用机器学习的方法，根据 $X$ 和 $Y$ 得到一个学习机(也可以叫模型)，学习机在接受训练、测试样本以外的样本 $X'$ 后得到的输出 $Y'$ 可以被认为是未知系统 $S$ 针对输入 $X'$ 得到的输出的近似，所以这个学习机可以认为是对 $S$ 的内在规律的近似。

实际上，可以将从输入空间产生样本(向量) $x$ 看做从于某个客观存在的、确定的但是未知的概率分布函数 $F(x)$ 中相互独立地抽取出来的；显然由这些 $x$ 通过 $S$ 产生的输出 $y$ 服从 $F(y|x)$ ，而我们的学习器应该是一个函数集合 $f(x,\beta)$ ，这里的 $\beta$ 为参数集合，例如：线性分类器集合为 $f(x,w,b)$ ，通过对 $(w,b)$ 参数的不同取值，我们可以得到一个函数集合；那么寻找这个学习器的过程就变成了从这个函数集合中找出能最佳逼近输入样本的函数。输入 $x$ 和输出 $y$ 服从联合概率分布函数 $F(x,y)=$ $F(x)$ $F(y|x)$ ，也就是说所有训练数据、测试数据的 $(x,y)$ 都是从 $F(x,y)$ 中相互独立地抽取出来的样本。

那么如何衡量逼近是否最佳呢？需要定义一个损失函数： $Loss(f(x,\beta),y)$ (当输入为 $x$ 时，度量学习器的输出 $f(x,\beta)$ 和由系统 $S$ 得出的输出 $y$ 之间的差异)。

还记得连续随机变量函数的数学期望不？设连续随机变量的概率密度为，若其函数 $\eta=f(\zeta)$ ，则随机变量 $\eta$ 的数学期望定义为：

有了上面的概念就可以得到损失的数学期望：

$R(\beta)=$ $E(\beta)=\int{Loss(f(x,\beta),y)}dF(x,y)$

这里 $R(\beta)$ 就是风险泛函，也有人叫期望风险。注意这里的 $x$ 和 $y$ 都是已知的， $F(x,y)$ 是未知的但是确定的，由不同 $\beta$ 确定的 $f(x,\beta)$ 是未知的。

现在就可以将学习过程描述为利用经验数据(就是我们的样本对 $(x,y)$ )最小化风险泛函 $R(\beta)$ 的过程。显然这个 $F(x,y)$ 我们没法知道，那就需要一个替代方案： $R(\beta)=\frac{1}{n}\sum\limits_{i=1}^{n}Loss(f(x_i,\beta),y_i)$ ，于是学习过程就变成了用使经验风险最小的函数逼近使风险泛函最小的函数的过程，这个原则就是传说中的经验风险最小化(ERM)归纳原则。举个体现ERM的例子：回归问题中的最小二乘法(用 $(y-f(x,\beta))^2$ 做 $Loss$ 函数)和概率密度估计中的极大似然法(用 $-lnp(x;,\beta)$ 做 $Loss$ 函数)，哈哈。

把学习问题进行一般化的表示，如下：在空间Z上有一个概率分布 $F(z)$ ，用z代替 $(x,y)$ ， $(z_1,z_2,...z_i)$ 用来代表独立同分布样本，特定的损失函数用 $L(z,\beta)$ 表示，那么风险泛函就表示为：

$R(\beta)=\int{L(z,\beta)}dF(z)$ ，（其中 $\beta$ 为参数集合）

于是经验泛函就表示为：

$R_{emp}(\beta)=\frac{1}{n}\sum\limits_{i=1}^nL(z,\beta)$

最终我们的学习器就是用能最小化 $R_{emp}$ 的函数去逼近能最小化 $R$ 的 $L(z,\beta)$ 。

1、学习过程的一致性

上面的一大堆表示就是为后面的定义和定理做准备的，这些定义和定理是学习理论的基石，我就把我懂得地方说说吧，另外“偷”一些经典的图过来。

定义1：经验风险最小原则下的学习一致性是：下面两个序列依照概率收敛于同一个极限时，则说ERM原则对函数集 $L(z,\beta)$ 和概率分布 $F(z)$ 是一致的。

$R(\beta_i){----- />}\limits_{i->\infty}^{p}inf R(\beta)$ ，（其中 $\beta$ 为参数集合）

$R_{emp}(\beta_i){----- />}\limits_{i->\infty}^{p}inf R(\beta)$ ，（其中 $\beta$ 为参数集合）

我理解这个定义的含义是：满足这个条件就可以保证在经验风险最小的原则下得到的学习方法在训练样本数量趋于无穷的时候可以使期望风险达到最小从而能最好的模拟未知系统S，定义等价于，这个ERM学习方法提供了一个序列 $L(z,\beta_i)$ ， $(i=1,2,...n)$ ，期望风险和经验风险在这个序列上都能收敛到最小可能风险。可以发现这个定义有个问题：如果从函数集去掉某个特定函数后发现它不一致了，就是说函数集的一致性由某个特殊函数决定了，显然这不是我们希望的，这种情况下的一致性叫做平凡一致性，真正对学习有意义的应该是函数集的非平凡一致性。贴个图，

要去除平凡一致性，其实改一改定义就行了。

定义2：对于函数集 $L(z,\beta_i)$ 的任意非空子集 $\Delta$ ：

$\Delta=\int L(z,\beta)dF(z) />c$ ，（其中 $\beta$ 为参数集合， $c \in (-\infty ,+ \infty)$ ）

都有 $R_{emp}(\beta_i){----- />}\limits_{i->\infty}^{p}inf R(\beta)$ ，（其中 $\beta$ 为 $\Delta$ 的参数集合）成立，则说ERM原则对函数集 $L(z,\beta)$ 和概率分布 $F(z)$ 是非平凡一致的。

这个定义等价于从函数集中去掉能最小化风险的函数后上式仍然收敛。

下面这个定理就是传说中的学习理论的关键定理，是大牛Vapnik和Chervonenkis提出的，这个定理要说的是ERM原则一致性的条件取决于函数集中最坏的函数，也就是说基于ERM原则的分析都是“最坏情况分析”，从理论上说，根据ERM原则想要找到一种学习理论能按照“真实情况分析“是八可能的。

定理1：设函数集 $L(z,\beta)$ 满足： $A\leq$ $\int L(z,\beta)dF(z)$ $\leq B$ ，那么ERM原则一致性的充要条件是： $R_{emp}(\beta)$ 是在函数集 $L(z,\beta)$ 上在如下意义下收敛于实际风险 $R(\beta)$ :

$lim_{i- />\infty}P(sup(R(\beta)-R_{emp}(\beta))>\epsilon)=0$ ， $\forall \epsilon />0$ ， $\beta$ 为参数集合 (从这个式子其实可以看出它是单边收敛的，所以也叫单边一致性)

2、学习过程的收敛速度

几个基本概念：用 $N(z_1,z_2,...z_l)$ 表示指示函数集 $L(z,\beta)$ (指示函数是指其函数值只取0和1两个值)中的函数能够把给定样本 $z_1,z_2,...z_l$ 分成多少种不同的分类。

定义3：随机熵， $H(z_1,z_2,...z_l)$ $=ln$ $N(z_1,z_2,...z_l)$ ，它描述的是函数集在给定数据集上的多样性，显然它是个随机数(因为它建立在独立同分布的数据集上)。

定义4：VC熵，随机熵在联合分布函数 $F(z_1,z_2,...z_l)$ 上的数学期望： $H(l)=E$ $ln$ $N(z_1,z_2,...z_l)$ 。

定理1描述的是ERM方法的单边一致性，自然会想到什么时候能满足双边一致性，即： $lim_{i- />\infty}P(sup|R(\beta)-r_{emp}(\beta)|>\epsilon)=0$ ， $\forall \epsilon />0$ ， $\beta$ 为参数集合

定理2：指示函数学习过程双边一致收敛的充分必要条件是：

${lim}\limits_{l- />\infty}\frac{H(\epsilon,l)}{l}$ $=0$

因为双边一致性条件等价于： $lim_{i- />\infty}P(sup(R(\beta)-R_{emp}(\beta))>\epsilon)=0$ 和 $lim_{l- />\infty}P(sup(R_{emp}(\beta)-R(\beta))>\epsilon)=0$ ，所以定理2其实是单边一致性成立的充分条件。

下面在 $N(z_1,z_2,...z_l)$ 的基础上构造两个新概念，然后总结一下传说中的学习理论的三个milestone。

定义5：退火VC熵， $H^'(l)=lnEN(z_1,z_2,...z_l)$

定义6：生长函数， $G(l)$ $=$ $ln({sup}\limits_{z_1,z_2,...z_l}\quad N{(z_1,z_2,...z_l)})$

milestone1：ERM一致性的充分条件，所有的最小化经验风险的学习器都要满足它。

${lim}\limits_{l- />\infty}\frac{H(\epsilon,l)}{l}$ $=0$

milestone2：收敛速度快的充分条件，它保证了收敛有快的收敛的渐进速度。

${lim}\limits_{l- />\infty}\frac{H^'(l)}{l}=0$

milestone3：履行ERM原则的学习器在解决任意问题的时候有一个快的收敛的渐进速度的充要条件。

${lim}\limits_{l- />\infty}\frac{G(l)}{l}=0$

接下来就轮到传奇的VC维出场了，VC维与生长函数有着非常重要的联系，又是一个定理，

定理3：任何生长函数都满足：

$G(l)=l\quad ln2$

或者有一下上界：

$G(l)\leq h(ln{\frac{l}{h}}+1)$ ，其中 $h$ 是一个整数，当 $l=h$ 时满足 $G(h)=hln2$ 和 $G(h)<(h+1)ln2$ 。

直白点说就是：生长函数只能是线性的或者以一个对数函数为上界。

定义4：如果一个样本集含有 $h$ 个样本，它能被某个指示函数集按照所有可能的 $2^h$ 分类方式分为两类，则称该函数集能将样本数为 $h$ 的样本集打散，对于任意指示函数集，它能打散的最大样本集的样本数量，就是它的VC维。由生长函数的定义可以知道，对于一个指示函数集，其生长函数是线性的则其VC维是无穷大的，而如果其生长函数以一个参数为 $h$ 的指数函数为上界，那么它的VC维就是 $h$ 。这就是生长函数和VC维的重要关系。

直观点，举个例子来理解VC维，在二维空间中，如果指示函数集 $L(z,\beta)$ 是线性函数，那么对于空间中三个点A、B、C，将它们分成两类0或者1，可能的组合有 $2^3=8$ 种，分别是： $\left{ \begin{array}{c} A- />0\\ BC->1\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} B- />0\\ AC->1\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} C- />0\\ AB->1\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} A- />1\\ BC->0\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} B- />1\\ AC->0\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} C- />1\\ AB->0\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} ABC- />1\\ \end{array}\right }$ 、 $\left{ \begin{array}{c} ABC- />0\\ \end{array}\right }$ 种，

再增加一个点，那么就应该有 $2^4=16$ 种组合，我就不列出来了，发现没？没有一个线性函数能将B、C分为一类，而A、D分为另一类。(类似于一个单层感知器无法解决异或问题，嘿嘿)

所以在二维空间中线性函数的VC维为3，实际上，推广以后，在n维空间中，线性函数的VC维总是n+1。

遗憾的是目前尚没有一个可以计算任意指示函数集VC维的统一的理论框架，但是这不影响VC维的重要性，它实际上衡量了一个指示函数集的学习性能。

3、控制学习过程的推广能力
控制学习过程的推广能力的理论的目的是构造一种利用小样本训练实例来最小化风险泛函的归纳原则，小样本指的是 $\frac{l}{h}$ 比较小，例如： $20\g$ $\frac{l}{h}$

关于学习器推广能力的界，有以下知识：

假设实函数集合 $L(z,\beta)$ 满足 $A \leq$ $L(z,\beta)$ $\leq B$ (A可以是 $-\infty$ ，B可以是 $+\infty$ )，引入符号 $\epsilon$ ， $\epsilon =4\frac{G^{A,B}(2l)-ln(\eta /4)}{l}$ ，于是对于下面三种情况分别说明：

情况1： $L(z,\beta)$ 是完全有界函数集( $A \leq$ $L(z,\beta)$ $\leq B$ )，下面的不等式以至少 $1-\eta$ 的概率同时对 $L(z,\beta)$ 的所有函数(包括使经验风险最小的函数)成立：

$R(\beta)\leq R_{emp}(\beta)+\frac{(B-A)}{2}\sqrt{\epsilon}$ ，(在 $L(z,\beta)$ 取值只取0、1的二类问题上显然有： $R(\beta)\leq R_{emp}(\beta)+\frac{1}{2}\sqrt{\epsilon}$ )

情况2： $L(z,\beta)$ 是完全有界非负函数集( $0\leq$ $L(z,\beta)$ $\leq B$ )，下面的不等式以至少 $1-\eta$ 的概率同时对 $L(z,\beta)$ 的所有函数(包括使经验风险最小的函数)成立：

$R(\beta)\leq R_{emp}(\beta)+\frac{B\epsilon}{2}(1+\sqrt{1+\frac{4R_{emp}(\beta)}{B\epsilon})$ ，

情况3： $L(z,\beta)$ 是无界非负函数集( $0\leq$ $L(z,\beta)$ )，这种情况下无法得出描述学习器推广能力的不等式，所以需要做如下假设：

$sup(\frac{\int L^p(z,\beta)dF(z)}{\int L(z,\beta)dF(z)})\leq \tau <\infty$ 其中 $p \g 1$

下面的不等式以至少 $1-\eta$ 的概率同时对满足上述假设的所有函数(包括使经验风险最小的函数)成立：

$R(\beta) \leq \frac{R_{emp}(\beta)}{(1-\beta(p)\tau\sqrt\epsilon)_+}$ ，其中 $\beta(p)=\sqrt[p]{\frac{1}{2}(\frac{p-1}{p-2})^{p-1}}$

对于上述情形，如果 $L(z,\beta)$ 包含无穷多个函数且VC维 $h$ 有限，则有：

$\epsilon=4\frac{h(ln\frac{2l}{h}+1)-ln(\frac{\eta}{4})}{l}$

如果 $L(z,\beta)$ 包含N个元素，则有：

$\epsilon=2\frac{lnN-ln\eta}{l}$

上面说了这么多，其实就是想得出在统计学习理论框架下的实际风险到底由什么组成，

$R(\beta)\leq R_{emp}(\beta)+\Phi(\frac{l}{h})$ ，第一部分都知道了，第二部分叫做置信风险

这个式子很令人兴奋，它说明了神马问题呢？

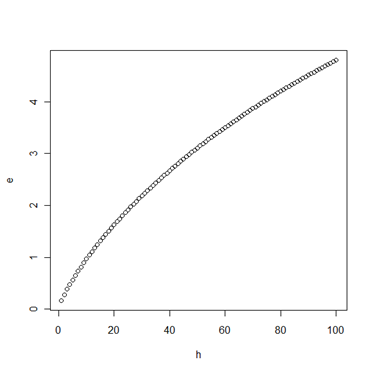
用R画个大概吧：

h=seq(1,100,by=1)

l=seq(1,2000,by=1)

x=l/h

e=4*(log(2*x,base=exp(1))+1)/(x)+(4/l)*(log(0.25/4))

plot(x,e)

当 $\frac{l}{h}$ 比较大的时候 $\epsilon$ 就比较小，从而 $\Phi(\frac{l}{h})$ 就比较小，此时实际风险更加接近经验风险，因此较小的经验风险能保证期望风险也较小。反之，一个小的经验风险不能保证期望风险也较小。

如果样本数固定后再看VC维与置信风险的关系：

l=200

h=seq(1,100,by=1)

x=l/h

e=4*(log(2*x,base=exp(1))+1)/x-4*log(0.25,base=exp(1))/l

plot(h,e)

这说明，当样本数固定的时候，VC维越大，那么置信风险就越大，因而最小化经验风险并不能保证期望风险也较小，所以此时学习结果的推广能力较差，这也就解释了为什么学习器的复杂度越高则越有可能导致overfit。
$R(\beta)\leq R_{emp}(\beta)+\Phi(\frac{l}{h})$ 这个式子里的 $R(\beta)$ 被称作结构风险(SRM)。于是乎，通过上面的分析，就能知道统计学习的目标是什么了吧——学习过程从满足ERM归纳原则变成了满足SRM归纳原则，而SVM就是实现这一原则的算法。

转载于:https://www.cnblogs.com/vivounicorn/archive/2010/12/18/1909709.html

标签：SVM,函数,chart,学习,5C%,0A%,0D%,统计,7D%
来源： https://blog.csdn.net/weixin_34184561/article/details/93642173