树的重量

题目描述

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令N={1..n}，用一个N上的矩阵M来定义树T。其中，矩阵M满足：对于任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。树T满足：
1．叶节点属于集合N；
2．边权均为非负整数；
3．dT(i,j)=M[i,j]，其中dT(i,j)表示树上i到j的最短路径长度。

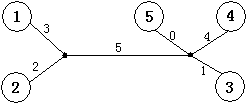
如下图，矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵M。你的任务就是，根据给出的矩阵M，计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树，这棵树的总重量为15。

输入格式

输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行，给出的是矩阵M的一个上三角(不包含对角线)，矩阵中所有元素是不超过100的非负整数。输入数据保证合法。

输入数据以n=0结尾。

输出格式

对于每组输入，输出一行，一个整数，表示树的重量。

分析

一道很好的思维题。题意就是已知一棵树上各点之间的距离，求该树各边长度之和。总体的思路就是一个点一个点地往树上加，在加点的同时统计答案。

以样例的数据为例，首先，我们看只有两个点的情况。

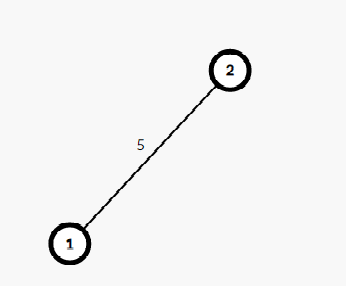
只有两个点的话，显然\(ans=5\)。
接着，我们要继续往树上加点。

第三个点加进来时，因为所有点都必须是叶子节点，所以\(3\)不可能与\(1、2\)直接相连。于是我们只能将\(3\)所连的边加在\(1\)和\(2\)的连边上。此时新加的长度应是\({1 \over 2}(dis[1，3]+dis[2，3]-dis[1，2])=6\)，因此，\(ans+=6\)。
再加上第四个点：

通过加第三个点时我们可以看到，新加的边的长度可以通过另外两个点算出来，新加边的位置也由我们使用的两点来决定。那么在加第四个点的时候，我们应该用哪两个点来算呢？尝试也用\(1\)和\(2\)来算，发现\({1 \over 2}(dis[1，4]+dis[2，4]-dis[1，2])=9\ne4\) ，这是因为\(4\)所连接的节点并不在\(1、2\)连边上，导致我们多算了长度为\(5\)的这条边。而选\(1、3\)两个点或\(2、3\)两个点，我们都可以得到答案\(4\)。因此\(ans+=4\)。

通过观察我们发现，若（使用\(i、j\)两个点计算得来的长度\(）>（使用k、l\)两个点得到的长度），就说明对于\(i、j\) ，我们多计算了某条边，自然得到的结果不是实际结果。因此，当我们每次加点的时候，枚举\(i、j\)，表示该点是在\(i、j\)的连边上所得到的答案，再取个最小值即可。

代码

代码十分简单，但分析过程很有价值。

#include<bits/stdc++.h>
#define MAXN 40
using namespace std;
int n,x,ans=0;
int mat[MAXN][MAXN]={0};
int main()
{
	while(1)
	{
		scanf("%d",&n);
		if(!n)break;
		ans=0;
		for(int i=1;i<n;i++)
			for(int j=i+1;j<=n;j++)
				scanf("%d",&mat[i][j]);
		for(int i=2;i<=n;i++)
		{
			x=mat[1][i];
			for(int j=1;j<i;j++)
				for(int k=j+1;k<i;k++)
					x=min(x,(mat[j][i]+mat[k][i]-mat[j][k])/2);
			ans+=x;
		}
		printf("%d\n",ans);
	}
	return 0;
}

又水了一篇博客~ ~ ~
(逃

标签：int,重量,矩阵,ans,长度,dis
来源： https://www.cnblogs.com/huled/p/16692591.html