特征选择

模型默认的Feature Importance存在什么问题？

Feature Importance的本质是训练好的模型对变量的依赖程度，它不代表变量在unseen data（比如测试集）上的泛化能力。特别当训练集和测试集的分布发生偏移时，模型默认的Feature Importance的偏差会更严重。

举一个极端的例子，如果我们随机生成一些X和二分类标签y，并用XGB不断迭代。随着迭代次数的增加，训练集的AUC将接近1，但是验证集上的AUC仍然会在0.5附近徘徊。这时模型默认的Feature Importance仍然会有一些变量的重要性特别高。这些变量帮助模型过拟合，从而在训练集上实现了接近1的AUC。但实际上这些变量还是无意义的。

2 什么是Permutation Importance？

Permutation Importance是一种变量筛选的方法。它有效地解决了上述提到的两个问题。

Permutation Importance将变量随机打乱来破坏变量和y原有的关系。如果打乱一个变量显著增加了模型在验证集上的loss，说明该变量很重要。如果打乱一个变量对模型在验证集上的loss没有影响，甚至还降低了loss，那么说明该变量对模型不重要，甚至是有害的。

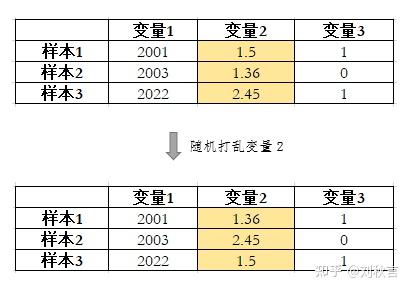打乱变量示例

变量重要性的具体计算步骤如下：

• 1. 将数据分为train和validation两个数据集
• 2. 在train上训练模型，在validation上做预测，并评价模型（如计算AUC）
• 3. 循环计算每个变量的重要性：
• （3.1） 在validation上对单个变量随机打乱；
• （3.2）使用第2步训练好的模型，重新在validation做预测，并评价模型；
• （3.3）计算第2步和第3.2步validation上模型评价的差异，得到该变量的重要性指标

Python代码步骤（model表示已经训练好的模型）：

def permutation_importances(model, X, y, metric):
    baseline = metric(model, X, y)
    imp = []
    for col in X.columns:
        save = X[col].copy()
        X[col] = np.random.permutation(X[col])
        m = metric(model, X, y)
        X[col] = save
        imp.append(baseline - m)
    return np.array(imp)

3 Permutation Importance的优劣势是什么？

3.1 优势

• 可以在任何模型上使用。不只是在基于决策树的模型，在线性回归，神经网络，任何模型上都可以使用。
• 不存在对连续型变量或高基数类别型变量的偏好。
• 体现了变量的泛化能力，当数据发生偏移时会特别有价值。
• 相较于循环的增加或剔除变量，不需要对模型重新训练，极大地降低了成本。但是循环地对模型做预测仍然会花费不少时间。

3.2 劣势

• 对变量的打乱存在随机性。这就要求随机打乱需要重复多次，以保证统计的显著性。
• 对相关性高的变量会低估重要性，模型默认的Feature Importance同样存在该问题。

标签：变量,特征选择,模型,Feature,col,Importance,打乱
来源： https://www.cnblogs.com/qiaoqifa/p/16689978.html