首页 > 其他分享> > cold diffusion的个人理解

cold diffusion的个人理解

2022-09-13 13:32:35 作者：互联网

背景和介绍

最近阅读了 Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise，做了个简短的汇报，写一篇博客记录一下。

目前的diffusion model都是基于高斯噪声在进行扩散，其可被理解为使用Langeviin dynamics在数据范围游走。
对于反向生成而言，就是从一个噪声，一点点的降噪到几乎没有噪声的状态。

本文探索了一种新的生成方式，其并不依赖于高斯噪声

宏观视角看cold diffusion

先考虑DDPM：

其模型关键有这么几步：

给图像加随机高斯噪声，得到不同t时刻对应的\(x_t\)，可推得\(x_T\)符合标准高斯分布
从标准高斯分布中取一个样本，反向执行加噪操作，最后生成\(x_{0}\)

其实也可以理解成这个过程：

给图像进行退化操作，得到不同t时刻对应的\(x_t\)，可推得\(x_T\)符合某个分布
从\(x_T\) 符合的分布中取一个样本，反向前向的退化过程从而生成\(x_{0}\)

换言之，如果我想要对图像进行其他的退化操作，就一定要：

知道\(x_T\) 符合的分布
有一种很好的反向sampling的计算方式。

在DDPM中，图像的加噪围绕噪声，降噪围绕噪声，网络的训练目标是去近似噪声。噪声贯穿始终。

而此时因为模型需要可以适用于任何的变换，相当于需要站在一个更高的层次看diffusion model，自然不能将关注点放在具体的变换方式上，因此需要一个采取任何变换时都公有的存在来表示模型的退化变化、训练目标。

很容易想到，既然不能在“退化方式”的基础上建模，那就关注数据分布本身的情况\(x_0,x_1,x_2...x_T\)。在这个基础上，我们只要知道，正向退化时会把数据弄成什么样，反向恢复时，数据要如何一步步拟合到数据集的情况。同时，神经网络模型只能用于预测\(x_0\)。

因此，引入如下记号：
图像退化算子(image degradation operator)，
图像恢复算子(image restoration operator)，
两者定义如下：其中将 t 理解为图像的受损程度(severity)

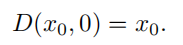
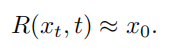
让模型去预测\(x_0\) ，用 \(\bar{x_0}与x_0\)的范数来衡量模型的预测效果。

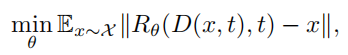
加一些些细节分析

关于图像的退化操作：

对于DDPM，退化过程可以时每次随机加噪，因为数学推导告诉我，最后的分布一定是符合标准高斯分布的。
所以我们有：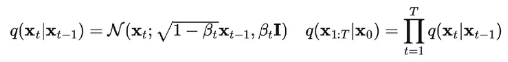
对于其他的退化方式，由于生成样本时需要从\(x_T\) 符合的分布中取样本，也就是说，我们需要给图像退化过程增加限定，使得最后\(x_T\) 分布是已知的。

采用其它的图像退化方式，最终的分布往往是足够简单但是不可事先确认（例如：采用模糊的方式退化图像时，知道最后的分布是一张纯色图）

关于图像恢复操作：

作者提出了两种算法：

Algorithm 1：
存在较大的问题，如果恢复算子R可以完美恢复至\(x_0\)，那么显然没有问题。
但其恢复一般不是完美符合的，每一次使用R都会增大误差，那么一来一回偏差就会变大。
同时作者指出：algorithm1可以很好地适用于基于噪声的扩散，可能是因为恢复算子R已经被训练来纠正其输入中的误差。但其应对cold diffusion这种变化较为的情况时，效果较差。

Algorithm 2：
其相比于algorithm1，其具有更好的数学特性，尤其是下面一类的线性变换。

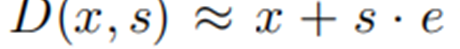
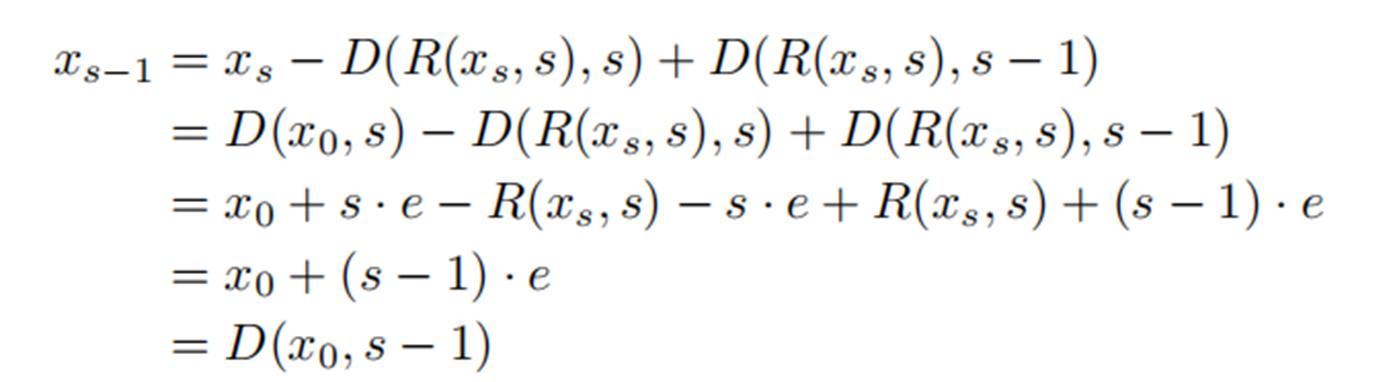
显然在这种变换时，即便R没有很好的拟合，也能有很好的效果

看一个例子

将另一个数据集的数据分布作为\(x_T\) 的分布进行处理。此例中用的是celebA和APHQ。\(人脸\to 动物脸 \to 人脸\)

图像退化过程：

这个图像退化的方式其实就是DDPM中加噪的公式，只是\(z\) 代表的含义不一样。

加载数据：

# 此处的dl借助了cycle形成了无限循环的迭代器。
# dl1为celebA数据集， dl2为APHQ数据集（动物脸）
self.dl1 = cycle(data.DataLoader(self.ds1, batch_size = train_batch_size, shuffle=shuffle, pin_memory=True, num_workers=16, drop_last=True))
self.dl2 = cycle(data.DataLoader(self.ds2, batch_size = train_batch_size, shuffle=shuffle, pin_memory=True, num_workers=16, drop_last=True))

训练过程：

并不是一个epoch中训练整个数据集，而是规定了一个epoch中训练的次数，循环取数据进行训练

# 与常规的训练不同，因为训练方式为限定一个epoch中的训练次数，一次训练就会取一个batch_size的数据进行训练
def train(self):
    
    backwards = partial(loss_backwards, self.fp16)

    acc_loss = 0
    while self.step < self.train_num_steps:		# 相当于epoch
        for i in range(self.gradient_accumulate_every):	# 规定了一个epoch中的训练次数
            data_1 = next(self.dl1).cuda()		# 取数据是采用循环取数据的方式实现的
            data_2 = next(self.dl2).cuda()
            loss = torch.mean(self.model(data_1, data_2))
		

# loss的计算            
def p_losses(self, x_start, x_end, t):
    b, c, h, w = x_start.shape
    if self.train_routine == 'Final':	# 不用管
        x_mix = self.q_sample(x_start=x_start, x_end=x_end, t=t)	# 图像退化后的结果
        x_recon = self.denoise_fn(x_mix, t)		# 使用R恢复后的图像结果
        # 两种不同的loss计算方法
        if self.loss_type == 'l1':		
            loss = (x_start - x_recon).abs().mean()
        elif self.loss_type == 'l2':
            loss = F.mse_loss(x_start, x_recon)
        else:
            raise NotImplementedError()
	return loss


# 具体的加噪过程 q_sample
def q_sample(self, x_start, x_end, t):  # x_start训练图像  x_end为加噪的图片
    # simply use the alphas to interpolate
    return (
        extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
        extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * x_end
    )

sampling：

# sample的全过程
def test_from_data(self, extra_path, s_times=None):
    batches = self.batch_size
    og_img = next(self.dl2).cuda()	# 从APFQ数据集中随机取出一张图片
    X_0s, X_ts = self.ema_model.module.all_sample(batch_size=batches, img=og_img, times=s_times)
    

# 此为实际执行降噪过程的函数
@torch.no_grad()
def all_sample(self, batch_size=16, img=None, t=None, times=None, eval=True):
    if eval:
        self.denoise_fn.eval()
	if t == None:
        t = self.num_timesteps
        
    X1_0s, X2_0s, X_ts = [], [], []
    while (t):
        step = torch.full((batch_size,), t - 1, dtype=torch.long).cuda()
        x1_bar = self.denoise_fn(img, step)     # 应用训练的网络，直接得到的初始图像
        x2_bar = self.get_x2_bar_from_xt(x1_bar, img, step) # 图片退化时的图，即z

        X1_0s.append(x1_bar.detach().cpu())   
        X2_0s.append(x2_bar.detach().cpu())
        X_ts.append(img.detach().cpu())

        xt_bar = x1_bar
        if t != 0:
            xt_bar = self.q_sample(x_start=xt_bar, x_end=x2_bar, t=step)	# 对应公式中的D(x0, t)

        xt_sub1_bar = x1_bar
        if t - 1 != 0:
            step2 = torch.full((batch_size,), t - 2, dtype=torch.long).cuda()
            xt_sub1_bar = self.q_sample(x_start=xt_sub1_bar, x_end=x2_bar, t=step2) # 对应公式中的D(x0, t-1)

        x = img - xt_bar + xt_sub1_bar	# 最终得到的，对应公式中的x_(t-1)
        img = x
        t = t - 1
    return X1_0s, X_ts

有一个小问题：

此处\(x_T\)的分布是由另一个数据集的情况给定的，如果采用blur、inpaint之类的方式退化图像，怎么知道\(x_T\) 的分布？
- 在sampling时，从数据集中去一个\(x_0\)，计算出\(x_T\)，将其作为反向生成图像的起点。
  作者在文中提到了GMM，我没太看明白
但这样做有一个问题：反向生成出的图像有很高的质量，但是多样性很低，如何处理？
- 给\(x_T\) 加一个值很小的高斯噪声

个人的一些理解

与加噪的那些模型相比

加噪的模型能够保证最终的模型是一个高斯分布，因此加噪时可以随机，反正最后的结果是高斯分布。给定一个\(x_0\)，跑100次最后可以得到100个不同的\(x_T\)。
cold diffusion：需要保证图像退化的最终分布的可预测性。如果图像退化过程是随机的话，那么无法保证最终的结果，因此加噪过程是一个可变性很小的过程。实际上，对于很多退化方式，\(x_0\)对应的\(x_T\)是固定的。

本模型与DDPM最大的不同，就是根本不关系加噪的方式，将目光放到了不同t时的数据本身上。

这个模型不关心图片退化的方式。对于代码，如果需要修改图片退化方式，只需要改q_sample()（图片退化函数）这一个函数就好，其它的几乎不用改。

这篇论文的精华就是它提出的algorithm2和恢复算子R的概念，两者合在一起组成的模型可以用于任意噪声。其对于相对线性的的变化，在反向拟合过程有着很好的效果。

标签：diffusion,loss,bar,self,start,理解,退化,图像,cold
来源： https://www.cnblogs.com/tantor/p/16688813.html