二进制的原码、反码、补码
作者：互联网
二进制的原码、反码、补码
狂风吹我心
马之千里者
一、十进制与二进制的相互转换
1. 十进制转换为二进制，分为整数部分和小数部分。
整数部分采用除2倒取余法，具体做法：用2去除十进制整数，可以得到一个商和余数；在用2去除商，又会得到一个商和余数，如此进行，知道商为0时为止，然后把先的到的余数作为二进制的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
小数部分采用乘2取整法，具体做法：用2乘十进制小数，可以得到积，将积中的整数部分取出，在用2乘余下的小数部分，又得到一个积，在将积中的整数部分取出，如此进行，直到积中的小数部分为0，此时0或1为二进制的最后一位，或者达到所要求的精度为止，然后把取出的整数部分按顺序排列起来，先取得整数作为二进制小数的最高位有效位，后取的整数作为低位有效位。
2. 二进制转换为十进制，方法：按权相加法，即将二进制每位上的数乘以权，然后相加之和即是十进制数。
二、预备知识
由于计算机的硬件决定，任何存储于计算机中的数据，其本质都是以二进制码存储。
根据冯·诺依曼提出的经典计算机体系结构框架，一台计算机由运算器、控制器、存储器、输入和输出设备组成。其中运算器只有加法运算器，没有减法运算器（据说一开始是有的，后来由于减法运算器硬件开销太大，被废了）。
所以计算机中没办法直接做减法的，它的减法是通过加法实现的。现实世界中所有的减法也可以当成加法的，减去一个数可以看作加上这个数的相反数，但前提是要先有负数的概念，这就是为什么不得不引入一个符号位。符号位在内存中存放的最左边一位，如果该位位0，则说明该数为正；若为1，则说明该数为负。
而且从硬件的角度上看，只有正数加负数才算减法，正数与正数相加，负数与负数相加，其实都可以通过加法器直接相加。
原码、反码、补码的产生过程就是为了解决计算机做减法和引入符号位的问题。
三、原码
原码：是最简单的机器数表示法，用最高位表示符号位，其他位存放该数的二进制的绝对值。
以带符号位的四位二进制数为例：1010，最高位为1表示这是一个负数，其它三位010，即0*2^2+1*2^1+0*2^0=2，所以1010表示十进制数-2。
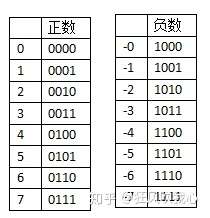部分正负数的二进制原码表示
原码的表示法很简单，虽然出现了+0和-0，但是直观易懂。于是开始运算——
0001+0010=0011，1+2=3；
0000+1000=1000，+0+(-0)=-0；
0001+1001=1010，1+(-1)=-2。
于是可以看到其实正数之间的加法通常是不会出错的，因为它就是一个很简单的二进制加法，而正数与负数相加，或负数与负数相加，就要引起莫名其妙的结果，这都是符号位引起的。0分为+0和-0也是因它而起。
原码的特点：
1. 原码表示直观、易懂，与真值转换容易。
2. 原码中0有两种不同的表示形式，给使用带来了不便。
通常0的原码用+0表示，若在计算过程中出现了-0，则需要用硬件将-0变成+0。
3. 原码表示加减运算复杂。
利用原码进行两数相加运算时，首先要判别两数符号，若同号则做加法，若异号则做减法。在利用原码进行两数相减运算时，不仅要判别两数符号，使得同号相减，异号相加；还要判别两数绝对值的大小，用绝对值大的数减去绝对值小的数，取绝对值大的数的符号为结果的符号。可见，原码表示不便于实现加减运算。
四、反码
原码最大的问题就在于一个数加上它的相反数不等于0，于是反码的设计思想就是冲着解决这一点，既然一个负数是一个正数的相反数，那干脆用一个正数按位取反来表示负数。
反码：正数的反码还是等于原码；负数的反码就是它的原码除符号位外，按位取反。
以带符号位的四位二进制数为例：3是正数，反码与原码相同，则可以表示为0011；-3的原码是1011，符号位保持不变，低三位按位取反，所以-3的反码为1100。
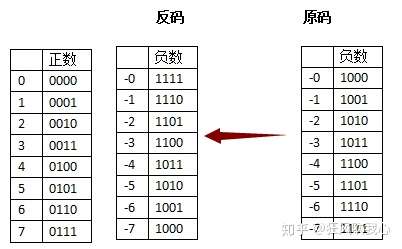部分正负数的二进制反码表示
再试着用反码的方式解决一下原码的问题——
0001+1110=1111，1+(-1)=-0；
1110+1100=1010，(-1)+(-3)=-5。
互为相反数相加等于0，虽然的到的结果是1111也就是-0。但是两个负数相加的出错了。
反码的特点：
- 在反码表示中，用符号位表示数值的正负，形式与原码表示相同，即0为正；1为负。
- 在反码表示中，数值0有两种表示方法。
- 反码的表示范围与原码的表示范围相同。
反码表示在计算机中往往作为数码变换的中间环节。
五、补码
补码：正数的补码等于它的原码；负数的补码等于反码+1（这只是一种算补码的方式，多数书对于补码就是这句话）。
其实负数的补码等于反码+1只是补码的求法，而不是补码的定义，很多人以为求补码就要先求反码，其实并不是，那些计算机学家并不会心血来潮的把反码+1就定义为补码，只不过补码正好就等于反码+1而已。
如果有兴趣了解补码的严格说法，建议可以看一下《计算机组成原理》，它会用“模”和“同余”的概念，严谨地解释补码。
六、补码的思想
补码的思想，第一次见可能会觉得很绕，但是如果肯停下来仔细想想，绝对会觉得非常美妙。
补码的思想其实就是来自于生活，只是我们没注意到而已，如时钟、经纬度、《易经》里的八卦等。补码的思想其实就类似于生活中的时钟。
如果说现在时针现在停在10点钟，那么什么时候会停在八点钟呢？
简单，过去隔两个小时的时候是八点钟，未来过十个小时的时候也是八点钟。
也就是说时间倒拨2小时，或正拨10小时都是八点钟。
也就是10-2=8，而且10+10=8。
这个时候满12，说明时针在走第二圈，又走了8小时，所以时针正好又停在八点钟。
所以12在时钟运算中，称之为模，超过了12就会重新从1开始算了。
也就是说，10-2和10+10从另一个角度来看是等效的，它都使时针指向了八点钟。
既然是等效的，那么在时钟运算中，减去一个数，其实就相当于加上另外一个数（这个数与减数相加正好等于12，也称为同余数），这就是补码所谓运算思想的生活例子。
在这里，再次强调原码、反码、补码的引入是为了解决做减法的问题。在原码、反码表示法中，我们把减法化为加法的思维是减去一个数等于加上这个数的相反数，结果发现引入符号位，却因为符号位造成了各种意想不到的问题。
但是从上面的例子中，可以看到其实减去一个数，对于数值有限制、有溢出的运算（模运算）来说，其实也相当于加上这个数的同余数。
也就是说，不引入负数的概念，就可以把减法当成加法来算。
七、补码的实例
接下来就做一做四位二进制数的减法（先不引入符号位）。
0110-0010，6-2=4，但是由于计算机中没有减法器，没法算。
这时候，想想时钟运算中，减去一个数，是可以等同于加上另外一个正数（同余数），这个数与减数相加正好等于模。
也就是四位二进制数最大容量是多少？其实就是2^4=16（10000）。
那么-2的同余数，就等于10000-0010=1110，16-2=14。
既然如此，0110-0010=0110+1110=10100，6-2=6+14=20。
按照这种算法得出的结果是10100，但是对于四位二进制数最大只能存放4位，如果低四位正好是0100，正好是想要的结果，至于最高位的1，计算机会把它放入psw寄存器进位位中，8位机会放在cy中，x86会放在cf中，这里不做讨论。
这个时候，再想想在四位二进制数中，减去2就相当于加上它的同余数（至于它们为什么同余，还是建议看《计算机组成原理》）。
但是减去2，从另一个角度来说，也是加上-2，即加上-2和加上14得到的二进制结果除了进位位，结果是一样的。如果我们把1110的最高位看作符号位后就是-2的补码，这可能也是为什么负数的符号位是1，而不是0。
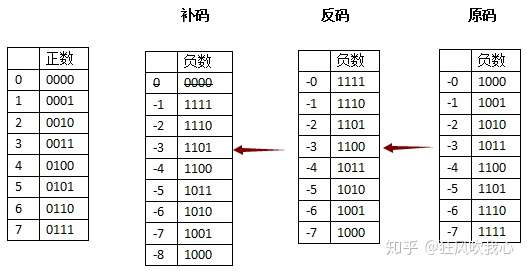部分正负数的二进制补码表示
到这里，原码、反码的问题，补码基本解决了。
在补码中也不存在-0了，因为1000表示-8。
补码的特点：
1. 在补码表示中，用符号位表示数值的正负，形式与原码的表示相同，即0为正，1为负。但补码的符号可以看做是数值的一部分参加运算。
正数的补码表示就是其本身，负数的补码表示的实质是把负数映像到正值区域，因此加上一个负数或减去一个正数可以用加上另一个数（负数或减数对应的补码）来代替。
从补码表示的符号看，补码中符号位的值代表了数的正确符号，0表示正数，1表示负数；而从映像值来看，符号位的值是映像值的一个数位，因此在补码运算中，符号位可以与数值位一起参加运算。
2. 在补码表示中，数值0只有一种表示方法。
3. 负数补码的表示范围比负数原码的表示范围略宽。纯小数的补码可以表示到-1，纯整数的补码可以表示到-2^n。
由于补码表示中的符号位可以与数值位一起参加运算，并且可以将减法转换为加法进行运算，简化了运算过程，因此计算机中均采用补码进行加减运算。
八、为什么负数的补码的求法是反码+1
因为负数的反码加上这个负数的绝对值正好等于1111，在加1，就是10000，也就是四位二进数的模，而负数的补码是它的绝对值的同余数，可以通过模减去负数的绝对值得到它的补码，所以负数的补码就是它的反码+1。
标签：反码,符号,二进制,补码,负数,原码 来源： https://www.cnblogs.com/fengjiale/p/16680165.html