首页 > 其他分享> > 题解洛谷 P2700 【逐个击破】

题解洛谷 P2700 【逐个击破】

2022-09-10 03:01:08 作者：互联网

\(P2700\) 逐个击破

前置知识

克鲁斯卡尔最小生成树算法并查集贪心思想

题目描述

给出一颗带权的树，删除任意条边，求出使得给定的点不连通的最小权值。

解题思路

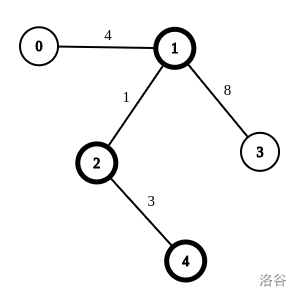
sample
样例说明：删除权值为\(1\)和\(3\)的边，使得\(1.2.4\)三点不连通，答案为\(1 + 3 = 4\)。

使删除的边总权值最小可以转化为使添加的边总权值最大。
借鉴克鲁斯卡尔算法的基本思想：贪心地选取当前未被选过的权值最大的边，将其建入图内，直至所有的非指定点都被并入图内。
统计出加入的边的权值，答案即为总边权 - 统计出的边权。

\[Ans = tot - cnt \]

注意事项

1.按边权从大到小排序。
2.数据范围大，用 \(long long\) 存变量。

#include <bits/stdc++.h>
#define re register
#define il inline
#define ll long long
#define MAXN 100005
#define MAXM 100005
#define rep(i,a,b)  for(re int i = a;i <= b;++ i)
#define Rep(i,a,b)  for(re int i = a;i < b;++ i)
#define drep(i,a,b) for(re int i = a;i >= b;-- i)
#define fin(a)  freopen(#a".in","r",stdin)
#define fout(a) freopen(#a".out","w",stdout)

using namespace std;

struct edge{
    int u,v,w;
}e[MAXM];
int n,k;
int fa[MAXN];
bool p[MAXN];
ll ans = 0;

il bool cmp(edge a,edge b){
    return a.w > b.w;
}

il int find(int x){
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

il void kruskal(){
    Rep(i,1,n){
        int u = e[i].u,v = e[i].v,w = e[i].w;
        int fu = find(u),fv = find(v);
        if(p[fu] && p[fv])
            continue;
        
        fa[fu] = fv;
        ans -= w;

        if(p[fu])
            p[fv] = 1;
        else
            if(p[fv])
                p[fu] = 1;
    }
}



int main(){
    #ifndef ONLINE_JUDGE
    fin(2700);
    fout(2700);
    #endif

    scanf("%d%d",&n,&k);
    rep(i,1,n)
        fa[i] = i;
    rep(i,1,k){
        int point;
        scanf("%d",&point);
        p[point] = 1;
    }

    Rep(i,1,n){
        scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
        ans += e[i].w;
    }

    sort(e + 1,e + n + 1,cmp);
    kruskal();

    printf("%lld",ans);

    return 0;
}