AT3978 题解

题目传送门

小学生又双叒叕来写题解啦！

这题的题面有误，讨论区有人提出来了，望管理员修改一下。

我就不发正确的题目描述了，自己去讨论区看看。

---

不说闲话，我看到题目的第一反应是：直接模拟不就好了！

于是写出了如下代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#define N (int)(1e5 + 5)
using namespace std;
int n, a[N]; 
int dis(int x)  //表示不用去第 x 个点的最短路程。 
{
	int ans = 0, now = 0;  //分别记录答案与当前位置。 
	for (int i = 1; i <= n+1; i++) 
	//看到 i 的范围了吗，由于第 (n+1) 个是零，我们直接遍历到那里，不就相当于回到零号点了吗？ 
	{
		if (i == x) continue;
		ans += (abs(now - a[i]));
		now = a[i];
	}
	return ans;
}
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= n; i++) printf("%d\n", dis(i));  //勿忘祖传换行。 
	return 0;
}

然而第一个点就爆掉了，原因是超时。

超时的原因很简单，就是这份代码的时间复杂度是 \(O(n^2)\) 这么大，不爆才怪呢！

因此，我们可以预处理。

准确的说，由于每次计算最短路程是相关的，所以思考：能否通过整体的一次计算来得到所有答案呢？

答案是可以的。

首先算出完整路程，也就是没有点被省略时的路程。

然后，假设第 \(i\) 个点不用去，那么只需在完整路程中减去一些东西就是结果了。

具体看这两张图。

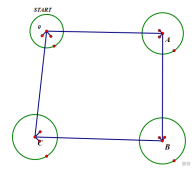
如果省略第一个点，就会变成下图。

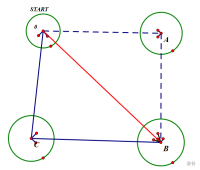
代码也就水到渠成了。

送上满分代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#define N (int)(1e5 + 5)
using namespace std;
int n, a[N]; 
int dis()  //表示最短路程。 
{
	int ans = 0, now = 0;  //分别记录答案与当前位置。 
	for (int i = 1; i <= n+1; i++) 
	//看到 i 的范围了吗，由于第 (n+1) 个是零，我们直接遍历到那里，不就相当于回到零号点了吗？ 
	{
		ans += (abs(now - a[i]));
		now = a[i];
	}
	return ans;
}
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	int s = dis();
	for (int i = 1; i <= n; i++) 
	{
		//关于下面重点代码的解析，图内都标好了，对着图模拟即可。 
		int t1 = abs(a[i] - a[i-1]);
		int t2 = abs(a[i] - a[i+1]);
		int t3 = abs(a[i-1] - a[i+1]);
		printf("%d\n", s - t1 - t2 + t3);  //勿忘祖传换行。 
	}
	return 0;
}

首发：2022-02-06 19:15:58

标签：路程,int,题解,代码,AT3978,答案,include
来源： https://www.cnblogs.com/liangbowen/p/16622807.html