[九省联考 2018] 一双木棋 chess

题目描述

菲菲和牛牛在一块 \(n\) 行 \(m\) 列的棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。

棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。

落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

棋盘的每个格子上，都写有两个非负整数，从上到下第 \(i\) 行中从左到右第 \(j\) 列的格子上的两个整数记作 \(a_{i,j}\) 和 \(b_{i,j}\)。

在游戏结束后，菲菲和牛牛会分别计算自己的得分：菲菲的得分是所有有黑棋的格子上的 \(a_{i,j}\) 之和，牛牛的得分是所有有白棋的格子上的 \(b_{i,j}\) 的和。

菲菲和牛牛都希望，自己的得分减去对方的得分得到的结果最大。现在他们想知道，在给定的棋盘上，如果双方都采用最优策略且知道对方会采用最优策略，那么，最终的结果如何？

\(1 \leq n, m \leq 10\)，\(0 \leq a_{i, j}, b_{i, j} \leq 10^5\)。

Solution

首先可以写一手对抗搜索，写得好加剪枝可能可以过掉。

回到正解。注意到任意时候场上填了的棋子必定都成一条从左下角往右上角走的路径。这条路径有 \(n+m-1\) 个转角，每个转角只会有两种方向：向右或向上。

考虑状压，设向上为 1，向右为 0。则下图可表示为：010010101。

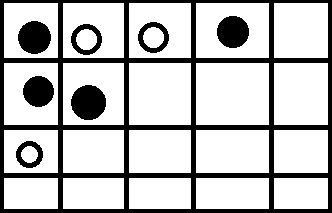
思考每次放棋子会对状态进行怎样的更改。发现一个位置能放棋子，其在状态中必定对应着 01，而在这个位置放了棋子后，01 会变成 10。

比如说上图，若在第二行第三列放棋子，则状态变成：010100101。

转移的时候，处理出哪些位置可以放棋子，然后再根据当前的下棋人转移即可。

ps:用记忆化搜索就处理出当前状态的下棋人是谁，直接在搜索的时候记录一下就好。

Code

#include<cstdio>
#include<algorithm>
#define N 11
#define inf 2147483647
using namespace std;
int n,m,a[N][N],b[N][N],f[1<<(N<<1)];
bool bj[1<<(N<<1)];
int dfs(int s,int p)
{
	if (bj[s]) return f[s];
	f[s]=p?-inf:inf;
	int x=n+1,y=1; 
	for (int i=0;i<n+m-1;++i)
	{
		if (s&(1<<i)) --x;
		else ++y;
		if ((s&(3<<i))!=(1<<i)) continue;
		int ss=s^(3<<i);
		if (p) f[s]=max(f[s],dfs(ss,0)+a[x][y]);
		else f[s]=min(f[s],dfs(ss,1)-b[x][y]);
	}
	bj[s]=true;
	return f[s];
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;++i)
		for (int j=1;j<=m;++j)
			scanf("%d",&a[i][j]);
	for (int i=1;i<=n;++i)
		for (int j=1;j<=m;++j)
			scanf("%d",&b[i][j]);
	bj[((1<<n)-1)<<m]=true;
	printf("%d\n",dfs((1<<n)-1,1));
	return 0;
}

标签：得分,菲菲,格子,leq,木棋,棋子,九省,棋盘,联考
来源： https://www.cnblogs.com/Livingston/p/16599977.html