骗我呢
作者:互联网
题意:
求有多少个 \(n × m\) 的矩阵满足
- \(0\) \(≤\) \(a_i,_j\) \(≤\) \(m\)
- \(a_{i,j}\) \(<\) \(a_{i,j + 1}\)
- \(a_{i,j}\) \(<\) \(a_{i-1, j + 1}\)
首先观察到 \(a_{i,j}\) 的取值范围以及矩阵的列,得出矩阵的每一行必然有一个在 \(0\) ~ \(m\) 之间的数是不存在的。
通过第二个矩阵需要满足的条件得出每一行除去这个不存在的数,这个序列是单调递增的。
设第 \(i\) 行这个不存在的数为 \(b_{i}\),那么看看 \(b_i\) 与 \(a_{i, j}\) 的关系。
根据矩阵每一行单调递增的性质,不难得出:
\(a_{i, j}\) \(=\) \(j\) \(-\) \(1\) \(+\) \([\) \(b_i\) \(≤\) \(j\) \(]\);
再将这个式子代入矩阵需要满足的第三个条件得出:
\(j\) \(-\) \(1\) \(+\) \([\) \(b_i\) \(≤\) \(j\) \(]\) \(<\) \(j\) \(+\) \(1\) \(-\) \(1\) \(+\) \([\) \(b_{i - 1}\) \(≤\) \(j\) \(+\) \(1\) \(]\);
化简可得:
\([\) \(b_i\) \(≤\) \(j\) \(]\) \(<\) \(1\) \(+\) \([\) \(b_{i - 1}\) \(≤\) \(j\) \(+\) \(1\) \(]\);
因此可以知道:
当 \(b_i\) \(≤\) \(j\) 成立时 \(b_{i - 1}\) \(≤\) \(j\) \(+\) \(1\) 一定也成立。
进而可得:
\(b_i\) \(≥\) \(b_{i - 1}\) \(-\) \(1\);
得出这个关系后,我们设 \(f_{i, j}\) 表示第 \(i\) 行中值为 \(j\) 的数不存在所能构成的矩阵的个数。
根据上面 \(b_i\) 和 \(b_{i-1}\) 的关系式,不难得出 \(f_{i,j}\) 的转移方程:
\(f_{i,j}\) \(=\) \(\sum_{k = 0}^{j + 1}\) \(f_{i-1, k}\);
将这个方程展开化简得出:
\(f_{i, j}\) \(=\) \(f_{i, j - 1}\) \(+\) \(f_{i - 1, j + 1}\);
边界条件:
\(f_{i, 0}\) \(=\) \(f_{i - 1, 0}\) \(+\) \(f_{i - 1, 1}\);
根据上面的最开始得出的转移方程可以知道最终答案就是 \(f_{n + 1, m - 1}\)
将转移式子转化为一张图可得:
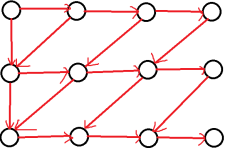
发现图的左边与中间并不整齐,因此再转化:
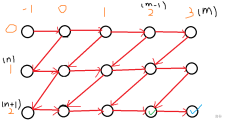
因此此题此时转化为了从左上角的 \((0,\) \(-1)\) 号点,每次可以向左下或者向右走,不能走出图的边界,走到画绿挑的点 \((2,\) \(2)\) 号点(到蓝挑点也一样)的方案数。
首先只有向左下走一种方法可以到达下一层,而我们一共需要下 \(n\) 层,因此向左下走的步数就为 \(n\),且这样走一定不会越出矩阵下面或上面的边界。
此时也相当于我们一共向左也走了 \(n\) 步,而为了到达右端的 \(m\) \(-\) \(1\) 点,我们还需要向右走 \(n\) \(+\) \(m\) 步,因此问题再次转化为:
在一个数轴上,从 \(-1\) 出发,向左走 \(n\) 步,向右走 \(n\) \(+\) \(m\) 步,不越过 \([\) \(-1,\) \(m\) \(]\) 这个范围,求方案数。
为了方便,将整体向右平移一位,问题最终变为:
在一个数轴上,从原点出发,向左走 \(n\) 步,向右走 \(n\) \(+\) \(m\) 步,不越过 \([\) \(0,\) \(m\) \(+\) \(1\) \(]\) 这个范围,求方案数。
考虑采用反射的方法,以点 \(-1\) 为中心对称,以 \(m\) \(+\) \(2\) 为中心进行对称,而这个方法的基础可以在 这道题 学习。
相较于普通的采用反射法的题来说,此题最大的不同就是需要进行反复容斥,即我们不仅需要求出越过原点的方案数,还需要求出先越过 \(m\) \(+\) \(1\) 再越过原点的方案数,再就还需要求出先越过原点再越过 \(m\) \(+\) \(1\) 再越过原点的方案数,因此可以递归求解。
以先横跨左端点为例:
设 \(crossL(l,\) \(r,\) \(end)\) 表示当前经过若干次反射得到的限制区间为 \(l\) ~ \(r\),需要到达的终点为 \(end\),的方案数。
那么它的返回值就是从 \(0\) 到 \(end\) 走 \(2n\) \(+\) \(m\) 步的方案数 \(-\) 再跨一遍左(右)区间的方案数。
设向左走 \(a\) 步,向右走 \(b\) 步到达 \(end\)(这里 \(a\),\(b\) 是啥都无所谓)
那么可得方程:
\(\begin{cases}a+b=2n + m\\ a-b=end\\ \end{cases}\)
解得
\(a\) \(=\) \(n\) \(+\) \(\frac{m + end}{2}\);
所以总的方案数就为 \(C(n\) \(+\) \(\frac{m + end}{2},\) \(2n\) \(+\) \(m)\);
当然还需要减去 \(crossL(2\) \(\times\) \((l\) \(-\) \(1)\) \(-\) \(r,\) \(2\) \(\times\) \((l\) \(-\) \(1)\) \(-\) \(l,\) \(2\) \(\times\) \((l\) \(-\) \(1)\) \(-\) \(end)\)。这是因为对于每一次反射,区间左端点就变为了右端点,右端点就变为了左端点,因此我们只需不断的按照当前的左端点进行反射即可。
具体见 code:
#include <cstdio>
#include <cmath>
typedef long long ll;
const int MAXN = 1e6;
const ll MOD = 1e9 + 7;
ll n, m;
ll fac[3 * MAXN + 10], invFac[3 * MAXN + 10];
ll quickPow(ll x, ll k) {
ll ans = 1ll;
while(k) {
if(k & 1) {
ans = ans * x % MOD;
}
k >>= 1;
x = x * x % MOD;
}
return ans;
}
ll C(ll mm, ll nn) {
return fac[nn] * invFac[mm] % MOD * invFac[nn - mm] % MOD;
}
ll crossR(ll l, ll r, ll end) {
if(abs(end) > 2 * n + m) return 0ll; //判断终点能否到达
return (C(n + ((m + end) >> 1), 2 * n + m) - crossR(2 * (r + 1) - r, 2 * (r + 1) - l, 2 * (r + 1) - end)) % MOD;
}
ll crossL(ll l, ll r, ll end) {
if(abs(end) > 2 * n + m) return 0ll;
return (C(n + ((m + end) >> 1), 2 * n + m) - crossL(2 * (l - 1) - r, 2 * (l - 1) - l, 2 * (l - 1) - end)) % MOD;
}
int main() {
scanf("%lld %lld", &n, &m);
fac[0] = 1ll, invFac[0] = 1ll;
fac[1] = 1ll, invFac[1] = 1ll;
for(int i = 2; i <= 2 * n + m; ++i) { //求阶乘和其逆元,以便于 O(1) 计算组合数
fac[i] = fac[i - 1] * i % MOD;
invFac[i] = quickPow(fac[i], MOD - 2);
}
ll ans = ((crossR(0, m + 1, m) + crossL(0, m + 1, m)) % MOD - C(n + m, 2 * n + m)) % MOD; //第一次横跨L和R把中间这一段算了两遍,因此要再减一下
printf("%lld\n", (ans + MOD) % MOD);
return 0;
}
标签:,end,ll,矩阵,端点,return,MOD 来源: https://www.cnblogs.com/louis660/p/16586016.html