【ACM】dp专场训练
作者:互联网
A.摘花生
题目描述
Hello Kitty想摘点花生送给她喜欢的米老鼠。
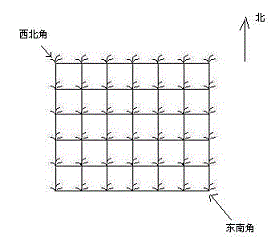
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1 ≤ T ≤ 100,
1 ≤ R,C ≤ 100,
0 ≤ M ≤ 1000
输入样例:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例:
8
16
思路
<闫氏dp分析法>
状态表示:在第i行第j列最多摘到的花生数为f[i][j]
状态计算:f[i][j] = f[i][j] + max(f[i-1][j] , f[i][j-1])

C++ 代码
#include <bits/stdc++.h>
#pragma GCC optimize(2)//O(2)优化
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
const int N = 110;
int f[N][N];
void solve()
{
int r , c;
cin >> r >> c;
for(int i = 1;i <= r;i ++)
{
for(int j = 1;j <= c;j ++)
{
int x;
cin >> x;
f[i][j] = x;
}
}
for(int i = 1;i <= r;i ++)
{
for(int j = 1;j <= c;j ++)
{
f[i][j] += max(f[i-1][j], f[i][j-1]);
}
}
// cout << "ans=";
cout << f[r][c] << endl;
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T --)
solve();
return 0;
}
B.合唱队形
题目描述
N 位同学站成一排,音乐老师要请其中的 (N-K) 位同学出列,使得剩下的 K 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 K 位同学从左到右依次编号为 1,2…,K,他们的身高分别为 T\_1,T\_2,…,T\_K, 则他们的身高满足 T\_1 < … < T\_i > T\_{i+1} > … > T\_K(1 ≤ i ≤ K)。
你的任务是,已知所有 N 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入格式
输入的第一行是一个整数 N,表示同学的总数。
第二行有 N 个整数,用空格分隔,第 i 个整数 T\_i 是第 i 位同学的身高(厘米)。
输出格式
输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。
数据范围
2 ≤ N ≤ 100,
130 ≤ T[i] ≤ 230
输入样例:
8
186 186 150 200 160 130 197 220
输出样例:
4
思路
C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
const int N = 110;
int n ;
int f[N] , g[N];
int h[N];
void solve()
{
cin >> n;
for(int i = 1;i <= n;i ++)
cin >> h[i];
for(int i = 1;i <= n;i ++)
{
f[i] = 1;
for(int j = 1;j < i;j ++)
{
if(h[j] < h[i])
f[i] = max(f[i] , f[j] + 1);
}
}
for(int i = n;i > 0 ;i --)
{
g[i] = 1;
for(int j = n;j > i;j --)
{
if(h[j] < h[i])
g[i] = max(g[i] , g[j] + 1);
}
}
int res = 0;
for(int i = 1;i <= n;i ++)
res = max(res,f[i]+g[i]-1);
cout << n-res << endl;
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
T = 1;
//cin >> T;
while(T --)
solve();
return 0;
}
C.采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。
为此,他想拜附近最有威望的医师为师。
医师为了判断他的资质,给他出了一个难题。
医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
输入文件的第一行有两个整数 T 和 M,用一个空格隔开,T 代表总共能够用来采药的时间,M 代表山洞里的草药的数目。
接下来的 M 行每行包括两个在 1 到 100 之间(包括 1 和 100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出文件包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
数据范围
1 ≤ T ≤ 1000,
1 ≤ M ≤ 100
输入样例:
70 3
71 100
69 1
1 2
输出样例:
3
思路
与01背包问题一样,
区别:时间 --> 背包容量
状态表示:所有只从前i个物品中选,且总时间不超过j的选法
状态计算:f[i][j] = max(f[i][j] , f[i-1][j-v[i]]+w[i])

C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
const int N = 1010;
int n , m;
int t[N] , v[N];
int f[N][N];
void solve()
{
cin >> m >> n;
for(int i = 1;i <= n;i ++)
cin >> t[i] >> v[i];
for(int i = 1;i <= n;i ++)
{
for(int j = 0;j <= m;j ++)
{
f[i][j] = f[i-1][j];
if(j >= t[i])
f[i][j] = max(f[i][j] , f[i-1][j-t[i]]+v[i]);
}
}
cout << f[n][m] << endl;
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
T = 1;
//cin >> T;
while(T --)
solve();
return 0;
}
D.开心的金明
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 N 元钱就行”。
今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的 N 元。
于是,他把每件物品规定了一个重要度,分为 5 等:用整数 1 \\sim 5 表示,第 5 等最重要。
他还从因特网上查到了每件物品的价格(都是整数元)。
他希望在不超过 N 元(可以等于 N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j 件物品的价格为 v\[j\],重要度为 w\[j\],共选中了 k 件物品,编号依次为 j\_1,j\_2,…,j\_k,则所求的总和为:
v\[j\_1\] \\times w\[j\_1\]+v\[j\_2\] \\times w\[j\_2\]+…+v\[j\_k\] \\times w\[j\_k\]
请你帮助金明设计一个满足要求的购物单。
输入格式
输入文件的第 1 行,为两个正整数 N 和 m,用一个空格隔开。(其中 N 表示总钱数,m 为希望购买物品的个数)
从第 2 行到第 m+1 行,第 j 行给出了编号为 j-1 的物品的基本数据,每行有 2 个非负整数 v 和 p。(其中 v 表示该物品的价格,p 表示该物品的重要度)
输出格式
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(数据保证结果不超过 10^8)。
数据范围
1 ≤ N < 30000,
1 ≤ m < 25,
0 ≤ v ≤ 10000,
1 ≤ p ≤ 5
输入样例:
1000 5
800 2
400 5
300 5
400 3
200 2
输出样例:
3900
思路
类似于01背包问题
状态表示:从1到i中选,且总体积不超过j的所有选法的集合
状态计算:f[i][j] = max(f[i][j] , f[i][j-v[i]]+w[i])

C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
const int N = 35;
const int M = 30010;
int n , m;
int f[N][M];
void solve()
{
cin >> m >> n;
for(int i = 1;i <= n;i ++)
{
int v , w;
cin >> v >> w;
w = v * w;
for(int j = 0;j <= m;j ++)
{
f[i][j] = f[i - 1][j];
if(j >= v)
f[i][j] = max(f[i][j] , f[i-1][j-v]+w);
}
}
cout << f[n][m] << endl;
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
//cin >> T;
T = 1;
while(T --)
solve();
return 0;
}
E.空心菱形
题目藐视
输入一个整数 n,输出一个空心菱形,其中每个边由 n 个'*'组成。
输入格式
输入包含一个整数 n。
输出格式
输出一个空心菱形,每个边由 n 个'*'组成 。
数据范围
1≤n≤20。
思路
模拟(不知道dp思路)
代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
int n;
void solve()
{
cin >> n;
//上半部分
for(int i = 1;i <= n;i ++)
{
int k = n - i;
while(k --)
printf(" ");
if(i == 1)
printf("*");
else
{
printf("*");
int k = 2 * i - 3;
while(k --)
printf(" ");
printf("*");
}
printf("\n");
}
//下半部分
for(int i = n - 1;i >= 1;i --)
{
int k = n - i;
while(k --)
printf(" ");
if(i == 1)
printf("*");
else
{
printf("*");
int k = 2 * i - 3;
while(k --)
printf(" ");
printf("*");
}
printf("\n");
}
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
//cin >> T;
T = 1;
while(T --)
solve();
return 0;
}
F.大盗阿福
题目描述
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T (T≤50) ,表示一共有 T 组数据。
接下来的每组数据,第一行是一个整数 N(1≤N≤100,000),表示一共有 N 家店铺。
第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过 1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
提示
对于第一组样例,阿福选择第 2 家店铺行窃,获得的现金数量为 8。对于第二组样例,阿福选择第 1 和 4 家店铺行窃,获得的现金数量为 10+14=24。
样例输入
2
3
1 8 2
4
10 7 6 14
样例输出
8
24
思路
状态表示:前i家店铺的最大金额
状态计算:f[i] = max(f[i-1] , f[i-2]+a[i])

代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
typedef unsigned long long ull;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1e9+7;
int dx[] = {0,1,0,-1};
int dy[] = {-1,0,1,0};
const int N = 100010;
int a[N] , f[N];
int n;
void solve()
{
cin >> n;
for(int i = 1;i <= n;i ++)
cin >> a[i];
for(int i = 1;i <= n;i ++)
f[i] = max(f[i-1] , f[i-2] + a[i]);
// cout << "ans = " ;
cout << f[n] << endl;
}
int main()
{
/*读入优化*/
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T --)
solve();
return 0;
}
标签:专场,typedef,const,int,样例,long,--,ACM,dp 来源: https://www.cnblogs.com/heystar/p/16566539.html
