虚树学习笔记
作者:互联网
「虚树」学习笔记
\(\mathcal{Part.1}\) \(\texttt{引子}\)
P2495 [SDOI2011] 消耗战:给定 \(n\) 个点的树,边有边权,\(m\) 次询问,每次给定 \(k_i\) 个点,问最少要炸毁多少条边,使得 \(1\) 不能到达任何一个给定的点。\(1\le n\le 2.5\times 10^5\),\(1\le m\le 10^5\)。
\(\Theta(nm)\) 做法每次对树爆搜即可。
但实际上我们不需要对每一个点都搜一遍。比如对于一条链,上面全是非特殊点,就没有必要全部算一遍。
这就引入了「虚树」这一概念,我们考虑将那些不重要的边都扔掉,不改变树的形态,而又保留最少的点。

如果我们将 \(1\to 2\) 这一条链所称一条边,那么这样建树是无法满足的,因为 \(3\) 需要连到一个点上。
所以可以将 \(1\to 4,2\to 4,3\to 4\) 都缩成一条边,建出新树。
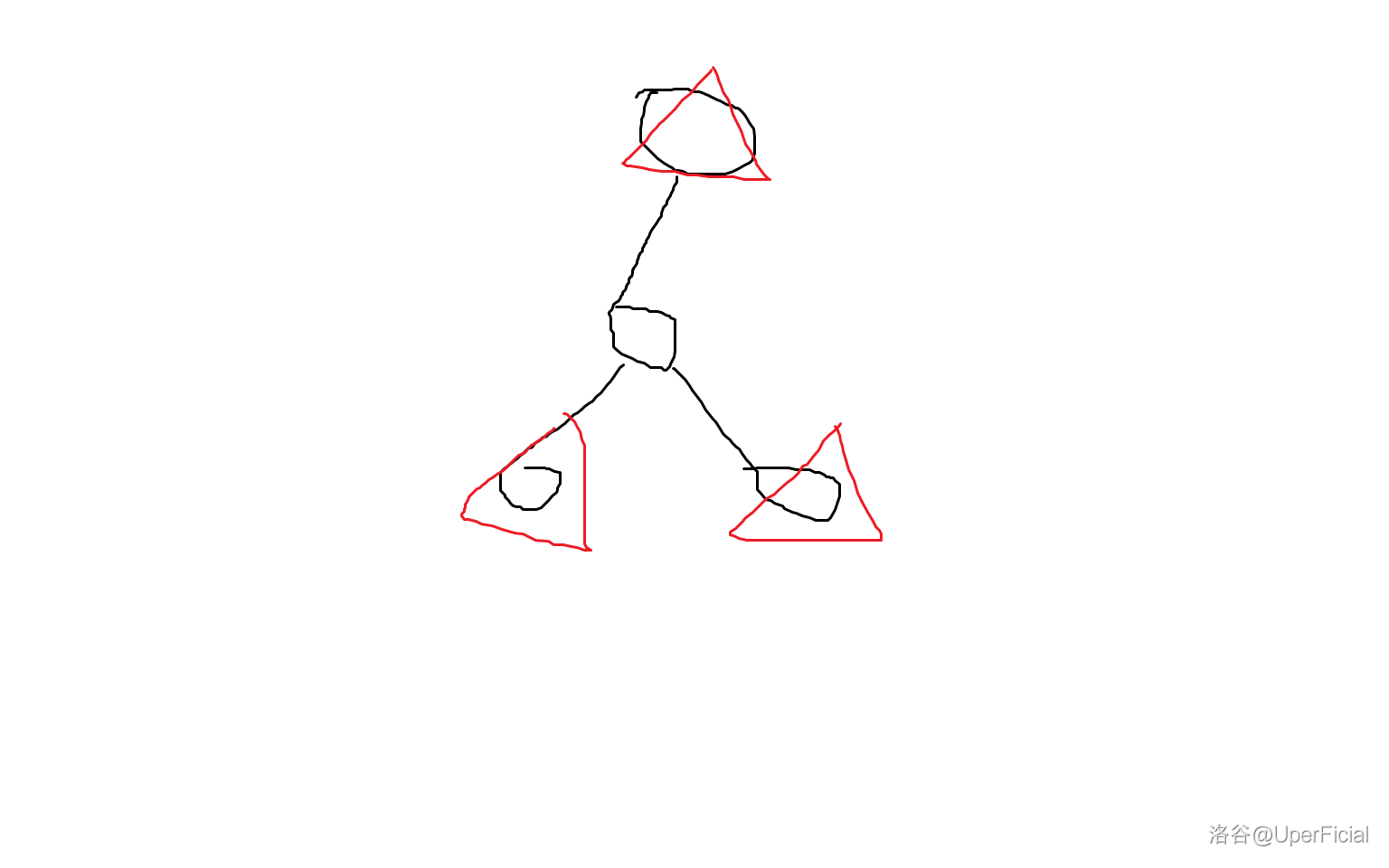
这就是上图的所建出的「虚树」。
我们称虚树中的点为关键点。
\(\mathcal{Part.2}\) \(\texttt{建树}\)
假设说我们有这么一棵树:
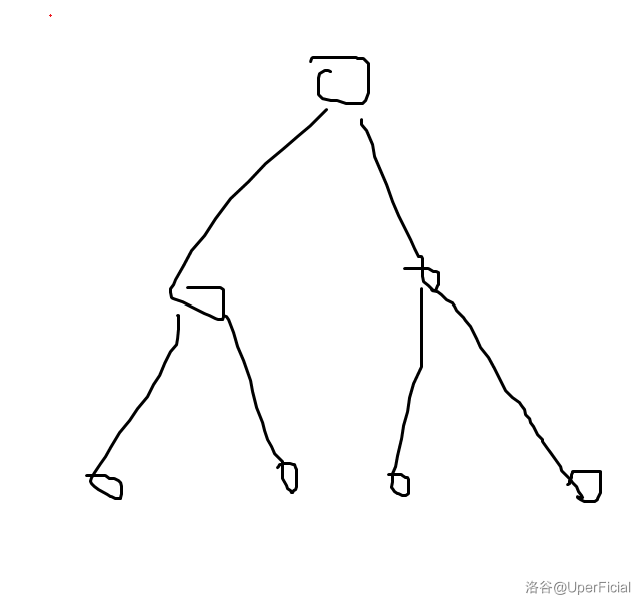
下面列举选取不同关键点时所得到的虚树:
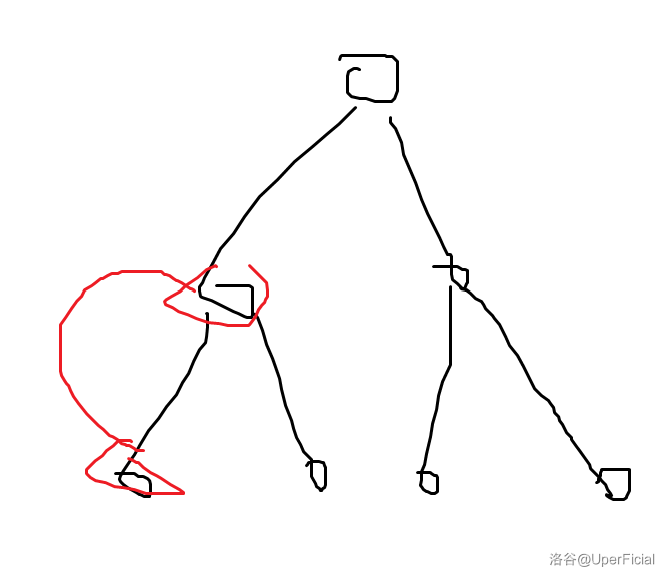
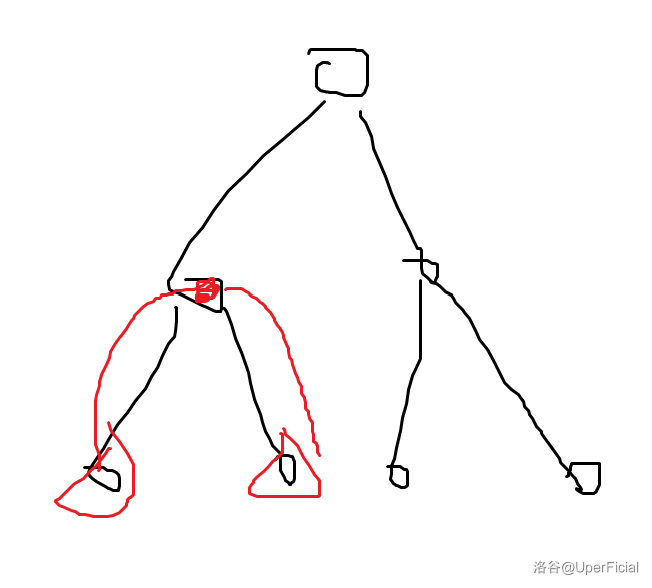

发现任意两个特殊点的 \(\text{LCA}\) 都需要被加入虚树中,但这样暴力加点是 \(\Theta(k^2)\) 的。但是我们可以对每一个特殊点的 \(\text{dfn}\) 从小到大排序,相邻两个点的 \(\text{LCA}\) 就都包括在内了。
这里提供一个非常简单的做法:
- 求每一个特殊点的 \(\text{dfn}\) 后排序。
- 求相邻两个点的 \(\text{LCA}\) 并判重。
- 根据祖先关系建树。
根据祖先关系进行建树的具体过程为,对于去重并排序后的相邻两点 \(x_i,x_{i+1}\),我们可以求出它们的 \(\texttt{LCA}\),记为 \(d\),那么我们即可知道,\(d\) 在虚树上肯定是 \(x_{i+1}\) 的父亲。
证明也很简单。首先我们知道,在 \(rt\to x_{i+1}\) 这一条路径上不会有点了,因为我们是按照 \(\text{dfn}\) 值进行排序的。假设 \(d\) 不是 \(x_{i+1}\) 的父亲,那么 \(x_{i+1}\) 的父亲 \(fa\) 肯定会在这一条路径上。如果 \(fa\) 是 \(d\) 的祖先,那么 \(x_i\) 就无从连边。如果 \(fa\) 是 \(d\) 的后代,那么 \(x_i\) 这个点只能向 \(d\) 连边,而我们知道 \(d\) 和 \(fa\) 都不是关键点,所以它们可以合成一个点,也就是 \(d\)。
代码也非常好写,关键比单调栈的做法好理解。
inline void build(int k)//给定 k 个关键点 vir1,vir2,...,virk
{
int num=k;
sort(vir+1,vir+1+k,cmp);
rep(i,2,k)
{
int g=lca(vir[i],vir[i-1]);
if(g!=vir[i]&&g!=vir[i-1]) vir[++num]=g;
}
sort(vir+1,vir+1+num);
num=unique(vir+1,vir+1+num)-vir-1;//去重
sort(vir+1,vir+1+num,cmp);//注意这里需要按照 cmp 再次排序
rep(i,2,num)
{
int g=lca(vir[i],vir[i-1]);
G[g].push_back(vir[i]);//连边
}
return;
}
\(\texttt{P2495 [SDOI2011] 消耗战}\)
再回来这道题,我们建出虚树后,在上面进行 \(\texttt{DP}\)。
设 \(f_i\) 表示以 \(i\) 为根的子树中,要使所有的点特殊点都不能到达 \(1\) 号点,最少的花费。设 \(t_i\) 表示 \(1\to i\) 路径上的最小边权。
对于当前节点 \(u\),如果它是特殊点,那么我们只能断掉 \(1\to u\) 路径上的一条边,贪心考虑,我们断掉边权最小的一条边,即 \(t_u\)。如果它不是特殊点,我们既可以断掉 \(1\to u\) 边权最小的一条边,也可以让 \(u\) 的每个儿子的子树都不能到达 \(1\),即 \(f_u\leftarrow \min(t_u,\sum_{v\in \operatorname{son}(u)}f_v)\)。
本题得以解决。
标签:vir,text,texttt,笔记,我们,学习,num,虚树 来源: https://www.cnblogs.com/UperFicial/p/16546969.html