高尔顿钉板的统计意义—R实现

提到高尔顿，人们总是把他和钉板实验联系在一起，偶尔也会有人提及他是达尔文的表弟。实际上，作为维多利亚时代的人类学家、统计学家、心理学家和遗传学家，同时又是热带探险家、地理学家、发明家、气象学家，高尔顿简直就是一位集大成者。高尔顿钉板是一个关于概率的模型，小球每次下落，将随机的向两边等概率的下落，当有大量的小球都滚下时，最终在钉板下面不同位置收集到的小球数量，将符合二项分布概率。出于直观表示模拟实现高尔顿钉板的概率模型。

一、 高尔顿钉板和二项分布

先来说明共n层（最下方有n+1格）的高尔顿板中小球的分布满足二项分布 $$B(n,\frac{1}{2})$$。

二、 二项分布的正态渐进

经过以上铺垫，我们终于进入了正题：用二项分布近似正态分布。我们知道，二项分布是离散的分布，正态分布是连续的分布，两者如何联系起来？
这里我们直接讨论一般的二项分布$$B(n,p)$$,高尔顿板的情况只需令 $$p=\frac{1}{2}$$ 即可。先看动图：

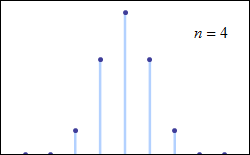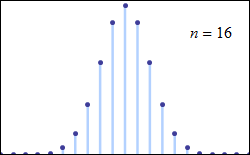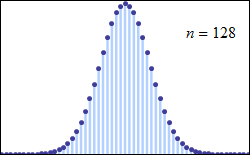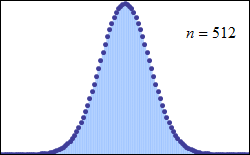
正态分布在数据分析中扮演了非常重要的角色，它代表了系统的稳定特征，它是自然环境和人类社会中最常见的数据分布形式。除此之外，在某些情况下，正态分布还能够用来近似其他的数据概率分布类型，比如二项分布和泊松分布，这也说明了正态分布使用的范围和重要性。在一定条件下，正态分布是二项分布的一个良好近似，可用于计算二项分布的概率。由于这样得到的概率只是对二项分布真实概率值的近似，所以正态分布的这种应用被称为二项分布的正态近似。

回顾正态分布曲线的形态，表现为对称的倒置钟形，因此只有二项分布的形态近似对称的倒置钟形，使用正态分布近似二项分布才是合适的。从二项分布的理论及其概率质量函数入手，我们可以很容易地总结出使二项分布近似正态分布的两个条件。“成功”的概率用字母p表示，值越接近0.5，即“成功”结果出现的概率与“失败”概率越接近，二项分布将越对称。如下图所示，保持伯努利试验（一次试验只有两种结果）的次数n不变，随着成功概率p逐渐增加到0.5，二项分布逐渐对称，近似于均值为np、方差为npq的正态分布。对任意“成功”概率p ，无论其距离0.5有多远，随着试验次数n的增加，得到的二项分布与均值为np、方差为npq的正态分布越来越接近。如下图所示，保持“成功”的概率p=0.1不变，分别做伯努利试验次数等于10、25和100的二项分布图，对比后可以发现，二项分布图从最初的右偏分布逐渐对称，当试验次数等于100时，二项分布几乎与正态分布一致。

由于试验次数和“成功”概率都能使二项分布近似于正态分布，那么这两个条件达到什么标准时，二项分布和正态分布才能近似，它们的概率计算结果才能互相替代呢？因为每个分析者对于偏差的接受程度不同，所以对于这个问题，没有一个统一的标准，不过，在数据分析领域，有一个普遍能够接受的最低限度，那就是当np和nq两者的计算结果都大于或等于5时，通过二项分布概率质量函数计算得到的概率值与正态分布概率密度函数积分得到的概率值的误差就小到能够被接受。更严格一点，就是要求np>5且nq>5，两者之间的误差就更小了。

三、高尔顿钉板的R实现

d<- NA
for(i in 1:5000)
  {a=rbinom(30,1,0.7)
  b=sum(a)
  d=c(d,(b-10))
}
hist(d)

四、总结

中心极限定理在生活中有重要的应用。高尔顿板实验中，小球每掉落一层，都有可能向左或是向右，这些因素左右这小球最终的落点。同样的，自然界中许多随机现象都有各种各样的干扰因素，影响着一个事件可能的分布，但是在这些因素的叠加影响之下，只要样本数量足够多，这些随机现象往往就会遵循正态分布。这也是一种数学之美吧！

参考文献

1.(高尔顿板：从混乱到秩序 )[https://www.sohu.com/a/234859732_616676]
2.(统计学中统计规律 )[https://www.wenmi.com/article/pu8xw704z9ru.html]
3.(为什么高尔顿板可以模拟正态分布？)[https://zhuanlan.zhihu.com/p/518115021]
4.(用Python模拟高尔顿钉板实验 )[https://blog.csdn.net/xufive/article/details/121115824]

标签：概率,钉板,高尔顿,近似,二项分布,正态分布,统计
来源： https://www.cnblogs.com/haohai9309/p/16522445.html