dp专题

2022-07-27 19:05:28 作者：互联网

P1280 尼克的任务

链接：https://www.luogu.com.cn/problem/P1280

本题的关键在于顺推不好做想着要倒推想着要统计开始的时间点排序是为了消除后效性！！！！是个非常好的模型

#include<iostream>  
#include<algorithm>  
using namespace std;  
long int n,k,sum[10001],num=1,f[10001];  
struct ren//结构体，一起排序 ，从大到小   
{  
    long int ks,js;  
};  
ren z[10001];  
int cmp(ren a,ren b)  
{  
    return a.ks>b.ks;  
}  
int main()  
{  
    long int i,j;   
    cin>>n>>k;  
    for(i=1;i<=k;i++)  
    {  
    cin>>z[i].ks>>z[i].js;    
    sum[z[i].ks]++;  
    }  
    sort(z+1,z+k+1,cmp);  
    for(i=n;i>=1;i--)//倒着搜   
    {  
        if(sum[i]==0)  
        f[i]=f[i+1]+1;  
        else for(j=1;j<=sum[i];j++)  
        {  
            if(f[i+z[num].js]>f[i])  
            f[i]=f[i+z[num].js];  
            num++;//当前已扫过的任务数   
        }  
    }  
    cout<<f[1]<<endl;  
}

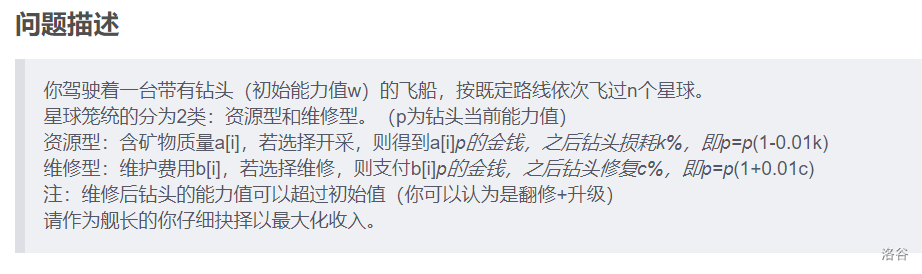
这个题目和费用提前算不太一样两者本质上都是消除后效性

这个题不同的就是不知道后面到底哪些要选而费用提前算是后面的一定都是会选的

所以这个题巧妙地从后往前转移这样转移前面的一定是后面最优策略转移方程非常像算期望值

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 100005
double f[maxn];
double n,k,c,w;
int a[maxn],b[maxn];
int main()
{
    int i;
    scanf("%lf%lf%lf%lf",&n,&k,&c,&w);
    for(i=1;i<=n;i++) scanf("%d%d",&a[i],&b[i]);
    for(i=n;i>=1;i--)
    {
        if(a[i]==1) f[i]=max(f[i+1],f[i+1]*(1-k/100)+b[i]);
        if(a[i]==2) f[i]=max(f[i+1],f[i+1]*(1+c/100)-b[i]);
    }
    printf("%.2lf",f[1]*w);
}

这个dp以前没见过确实不会怎么才能保证两两互不相交呢在我印象里面没有这样操作过的dp

考虑换个想法设dp[i,j,k]表示前i个两者差值为j 用了k次加倍因为下标不能为负所以整体向右偏移1300

初始化 dp[0,1300,0]=0 答案 max{dp[n,1300,i]} i属于[0,k]

转移方程：dp[i,j,k]=max(dp[i-1,j+v[i],k]+w[i],dp[i-1,j-v[i],k]+w[i],dp[i-1,j+2v[i],k-1]+w[i],dp[i-1,j-2v[i],k-1]+w[i])

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int N=103;
typedef long long ll;
ll f[N][3003][N],w[N],v[N];
int main()
{
	memset(f,-0x3f,sizeof f);
	f[0][1300][0]=0;
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		scanf("%lld%lld",&w[i],&v[i]);
	for(int i=1;i<=n;i++)
	for(int j=0;j<=m;j++)
	for(int k=0;k<=2600;k++)
	{
		f[i][k][j]=f[i-1][k][j];
		if(k>=2*v[i]&&j>=1)
			f[i][k][j]=max(f[i][k][j],f[i-1][k-2*v[i]][j-1]+w[i]);
		if(k>=v[i])
			f[i][k][j]=max(f[i][k][j],f[i-1][k-v[i]][j]+w[i]);
		if(k+2*v[i]<=2600&&j>=1)
			f[i][k][j]=max(f[i][k][j],f[i-1][k+2*v[i]][j-1]+w[i]);
		if(k+v[i]<=2600)
			f[i][k][j]=max(f[i][k][j],f[i-1][k+v[i]][j]+w[i]);
	}
	ll ans=-0x3f3f3f3f;
	for(int i=0;i<=m;i++)
		ans=max(ans,f[n][1300][i]);
	cout<<ans;
	return 0;
}

https://www.luogu.org/problem/P2577

分析:

首先本题不是贪心排序就是dp

再数据范围<=200,就只有可能是dp了

考虑本题,容易想到应该尽量让那些打饭快却吃饭慢的排在前面

又因为所有人打饭的总时间是一定的,

即无论怎么安排所有人打完饭都会耗费这么多时间

所以我们只用考虑吃饭慢的排在前面则一定是最优的

但此时有两个窗口,怎样安排就要dp了

用f[i,j]记录前i个人排队，第一队用时为j的情况下最大用时。
不记录第2队状态的原因是可以由第一队状态推出来。
为了便于计算，建议使用前缀和维护一下，可以较为简易的计算出第2队的情况。
那么我们就得到了这样个方程：

加入第一队的情况下： f[i,j]=min(f[i,j],max(f[i-1,j-a[i].x],j+a[i].y));

当前最小时间为上一个人用的时间和这一个人用的时间的最大值

加入第二队同理

f[i,j]=max(f[i-1,j],a[i].y+b[i]-j)其中b[i]为前i个人排队所用的总时间

然而200*40000好像有点大,降维呗!

类似背包一样降维就行

code by std:

#include<bits/stdc++.h>
using namespace std;
struct lsg{int x,y;}a[1000];
int n,f[400001],sum,ans,b[1000];
bool pd(lsg x,lsg y){return x.y>y.y;}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for (int i=1;i<=n;i++)cin>>a[i].x>>a[i].y;
    sort(a+1,a+1+n,pd);memset(f,10,sizeof(f));f[0]=0;
    for (int i=1;i<=n;i++)b[i]=a[i].x+b[i-1];
    for (int i=1;i<=n;i++){
            for (int j=sum;j>=0;j--){
                f[j+a[i].x]=min(f[j+a[i].x],max(f[j],a[i].y+j+a[i].x));//将i加入第一个队列
                    f[j]=max(f[j],a[i].y+b[i]-j);//将i加入第二个队列
                }
            sum+=a[i].x;
        }
    ans=1e9;
    for (int i=1;i<=sum;i++)ans=min(ans,f[i]);
    cout<<ans<<endl;
}

https://www.luogu.org/problem/P2467

这是一道好题

题目描述

求1-n排列组成的波动数列的个数

因为要比较大小关系所以dp里面最后数是多少是要记录的又因为是每个数都不重复的排列

所以定义dp[i,j]表示用前 i 个数最后一个数为 j 的方案数

dp[i,j]相当于dp[i-1,k]中原排列大于等于j的数都加1,再把j插到末尾后的新合法排列的方案数

答案有“M"型与"W"型,显然方案数是一样的,这里只考虑"W"型的,最后把答案*2就行了

用一个前缀和维护一下就好

这时你可能会有疑问，为什么偶数是枚举[1,j-1]，而奇数是枚举[j,i-1],

因为只考虑“W”形态的，所以奇数一定是山峰的，而偶数一定山谷；

偶数就不用再每个加一了直接加进去就好奇数就要每个大于等于 j 的加一

所以奇数枚举的一定要比前一个位置上的数大，偶数枚举的一定要比前一个位置上的数小

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 4211
#define M(a) ((a)<=mod?(a):(a-mod))
inline int read(){
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<3)+(x<<1)+c-'0';
        c=getchar();
    }
    return x*f;
}
int n,mod;
int dp[N][N],ans=0;
int b[N];
int lowbit(int x){
    return x&(-x);
}
void Add(int x,int d){
    while(x<=n){
        b[x]=M(b[x]+d);
        x+=lowbit(x);
    }
}
int Ask(int x){
    int ans=0;
    while(x){
        ans=M(ans+b[x]);
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    n=read(),mod=read();
    for(int i=1;i<=n;i++){
        dp[1][i]=1;
        Add(i,1);
    }
    for(int i=2;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i&1){
                if(i>j){
                    dp[i][j]=M(Ask(i-1)-Ask(j-1)+mod);
                }
            }
            else{
                dp[i][j]=Ask(j-1);
            }
        }
        memset(b,0,sizeof(b));
        for(int j=1;j<=n;j++){
            Add(j,dp[i][j]);
        }
    }
    for(int i=1;i<=n;i++){
        ans=M(ans+dp[n][i]);
    } 
    cout<<2*ans%mod<<endl;
    return 0;
}

https://www.luogu.org/problem/P1005

分析：

发现啊，每一行怎么取数是互不干扰的，则，只用分别处理每一行就好

数据范围也在算法复杂度以内

很好联想到区间dp

dp[i,j]表示处理到该行，区间[i,j]的最优解

考虑怎么转移

只有从[i-1,j]和[i,j+1]转移过来（因为转移逐渐将区间缩小）

因为题目中说要取完，但是空区间是DP不出来的，然后就得手动模拟每个长度为1的区间

具体高精啊，区间dp啊，见代码了

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>

using namespace std;

const int MAXN = 85, Mod = 10000; //高精四位压缩大法好 
int n, m;
int ar[MAXN];

struct HP {
    int p[505], len;
    HP() {
        memset(p, 0, sizeof p);
        len = 0;
    } //这是构造函数，用于直接创建一个高精度变量 
    void print() {
        printf("%d", p[len]);  
        for (int i = len - 1; i > 0; i--) {  
            if (p[i] == 0) {
                printf("0000"); 
                continue;
            }
            for (int k = 10; k * p[i] < Mod; k *= 10) 
                printf("0");
            printf("%d", p[i]);
        }
    } //四位压缩的输出 
} f[MAXN][MAXN], base[MAXN], ans;

HP operator + (const HP &a, const HP &b) {
    HP c; c.len = max(a.len, b.len); int x = 0;
    for (int i = 1; i <= c.len; i++) {
        c.p[i] = a.p[i] + b.p[i] + x;
        x = c.p[i] / Mod;
        c.p[i] %= Mod;
    }
    if (x > 0)
        c.p[++c.len] = x;
    return c;
} //高精+高精 

HP operator * (const HP &a, const int &b) {
    HP c; c.len = a.len; int x = 0;
    for (int i = 1; i <= c.len; i++) {
        c.p[i] = a.p[i] * b + x;
        x = c.p[i] / Mod;
        c.p[i] %= Mod;
    }
    while (x > 0)
        c.p[++c.len] = x % Mod, x /= Mod;
    return c;
} //高精*单精 

HP max(const HP &a, const HP &b) {
    if (a.len > b.len)
        return a;
    else if (a.len < b.len)
        return b;
    for (int i = a.len; i > 0; i--)
        if (a.p[i] > b.p[i])
            return a;
        else if (a.p[i] < b.p[i])
            return b;
    return a;
} //比较取最大值 

void BaseTwo() {
    base[0].p[1] = 1, base[0].len = 1;
    for (int i = 1; i <= m + 2; i++){
        base[i] = base[i - 1] * 2;
    }
} //预处理出2的幂 

int main(void) {
    scanf("%d%d", &n, &m);
    BaseTwo();
    while (n--) {
        memset(f, 0, sizeof f);
        for (int i = 1; i <= m; i++)
            scanf("%d", &ar[i]);
        for (int i = 1; i <= m; i++)
            for (int j = m; j >= i; j--) { //因为终值是小区间，DP自然就从大区间开始 
                f[i][j] = max(f[i][j], f[i - 1][j] + base[m - j + i - 1] * ar[i - 1]); 
                f[i][j] = max(f[i][j], f[i][j + 1] + base[m - j + i - 1] * ar[j + 1]);
            } //用结构体重载运算符写起来比较自然 
        HP Max;
        for (int i = 1; i <= m; i++)
            Max = max(Max, f[i][i] + base[m] * ar[i]);
        ans = ans + Max; //记录到总答案中 
    }
    ans.print(); //输出 
    return 0;
}

https://www.luogu.org/problem/P2511

分析

第一问，求最长的最短，很显然一个二分就行

那第二问计数

f[i,j]代表前i个数分成j块的方案数,

则f[i,j]=Σ f[k,j-1] (k>=left[i]&&k<i) ，而因为空间问题，是不可以开1000*50000个数组的，

考虑用到前缀和因为[ , j ] 都是由 [ , j-1]转移过来的直接降维每次更新完f数组最后更新前缀数组s

这是一道非常好的动规优化

时间复杂度（N*M）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;

int read()
{
    int x=0,f=1;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return x*f;
}

const int mod=10007;
const int maxn=50010;
int n,m,mx,ans;
int a[maxn],sum[maxn];
int dp[maxn],S[maxn];
int rem[maxn];

int check(int x)
{
    int tot=0,len=0;
    for(int i=1;i<=n;++i)
    {
        if(len+a[i]>x) tot++,len=a[i];
        else len+=a[i];
        if(tot>m) return 0;
    }
    return tot<=m;
}

int DP(int x)
{
    int k=0;
    for(int i=1;i<=n;++i)
    for(;k<i;++k)
    if(sum[i]-sum[k]<=x){ rem[i]=k; break;}
    
    int res=(sum[n]<=x);//因为后面是从2开始枚举的 特判是否有只能为1段的情况

    for(int i=1;i<=n;++i)
    {
    	if(sum[i]<=x) dp[i]=1;//初始化很重要 此时的dp[i] 表示前i个数分为1段的方案 如果没法分为1段的dp值就为0
    	S[i]=(S[i-1]+dp[i])%mod;
    }
    
    for(int i=2;i<=m+1;++i)
    {
        for(int j=1;j<=n;++j)
        {
            dp[j]=S[j-1];
            //非常常见的一种方法 用于转移的时候数组下标可能为负 取0
            if(rem[j]-1>=0) dp[j]=((dp[j]-S[rem[j]-1])%mod+mod)%mod;//注意减法出现负数
        }
        for(int j=1;j<=n;++j)
        S[j]=(S[j-1]+dp[j])%mod;
        
        res=(res+dp[n])%mod;
    }
    return res;
}

int main()
{
    n=read();m=read();
    for(int i=1;i<=n;++i) 
    a[i]=read(),sum[i]=sum[i-1]+a[i],mx=max(mx,a[i]);
    
    int L=mx,R=sum[n],mid;
    while(L<R)
    {
        mid=L+R>>1;
        if(check(mid)) ans=mid,R=mid;
        else L=mid+1;
    }
    printf("%d %d",ans,DP(ans));
    return 0;
}

标签：专题,int,max,HP,len,include,dp
来源： https://www.cnblogs.com/wzxbeliever/p/16525928.html