UVA1400 "Ray, Pass me the dishes!" 题解
作者:互联网
PART 1:题目大意
题目意思很明了:给定一个长度为 \(n\) 的序列 \(D\),求它的最大子段和
PART 2:解题思路
求最大子段和,我们考虑用线段树做。
用线段书如何维护最大子段和呢?我们看到如下一张图:
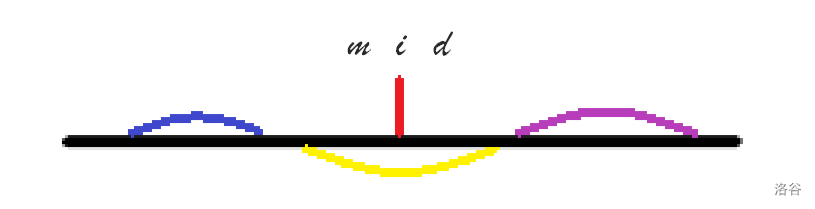
如图是一个区间,我们分别算得了其左子区间和右子区间的最大子段和(图中标记为蓝色和紫色)。我们的答案的子区间位置有三种可能:
1.全部位于左子区间内
2.全部位于右子区间内
3.一部分位于左子区间,另一部分位于右子区间
对于 1,2 两种情况,我们的答案分别就是其左子区间或右子区间的最大子段和。对于第三种情况,也就是图中的黄色部分。
那么黄色部分怎么求呢?仔细分析,为了使得黄色部分的值最大,那么它的值一定是左子区间的最大后缀和加上右子区间的最大前缀和。如果不是这样的话,那么值一定会更小。
所以我们可以在维护线段树的时候,除了像正常维护线段树的时候只需要维护左端点,右端点,题目要求答案三个值以外,还要维护当前区间的最大前缀和和最大后缀和,同时按照题目的要求,我们重新定义大于号和小于号:
typedef long long ll;
// 区间类型,便于计算
struct sec{
/*
l -> 区间左端点
r -> 区间右端点
sum -> 区间和
*/
int l,r;
ll sum;
sec operator + (const sec &b){
sec ans;
ans.sum = this->sum + b.sum;
ans.l = min(this->l,b.l);
ans.r = max(this->r,b.r);
return ans;
}
};
bool operator < (sec a,sec b){
if(a.sum == b.sum){
if(a.l == b.l) return a.r > b.r;
return a.l > b.l;
}
return a.sum < b.sum;
}
bool operator > (sec a,sec b){
if(a.sum == b.sum){
if(a.l == b.l) return a.r < b.r;
return a.l < b.l;
}
return a.sum > b.sum;
}
// 线段数节点类型
struct node{
/*
max_sec -> 最大子区间
max_pre -> 最大前缀子区间
max_lst -> 最大后缀子区间
sum_sec -> 区间和
*/
int l,r;
sec max_sec,max_pre,max_lst,sum_sec;
};
ll num[MAXN],sum[MAXN];
按照我们的定义,我们可以写出线段树中的上推,建树,查找函数,由于题目不要求修改,修改和下推的函数就不需要了:
// 寻找最大前缀和
sec find_max_pre(int now,int r){
if(tree[now].max_pre.r <= r) return tree[now].max_pre;
int mid = (tree[now].l + tree[now].r) >> 1;
if(r <= mid) return find_max_pre(lson,r);
else{
sec l_pre,r_pre;
l_pre = find_max_pre(lson,mid);
r_pre = find_max_pre(rson,r) + tree[lson].sum_sec;
return max(l_pre,r_pre);
}
}
// 寻找最大后缀和
sec find_max_lst(int now,int l){
if(tree[now].max_lst.l >= l) return tree[now].max_lst;
int mid = (tree[now].l + tree[now].r) >> 1;
if(l > mid) return find_max_lst(rson,l);
else{
sec l_lst,r_lst;
r_lst = find_max_lst(rson,mid);
l_lst = find_max_lst(lson,l) + tree[rson].sum_sec;
return max(r_lst,l_lst);
}
}
// 上推
void push_up(int now){
sec tmp = tree[lson].max_lst + tree[rson].max_pre;
// 处理最大子区间
tree[now].max_sec = max(tree[lson].max_sec,tree[rson].max_sec);
tree[now].max_sec = max(tree[now].max_sec,tmp);
// 处理最大前缀子区间
sec max_rpre = find_max_pre(rson,tree[now].r) + tree[lson].sum_sec;
tree[now].max_pre = max(tree[lson].max_pre,max_rpre);
// 处理最大后缀子区间
sec max_llst = find_max_lst(lson,tree[now].l) + tree[rson].sum_sec;
tree[now].max_lst = max(tree[rson].max_lst,max_llst);
// 处理区间和
tree[now].sum_sec = tree[lson].sum_sec + tree[rson].sum_sec;
}
// 建树
void build(int now,int l,int r){
tree[now].l = l; tree[now].r = r;
if(tree[now].l == tree[now].r){
tree[now].max_sec = tree[now].max_lst = tree[now].max_pre = tree[now].sum_sec = (sec){l,r,num[l]};
return ;
}
int mid = (l + r) >> 1;
build(lson,l,mid); build(rson,mid+1,r);
push_up(now);
}
// 查询
sec query(int now,int l,int r){
if(tree[now].l >= l && tree[now].r <= r){
return tree[now].max_sec;
}
int mid = (tree[now].l + tree[now].r) >> 1;
if(r <= mid) return query(lson,l,r);
else if(l > mid) return query(rson,l,r);
else{
sec res = max(query(lson,l,mid),query(rson,mid+1,r)); // 左子区间和右子区间的最大子段区取最大值
sec tmp = find_max_lst(lson,l) + find_max_pre(rson,r);// 横跨左子区间和右子区间的情况
return max(res,tmp);
}
}
注意细节的话,应该不难写对
PART 3:完整代码
其实前面都已经把主题部分贴出来了,这里再把完整代码放出来
#include<bits/stdc++.h>
#define MAXN 500010
#define lson now*2
#define rson now*2+1
using namespace std;
typedef long long ll;
struct sec{
int l,r;
ll sum;
sec operator + (const sec &b){
sec ans;
ans.sum = this->sum + b.sum;
ans.l = min(this->l,b.l);
ans.r = max(this->r,b.r);
return ans;
}
};
struct node{
/*
max_sec -> 最大子区间
max_pre -> 最大前缀子区间
max_lst -> 最大后缀子区间
sum_sec -> 区间和
*/
int l,r;
sec max_sec,max_pre,max_lst,sum_sec;
};
bool operator < (sec a,sec b){
if(a.sum == b.sum){
if(a.l == b.l) return a.r > b.r;
return a.l > b.l;
}
return a.sum < b.sum;
}
bool operator > (sec a,sec b){
if(a.sum == b.sum){
if(a.l == b.l) return a.r < b.r;
return a.l < b.l;
}
return a.sum > b.sum;
}
int n,m,cas;
ll num[MAXN],sum[MAXN];
node tree[MAXN<<2];
sec find_max_pre(int now,int r){
if(tree[now].max_pre.r <= r) return tree[now].max_pre;
int mid = (tree[now].l + tree[now].r) >> 1;
if(r <= mid) return find_max_pre(lson,r);
else{
sec l_pre,r_pre;
l_pre = find_max_pre(lson,mid);
r_pre = find_max_pre(rson,r) + tree[lson].sum_sec;
return max(l_pre,r_pre);
}
}
sec find_max_lst(int now,int l){
if(tree[now].max_lst.l >= l) return tree[now].max_lst;
int mid = (tree[now].l + tree[now].r) >> 1;
if(l > mid) return find_max_lst(rson,l);
else{
sec l_lst,r_lst;
r_lst = find_max_lst(rson,mid);
l_lst = find_max_lst(lson,l) + tree[rson].sum_sec;
return max(r_lst,l_lst);
}
}
void push_up(int now){
sec tmp = tree[lson].max_lst + tree[rson].max_pre;
// 处理最大子区间
tree[now].max_sec = max(tree[lson].max_sec,tree[rson].max_sec);
tree[now].max_sec = max(tree[now].max_sec,tmp);
// 处理最大前缀子区间
sec max_rpre = find_max_pre(rson,tree[now].r) + tree[lson].sum_sec;
tree[now].max_pre = max(tree[lson].max_pre,max_rpre);
// 处理最大后缀子区间
sec max_llst = find_max_lst(lson,tree[now].l) + tree[rson].sum_sec;
tree[now].max_lst = max(tree[rson].max_lst,max_llst);
// 处理区间和
tree[now].sum_sec = tree[lson].sum_sec + tree[rson].sum_sec;
}
void build(int now,int l,int r){
tree[now].l = l; tree[now].r = r;
if(tree[now].l == tree[now].r){
tree[now].max_sec = tree[now].max_lst = tree[now].max_pre = tree[now].sum_sec = (sec){l,r,num[l]};
return ;
}
int mid = (l + r) >> 1;
build(lson,l,mid); build(rson,mid+1,r);
push_up(now);
}
sec query(int now,int l,int r){
if(tree[now].l >= l && tree[now].r <= r){
return tree[now].max_sec;
}
int mid = (tree[now].l + tree[now].r) >> 1;
if(r <= mid) return query(lson,l,r);
else if(l > mid) return query(rson,l,r);
else{
sec res = max(query(lson,l,mid),query(rson,mid+1,r));
sec tmp = find_max_lst(lson,l) + find_max_pre(rson,r);
return max(res,tmp);
}
}
int main(){
while(~scanf("%d%d",&n,&m)){
for(int i = 1;i <= n;i++) scanf("%lld",&num[i]);
build(1,1,n);
cas++; printf("Case %d:\n",cas);
for(int i = 1;i <= m;i++){
int l,r;
scanf("%d%d",&l,&r);
sec ans = query(1,l,r);
printf("%d %d\n",ans.l,ans.r);
}
}
return 0;
}
标签:me,dishes,题解,sum,tree,lst,sec,max,now 来源: https://www.cnblogs.com/Elfin-Xiao/p/16508035.html