1. Arxiv 2021: Towards a Theoretical Framework of Out-of-Distribution Generalization

2. ICML 2021 Oral： Can Subnetwork Structure be the Key to Out-of-Distribution Generalization?

3. ICML 2021 Oral：Domain Generalization using Causal Matching

4. ICML 2021 Spotlight: Environment Inference for Invariant Learning

5. ICLR 2021 Poster: Understanding the failure modes of out-of-distribution generalization

6. CVPR 2021 Oral: Reducing Domain Gap by Reducing Style Bias

不断更新ing

Towards a Theoretical Framework of Out-of-Distribution Generalization

这篇文章应该是今年投稿NeurIPS的文章，文章贡献有2

1. 在OOD泛化受到极大关注的今天，一个合适的理论框架是非常难得的，就像DA的泛化误差一样。

2. 本文通过泛化误差提出了模型选择策略，不单纯使用验证集的精度，二是同时考虑验证集的精度和在各个domain验证精度的方差。

Preliminary

先来看一看OOD经典的问题建模，考虑一个多分类问题\(\mathcal{X}\rightarrow\mathcal{Y}=\{1,...,K\}\)。用\(\mathcal{E}_{avail}\subset\mathcal{E}_{all}\)表示可见的训练集，以及所有集合。\((X^e,Y^e)\)表示输入-标签组，OOD泛化问题就是要找一个分类器\(f^*\)来最小化worst-domain loss

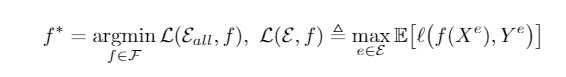
这里的\(\mathcal{F}:\mathcal{X}\rightarrow\mathbb{R}^K\)是假设空间，\(l(\cdot,\cdot)\)是损失函数。\(f\)同样可以分解为 \(g\circ h\)，即分类器和特征提取器。\(h:\mathcal{X}\rightarrow\mathbb{R}^d\)可以写为

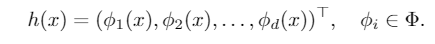
\(\phi\)是一个标量的特征映射，\(d\)是预设的特征维度。下文将\(\phi(X^e)\)简写为\(\phi^e\)。

Framework of OOD Generalization Problem

对OOD问题的分析难点在于如何构建\(\mathcal{E}_{avail}\)和\(\mathcal{E}_{all}\)之间的联系，以及域泛化和二者联系之间的联系。接下来我们就一步步的看看这篇文章是如何进行构建的

作者先介绍了两个定义：特征的“variation（变化）”和“informativeness（信息量）”。前者是一个类似于divergence的概念，我们希望对同一个label，在各个域上的特征变化不大。后者表示了这个特征要有足够的表示能力，包含了区分各个标签的能力。

1. Variation: 给定如下定义，如果一个特征满足\(\mathcal{V}(\phi,\mathcal{E})\leq\varepsilon\)，那么我们说他是是\(\varepsilon\)-invariant的，

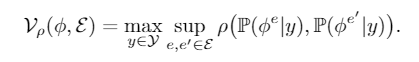
1. Informativeness： 给定如下定义，如果一个特征满足\(\mathcal{I}(\phi,\mathcal{E})\leq\delta\)，那么我们说他是是\(\delta\)-Informative的，

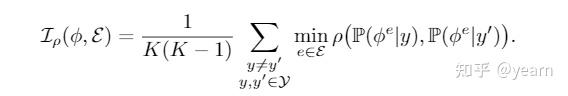
有了这两个定义，接下来就进入最难的环节，构建\(\mathcal{E}_{avail}\)和\(\mathcal{E}_{all}\)之间的联系，本文是基于这样一个假设“如果一个特征包含足够的信息，而且在\(\mathcal{E}_{avail}\)上能够做到invariant，那么就能够泛化到\(\mathcal{E}_{all}\)”，这个假设还是挺强的，但是暂时也没有更好的替代方案，从该假设来看，\(V(\phi,\mathcal{E}_{avail})\)，\(V(\phi,\mathcal{E}_{all})\)的联系捕获了OOD泛化的可行性和难度。为了定量的测量这个联系，我们还需要这样一个函数类

1. Expansion Function：这是一个函数\(s:\mathbb{R}^+\cup\{0\}\rightarrow\mathbb{R}^+\cup\{0,\infty\}\)，如果它满足 (i)单调递增且\(s(x)\geq x\) (ii)\(\lim_{x\rightarrow 0} s(x)=s(0)=0\)，我们称之为一个扩增函数。

这个函数定义了\(V(\phi,\mathcal{E}_{avail})\)，\(V(\phi,\mathcal{E}_{all})\)之间的关系，我们可以想一下，如果可见域只是全部域的一小部分，那么\(s\)就是一个非常陡峭的函数，否则如果可见域就是全体域，那么\(s(x)=x\)。

有了这三样东西，我们来定义最后一个最重要的概念

1. Learnability： 对所有满足信息容量\(I_\rho(\phi,\mathcal{E}_{avail})\geq \delta\)的特征提取器而言，如果存在上述的\(\delta\)和一个扩增函数\(s(\cdot)\)，使得\(s(V(\phi,\mathcal{E}_{avail}))\geq V(\phi,\mathcal{E}_{all})\)我们称一个OOD问题是可学习的。

原文还提供了一些讨论帮助读者更好的理解这几个问题。

Generalization Bound

接下来的推导就是文章最复杂的部分了，对于分类器\(f=g\circ h\)，我们定义泛化误差为

\(err(f)=\mathcal{L}(\mathcal{E}_{all}, f)-\mathcal{L}(\mathcal{E}_{avail}, f) \\\)

这里只有一个假设：损失函数有界 \(l(\cdot,\cdot)\in[0,C]\)。接下来主要讲讲对它证明的直观理解，不涉及具体推导。

首先上述损失可以推导出这样一个bound，这一步将loss之间的差值转化为了\((h|y)\)分布之差

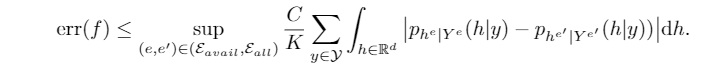
接下来就要根据假设，将分布的差转化为常数项和Variation或者Informativeness相关的项，这里用到了傅里叶反变换公式以及较多的数学转化，最终得到了如下这样一个复杂的结果，

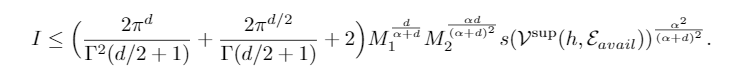
将常数项简化一下就得到了误差上界

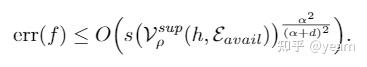
类似的，我们也可以推出一个下界

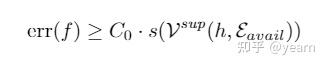
看到这里可能有人疑惑了，上下界都和variation有关，但是和Informativeness无关，那我输出全0向量不就可以做到invariant了吗？答案是否定的，在bound的证明中总是假设该问题满足Learnability，而Learnability关键的一点就是限制信息容量大于一个定值。所以这个bound对我们的启发在于，为了追求良好的OOD性能，OOD算法应同时注重提高预测性能和控制variation的变化（好像大家一直都是这么做的）。

Variation as a Factor of Model Selection Criterion

本文中提出了一种新的模型选择策略，如果我们按照验证集的总体精确度来选择最终的模型，其实没有几个模型比ERM好很多，这一结果并不奇怪，因为传统的选择方法主要关注(验证)准确性，这在OOD概化中有偏倚。相反本文没有单独考虑验证精度，而是将其与variation相结合，选择了高验证精度和低variation的模型。文中也通过实验验证了这种选择策略的有效性。其中"val"就是传统的模型选择策略。

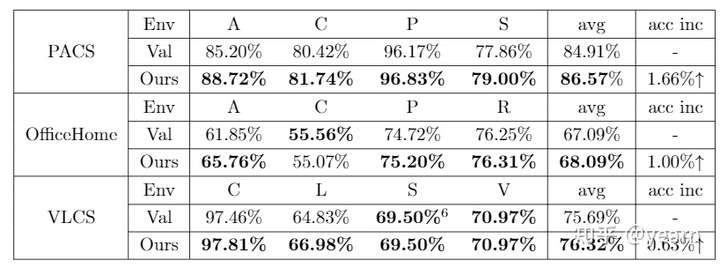
Can Subnetwork Structure be the Key to Out-of-Distribution Generalization?

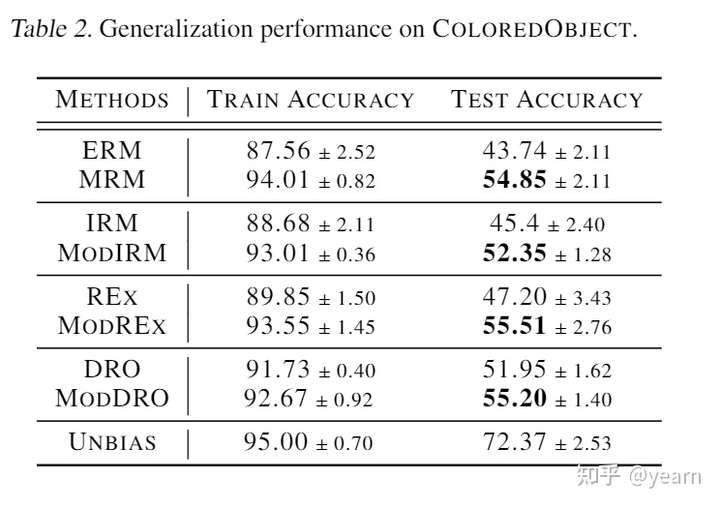
本文基于彩票假设，即使我们整体的模型是有偏的（偏向背景，上下文而不是物体本身），这个网络中也存在一些子网络他们是无偏的，可以实现更好的OOD性能。文中提供了模块风险最小化MRM来寻找这些“彩票”。

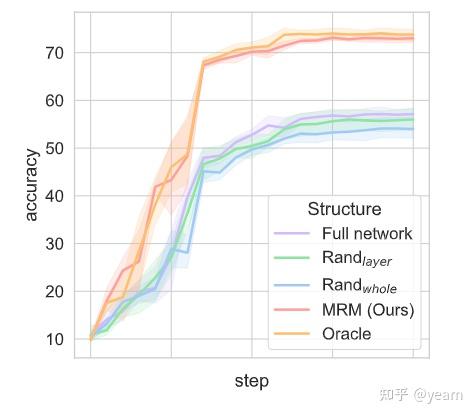
MRM算法理解起来也并不困难

1. 给定数据，完整的网络，子网络的logits \(\pi\) ，logit是一个用于产生mask的随机分布，比如网络第\(l\)层有\(n_l\)个参数，那么\(\pi_l\in\mathbb{R}^{n_l}\)。该层的mask通过从\(sigmod(\pi_l)\)中采样得到，mask \(m\)将完整网络转化为子网络（\(m_{l,i}\)=0即忽略第\(l\)层的第\(i\)个参数）

2. 我们对模型进行初始化然后使用ERM的目标进行训练\(N_1\)个step。wz

3. 我们从整个网络中采样子网络，结合交叉熵和稀疏正则化作为损失函数来学习有效的子网结构。

4. 最后只需要简单地只使用所得到的子网中的权值重新进行训练，并将其他权值固定为零。

文章最大的亮点就在于MRM和目前主流的研究方向（修改目标函数）是正交的，无论目标函数是什么，MRM都能找到这么些泛化能力更强的子网络。

Domain Generalization using Causal Matching

这篇文章乍一看非常简单，但是细看之后发现其实有很多地方理解起来并不容易。

这篇文章的主要贡献在于

1. 作者argue了一件事情，我们以往学习的不变性特征表达包括 \(P(\Phi(x^{(d)})|Y)\) 与domain无关还是 \(P(\Phi(x))\) 与domain无关其实都是有问题的，根据文中假设的因果图来看，要真正捕捉到域不变特征，我们需要约束 \(P(Y|X_C)\) 不变，其中 \(X_C\) 是图像的object信息。

2. 作者加了一项看着很简单的约束：拥有相同的对象（object）的跨域图像也应该有相同的表示。

文中涉及的证明比较多，这里只阐述high-level的观点。首先我们来分析一下传统的ERM算法

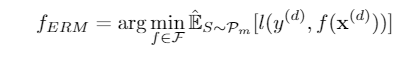
\(P_m,P\) 分别是我们可见的数据分布和总体的数据分布，文中证明了当可见域的数目等于所有域，样本数量趋于正无穷时，ERM能够收敛到最优分类器。然而正常情况下我们的可见域只是数据域的一部分 \(D_m\subset D\) ，因此ERM就会过拟合。

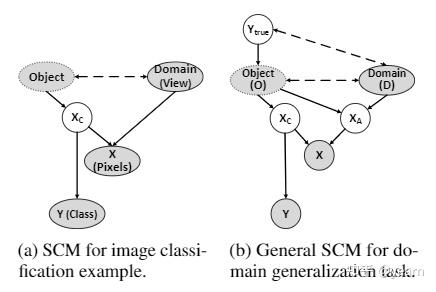
这是文中提出的结构化因果图，对因果不了解的朋友们无需担心，总之一大堆证明就是为了提出我们需要的object特征 \(X_C\) 要满足 \(X_C\bot D|O\) ，这个条件其实不难理解，就是说对同一个对象而言，它的特征不应该随着domain变化，所以文中在ERM的基础上添加了如下约束

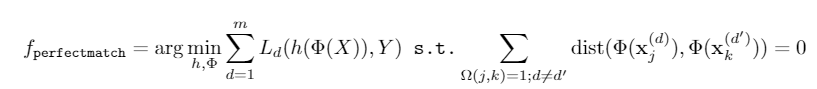
作者证明了

1. 满足上述约束的分类器中包含了最有分类器

2. 在具有虚假相关性的数据集中，优化如下的损失函数能够带来最优分类器。

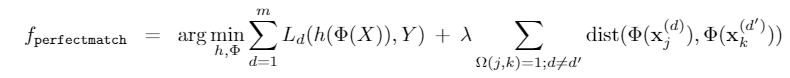
到这里文章的内容好像已经完整了？其实不然，考虑一个数据非常不平衡的数据集，一个domain中拥有超多object \(A\) ，其他domain基本没有，那么上述的match其实是在不断地减小同一个domain下同一类的特征距离，这对泛化是没有太大好处的。对于Rotated MNIST这类的数据集，因为是通过数据增强的方式构造的，因此非常的balance，但是对于更加真实的数据集，这个关系显然是不成立的，这就是我对于文中object information is not always available, and in many datasets there maynot be a perfect “counterfactual” match based on same object across domain这句话的理解。那么如何避免我们对class-balance的过度依赖，在没有非常好的counterfactual sample的情况下也能近似上述的约束呢？答案是学习一个matching，这才是文章的关键。

因此接下来文章的逻辑就比较清晰了，作者将算法分成了两部分，首先学习一个match，然后再利用这个match近似上面的约束

具体的实现过程是这样的

Initialization（构造random match）：首先我们对每一个类选择一个基域（包含该类元素最多的类），对基类的所有数据点进行遍历。对每个数据点，我们随机的在剩下 \(K-1\) 个域中给他匹配标签相同的元素，因此会构造出一个 \((N',K)\) 大小的数据矩阵，这里 \(N'\) 即所有类的基域大小之和，K是总共的域的数目。

Phase 1: 采样一个batch的数据 \((B,K)\) ，对batch中的每个数据点最小化对比损失，和他具有相同object不同域的样本作为正样本，不同object样本作为负样本。

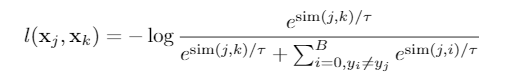
每 \(t\) 个epoch使用通过对比学习学到的representation更新一次我们的match。首先还是要选基域，但是在基域选定后，我们不再随机的在剩下域中挑选sample，我们为基域中的该类的每个样本在其他域中找representation距离最近的点作为正样本。

在Phase 1结束时，我们根据学习到的最终表示的 \(L_2\) 距离更新匹配的数据矩阵。我们称这些匹配为推论匹配。

Phase 2： 我们使用下列损失函数，但是match使用我们第一阶段学到的。网络从头开始训练（第一阶段学到的网络只是用来做匹配而已）。但是第一阶段学到的匹配可能不能包含所有的数据点，因此作者在每次训练除了从数据矩阵采样 \((B,K)\) 的数据外，还通过随机匹配再产生 \((B,K)\) 的数据。

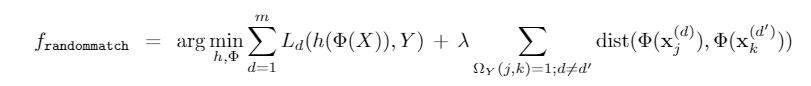
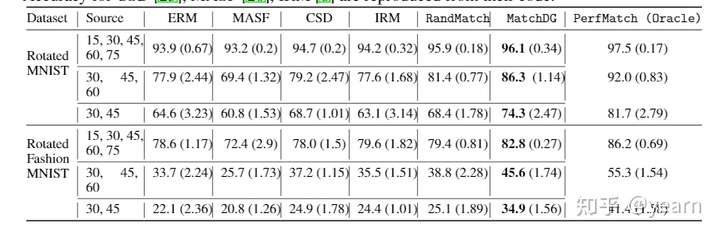
简单看一下实验效果，对MNIST类的任务，存在perfect match，效果非常显著。

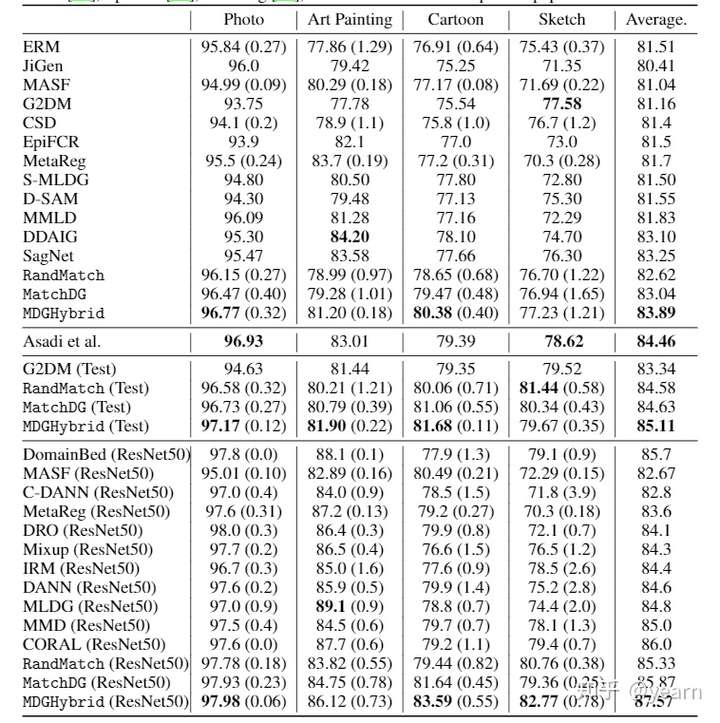
对PACS这类任务不存在perfect match，作者将MatchDG结合数据增强进一步提升（MDGHybrid），效果也是挺不错的。

Environment Inference for Invariant Learning

没有domain label怎么做OOD泛化？这篇文章就回答了这样一个有趣的问题。给出的答案也非常的interesting：我们自己推断domain label甚至能达到比使用真实域标签更好的性能。

首先文章的motivation在于，无论是从隐私还是标签的获取来看，域标签都是难以取得的。除此之外，在某些情况下，相关的信息或元数据(例如，人的注释、用于拍摄医疗图像的设备ID、医院或部门ID等)可能非常丰富，但目前还不清楚如何最好地基于这些信息指定环境。设计算法避免人工定义环境是这篇文章的出发点。

所以很直观的，算法应该分成两部走

1. 推断环境标签

2. 利用环境标签学习域不变性特征。

文章的模型很有意思，我们先选择一个已有的学习域不变特征的算法（模型 \(\tilde{\Phi}\) ）,文中用了IRM和GroupDRO

1. 在第一步推断标签的时候，我们选择最违背域不变特征的标签分配方式，分配标签使得IRM，GroupDRO这些算法的分类性能最差。即固定住模型 \(\Phi\leftarrow\tilde{\Phi}\) ，然后优化EI （environment inference EI）目标，估计标签变量 \(\mathbf{q}^*=\arg\max_{\mathbf{q}} C^{EI}(\tilde{\Phi},q)\) 最违背域不变特征。

2. 固定住我们inference的标签 \(\tilde{\mathbf{q}}\leftarrow\mathbf{q}^*\) ，优化invariant learning (IL)目标来产生新模型 \(\mathbf{\Phi}^*=\arg\min_{\mathbf{q}} C^{IL}({\Phi},\tilde{q})\)

那么现在未知量就剩下了EI, IL这两个目标如何构造。IL其实就是IRM，GroupDRO的优化目标本身。对于IRM来说既是

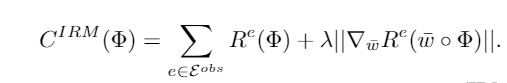
那么对于EI目标，差别只是在于EI的时候没有现成的enviroment label可以用，也就是说传统IRM的逐环境损失可以写作如下形式

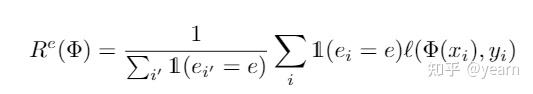
其中 \(1(e_i=e')\) 是环境自带的domain label，这时候我们没有这个东西，因此将其替换为我们的概率分布 \(q_i(e'):=q(e'|x_i,y_i)\) ，一个soft版本的domain label。我们只需要优化这个概率分布，使得本轮固定的分类器 \(\Phi\) 更差即可。

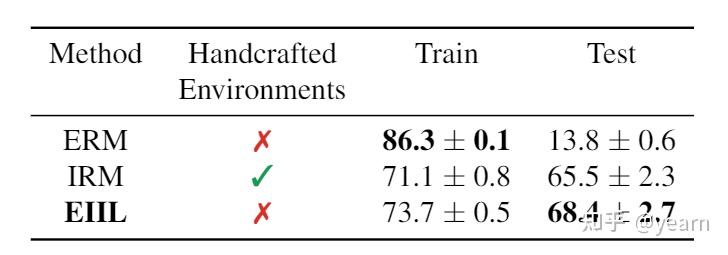
有趣的是，即使domain label是可用的，他也不比我们推断出来的label好。EIIL使用推断出来的label，比直接使用IRM好更多。

Understanding the failure modes of out-of-distribution generalization

Motivation

现有的理论可以解释为什么当不变性特征本身信息不足时，分类器依赖于虚假特征(下图a)。但是，当不变特征完全能够预测标签时，这些解释就不成立了。比如在下图b中，显然我们只需要max-margin就可以很好的识别camel和cow，但是真实情况是，分类器依然会依赖于这些虚假特征，其实在很多现实设置中，形状或者说轮廓信息是完全可以预测对应的标签的，但是我们的分类器总会依赖于类似于背景或者颜色等虚假的信息。作者发现了两个影响因素，这是本文的核心贡献。

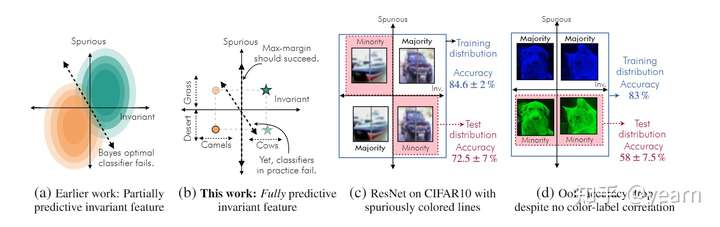
Easy to learn domain generalization tasks

之前的探索ERM失败原因的工作主要基于两种模式

1. 不变性特征和虚假特征都只能部分预测标签，因此一个优化负对数似然的分类器当然不能错过虚假特征包含的信息。

2. 不变性特征和虚假特征都能完全预测标签，但是虚假特征更容易学习（更加线性），因此梯度下降会选择更容易学习的特征进行分类。

本文对这些假设进行了质疑，构造任务时针对以上每一点进行了回应，其任务有以下特点

1. 不变性的特征有足够的能力完成对标签的预测，虚假特征不能完全预测标签。

2. 不变性特征有一个线性的分类boundary，很好学习。

作者验证了，即使在这样一个易学习的任务中，ERM仍然还是依赖于虚假特征。作者总结并验证了两个原因

Failure due to geometric skews.

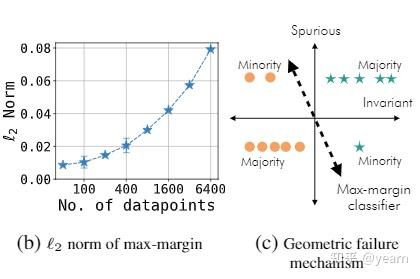
首先文中指出了一点，随着数据量的增大，max-margin分类器的\(l_2\) norm也随之增大，geometric skews是一个非正式的称谓，用于形容过参数化的神经网络，考虑上图c中的场景，我们可以把数据集分为两类：

1. 多数类 \(S_{maj}\)，对应cow/camel在green/yellow背景下。

2. 少数类 \(S_{min}\)，对应cow/camel在yellow/green背景下。

假设我们使用不变性特征来进行预测将花费 \(||w_{all}||\)的 \(l_2\) norm，使用不变性特征对少数类进行预测的花费为 \(||w_{min}||\)，因为数据量的原因，\(||w_{min}< w_{all}||\)。

那么此时我们还可以这样进行预测： 使用虚假特征作为捷径来预测多数类，然后使用不变性特征来预测少数类，这种方式需要更少的\(l_2\) norm，因此更容易成为我们max-margin分类器选择的策略。

Failure due to statistical skews

上文研究的是max-margin分类器，我们知道对于一个线性分类器而言，在一定条件下，在线性可分离的数据集上，这些分类器会在无限时间下收敛到max-margin分类器，也就是说即使他收敛了也会收到geometric skew的影响。那么这个收敛过程本身会不会引入一定的spurious correlation呢。

作者通过观察发现，即使我们的数据集不存在geometric skew，即max-margin分类器不会失败，我们花费超长时间训练一个线性分类器使他收敛，他依然会依赖于虚假特征。作者在文章推导出了一个收敛性随伪相关而变化的bound来讨论使用梯度下降训练的过程中引入的伪相关，

总结一下，目前大部分注意力都集中在实用主义或启发式解决方案(设计或学习“不变”特性的各种技巧)上，而我们对OOD情况中出错原因的基本理解仍然不完整。本文旨在通过研究简化的设置来填补这些理解上的空白，并提出这样一个问题:当任务可以只使用安全的(“不变的”)特性来解决时，为什么统计模型要学习使用易变化的特性(“虚假的”特性)。在制定了多个约束条件(保证对容易学习的任务适用)后，他们表明失败有两种形式:几何倾斜和统计倾斜。他们依次进行分析和解释，同时也提供了说明性的实证结果。

Reducing Domain Gap by Reducing Style Bias

CNN对图像纹理这类的风格元素具有很强的归纳偏置，因此对域变化非常敏感。相反其对物体形状这类真正和标签相关的元素却不敏感。本文提出了一种将style和content分离开的简单方法，可以作为一种新的backbone。

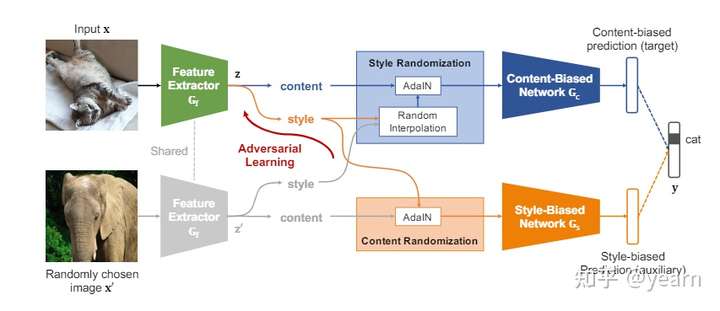
文章结构非常简单，一个feature extractor两个head。content-bias head想要做的事是将style信息打乱，同时还确保分类结果正确，也就是让这个head更关注于content信息。相反style-bias head将风格信息打乱，让这个head更关注于style信息，与此同时一个对抗学习就可以让backbone产生更少的style-bias representation。

看到这里其实难点已经很明确了，**如何将style/content信息打乱? **文章基于这样一个假设，channel-wise的均值和方差作为风格信息，spatial configuration作为style信息，这样一个假设已经被以往很多工作采用了，不过本文提出了一个更新的使用方式。首先我们来看如何打乱style信息

先求一个channel-wise的均值和方差

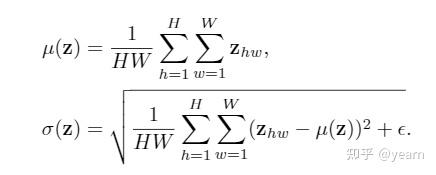
然后文中提出了一个SR模块，通过将 \(z\) 和另一个随机的 \(\bar{z}\) 的风格信息进行插值，构造一个随机的 \(\tilde{\mu},\tilde{\sigma}\) ，然后通过AdaIN将 \(z\) 的风格信息替换成这个随机的风格，这样就完成了风格的shuffle

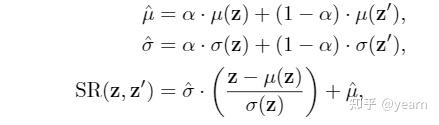
接下来我们只需要将这个通过SR模块的representation喂给内容分类器 \(G_c\) 进行分类正常计算分类损失即可。

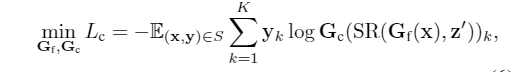
对于style-bias head，我们反其道而行之，构造一个CR模块

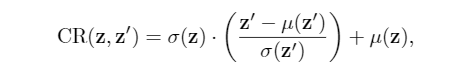
同样通过CR模块的representation喂给风格分类器，然后风格分类器的优化就是利用style信息来预测标签

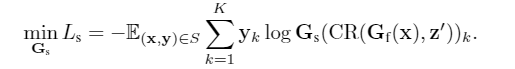
很直观的，我们可以想到，插入一个GRL来训练backbone，使得backbone产生更少的style信息，文中采取了类似的策略，只不过不是插入GRL，而是用了最大熵

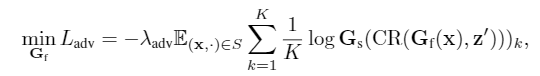
最大熵其实是具有很不错的性质的，在我最近的一篇工作中我简单的分析了这个类型的损失函数，他能起到风格信息和representation互信息最小化的作用。

Learning Domain Invariant Representations for Generalizable Person Re-Identification​arxiv.org/abs/2103.15890

具体如下面的式子， \(\mathcal{I}\) 即互信息， \(\mathcal{H}\) 即熵。

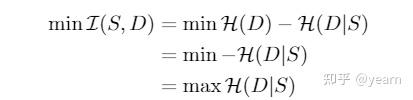
简单看一下在domain generalization上的实验结果

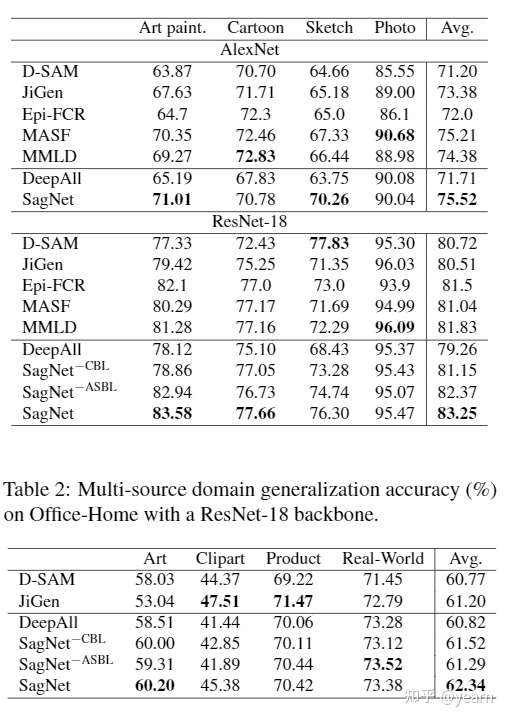
文章选择的baseline其实并不多，也没有resnet50这种大型backbone的结果，但是从文中展示的内容来看，SagNet相比于现有的大多数方法还是有一定优势的。对我而言我觉得难得的是，它提供了一种style/content信息新的提取方式，以往的工作往往需要两个encoder来提取content/style信息。

最后，新开了github整合自己OOD方面的阅读笔记，欢迎关注。

yfzhang114/Generalization-OOD-Reading-List​github.com/yfzhang114/Generalization-OOD-Reading-List
转
转

标签：OOD,domain,泛化,特征,标签,分类器,2021,mathcal
来源： https://www.cnblogs.com/-402/p/16504145.html