首页 > 其他分享> > 隐私计算技术：隐私求交（PSI）及其应用场景

隐私计算技术：隐私求交（PSI）及其应用场景

2022-07-21 15:37:02 作者：互联网

作者：珊竹

加入隐私计算交流群，和作者一起学习：SecretFlow01

01、The Problem of Private Set Intersection

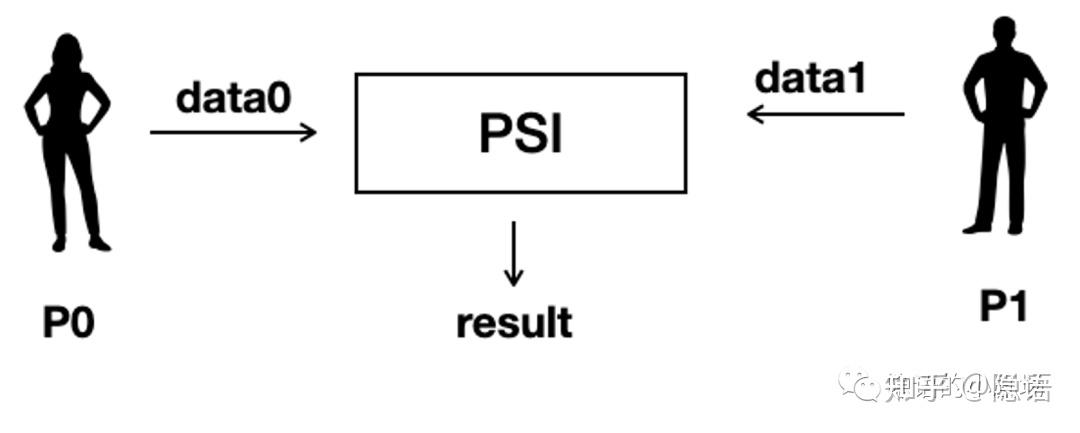
PSI 全称为 Private Set Intersection，直观的翻译名字为“隐私求交”。从场景来看，隐私求交：

有许多个参与方，每个参与方持有各自的隐私数据
希望通过协议求到所有数据的交集
但是不泄漏除交集外的任何信息

目前常用的 PSI 算法有：

ECDH [1]
KKRT [2]
PSTY [3]

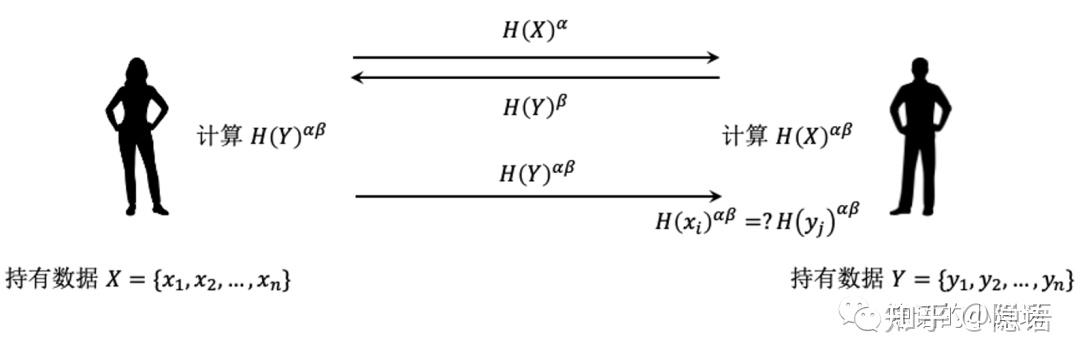
1.1. ECDH

如果我们假设哈希函数是计算安全参数，通常我们可以取 128，基于 DH 的 PSI 协议如下所示。

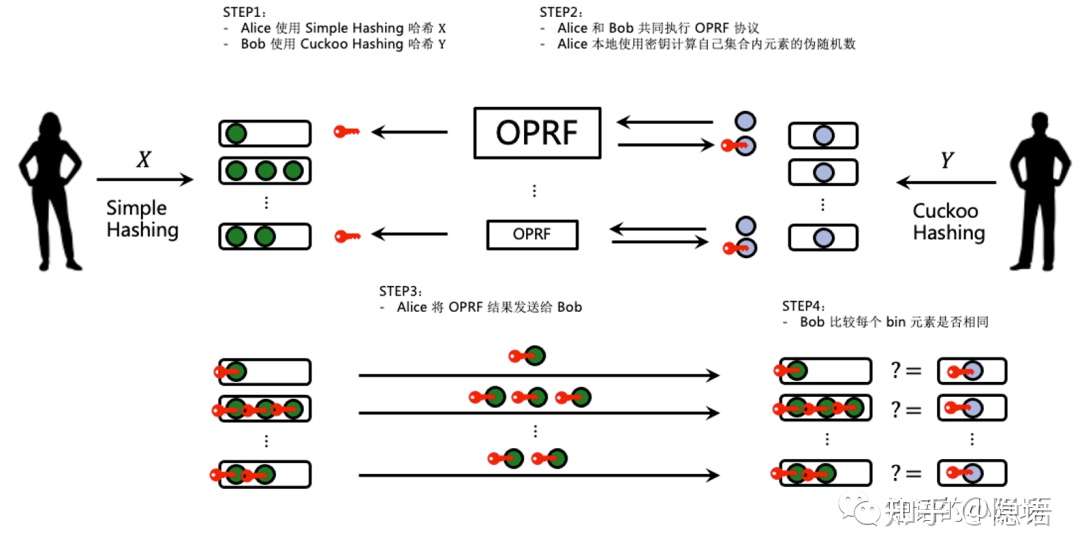
1.2. KKRT

结合 Cuckoo hash 以及 batched OPRF，可以构造出一个比较高效的基于 OT 的 PSI 协议（由于 batched OPRF 的构建基于 OT，因此我们可以认为 KKRT16 的 PSI 协议是基于 OT 构建的）。协议具体内容如下图所示，我们将左边参与方叫做 Alice，右边参与方叫做 Bob。

02、PSI 的应用场景

我们可以看到，（如果我们只考虑两方的场景下）PSI 场景中参与方我们记为 P0 以及 P1

P0 持有数据：data0 = (X, A1, A2, A3, ....)
P1 持有：data1 = (Y, B1, B2, B3, ....)

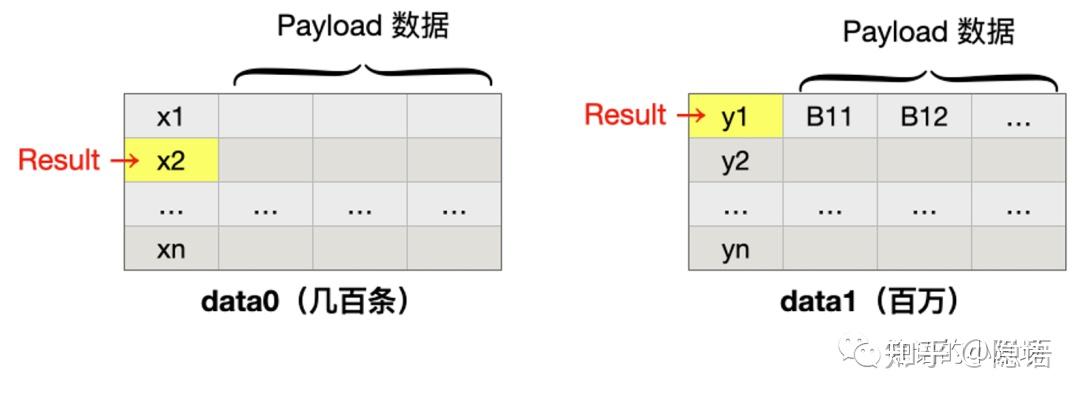
这里 X、Y 表示想要“撞库”使用的匹配字段（类似于 UID），而 Ai、Bi 指的是可能存在的其他数据信息。我们假设在所有两方 PSI 场景下想要比对的数据用下图方式表示。我们假设 data0 和 data 1 中只有一条数据是匹配的，即 y1 和 x2。

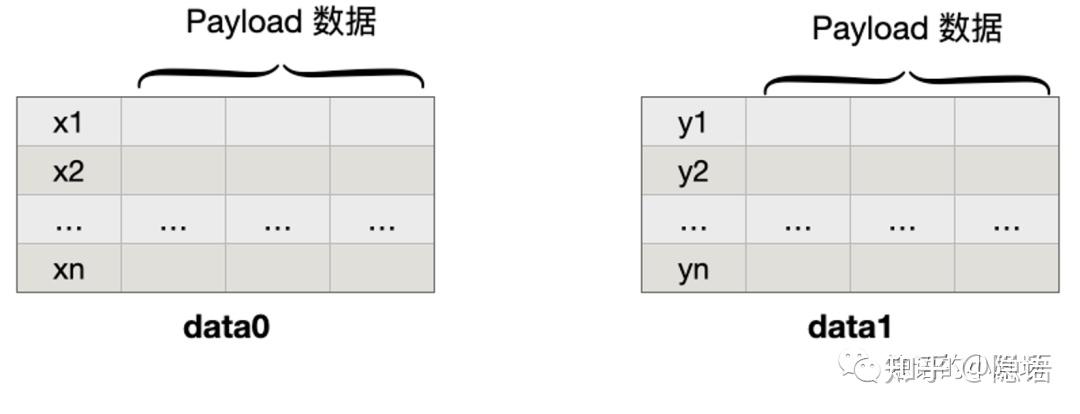
注意在 PSI 中我们一定需要保证安全的是：

X 与 Y 的非交集元素

Case 1: 指定参与方获取交集 UID

通常来说，在 PSI 中我们指定可以指定某个参与方（例如 P0）获取到 UID 的 PSI 结果。在下面这种场景下，

P0 得知了交集的 UID
P1 什么都没有得到

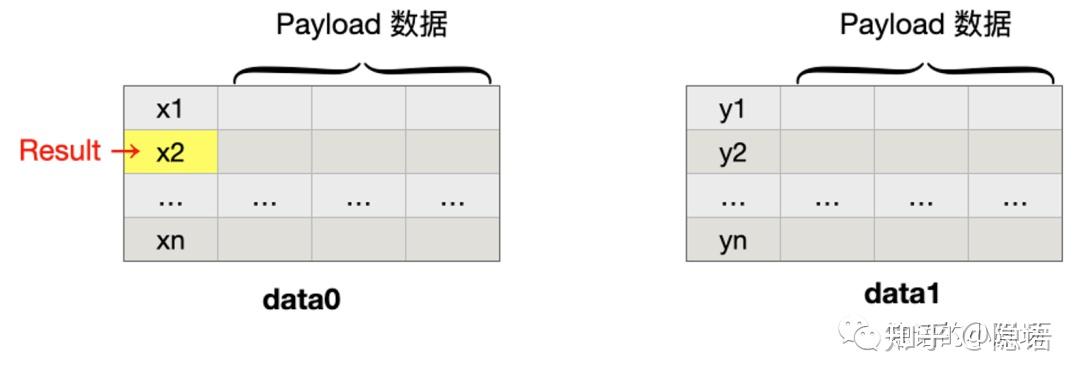
（几乎）所有的已知 PSI 协议都可以实现上述功能。例如 KKRT、ECDH PSI 等等。

Case 2: 指定参与方获取交集 UID 以及 Payload

通常来说，在 PSI 中我们指定可以指定某个参与方（例如 P0）获取到 UID 以及 Payload 的 PSI 结果。在下面这种场景下，

P0 得知了交集的 UID + 交集元素在 P1 处的 Payload
P1 什么都没有得到

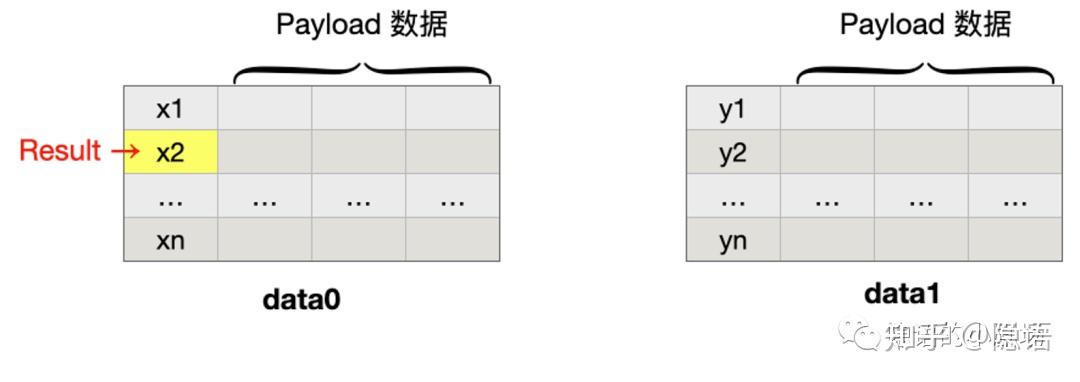
这种情况我们需要一些 tricky 的方式来计算，

通过 case1 首先使 P0 获取到 “x2” 这条交集的 UID 数据；
运行一个 Symmetric PIR 协议，或者 1-out-of-n OT 协议获取到 payload 的交集信息。

当然，也有一些更加高效的算法，这里不再赘述。

Case 3: 交集 UID 公开

在这个 case 中，双方均获取到最终交集的 UID 信息。

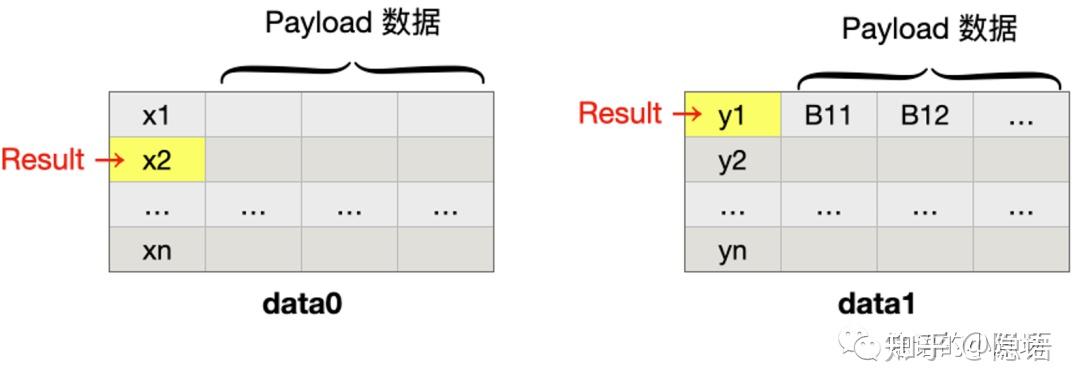
所有的已知 PSI 协议都可以实现上述功能。

Case 4: 交集 UID 公开，指定方获取到 Payload

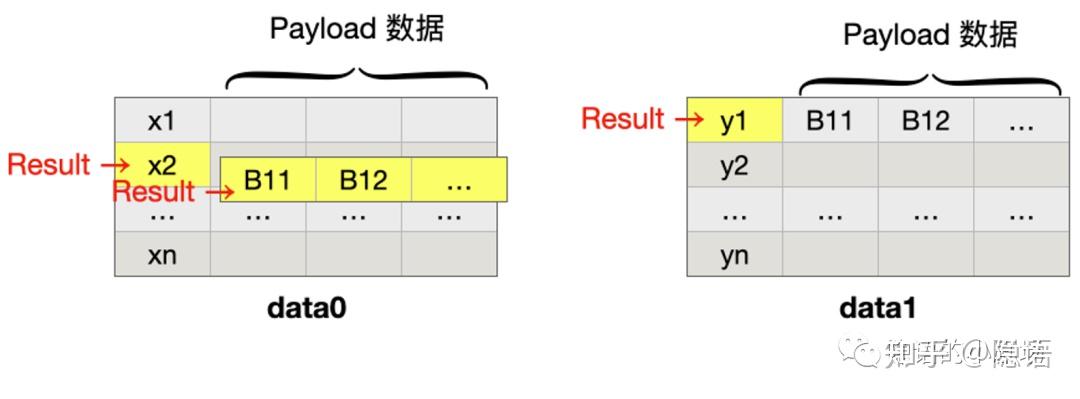
所有的已知 PSI 协议都可以实现上述功能。只需要在 case3 的基础上让 P1 将 payload 发送给 P0 即可。

Case 5: 双方数量级差距大（性能提升）

传统的 PSI 协议一般假设了双方数据集大小类似的情况，因此在 unbalanced 场景中我们需要特定设计的 PSI 协议来完成协议加速。需要注意的是在 unbalanced 的场景下其实并不影响我们解决 case 1 - case 4 的所有应用场景，这里我们只以 case 3 的场景作为例子。

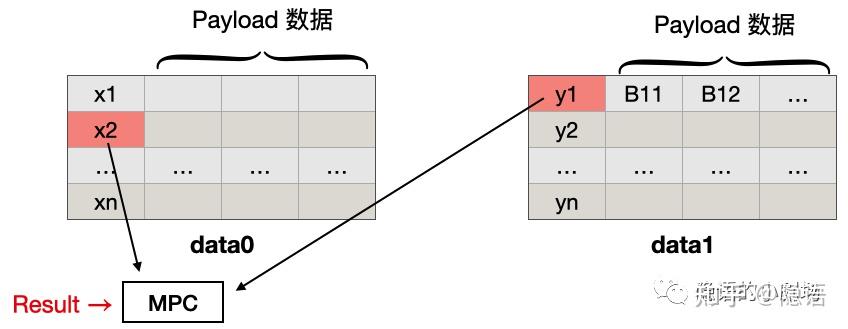
Case 6: 获取到交集 UID 或者 Payload 的统计值

在法律法规、用户隐私要求较高的场景中，我们需要对交集信息进行保护。因此在下面这种场景下，

P0 得知了双方交集 UID 的某个统计值
P1 得知了双方交集 UID 的某个统计值

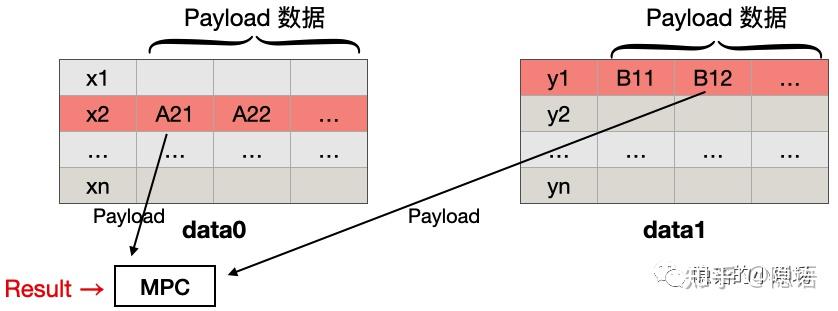
如果我们想要同时对 Payload 进行计算，会牺牲较大的性能，可以达到的效果是：

P0 得知了双方交集 UID 的某个统计值或者 Payload 的某个统计值
P1 得知了双方交集 UID 的某个统计值或者 Payload 的某个统计值

注：本文讨论的方案仅限于半诚实安全模型，恶意安全需要另行讨论。