首页 > 其他分享> > 【模板】扫描线面积并

【模板】扫描线面积并

2022-07-20 08:34:35 作者：互联网

例题：P5490 【模板】扫描线

update at 2022.5.28 更新到了当前版本(雾)的码风

因为切不动线段树合并就去搞扫描线了

虽然扫描线也搞了一晚上加半个上午

切入正题

扫描线是一种为了处理如多个矩形有重叠的覆盖在一起的不规则图形的算法。

如图：(图片来自网络)

整个图形的面积就转化成了\(∑\)各个矩形的面积。
需要做的就是用线段树维护这样一条扫描线。

如图：(图片还是来自网络)~~(我不会画)~~

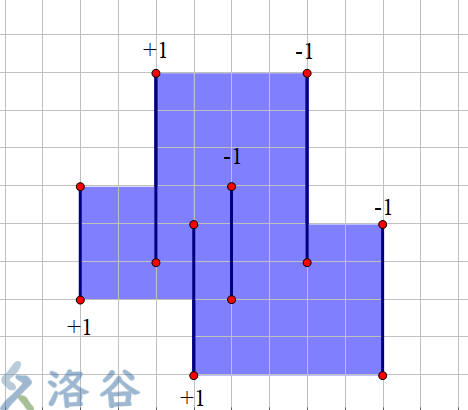
从左往右扫，记录每一条竖直方向上的线段(x表示该线段的横坐标；yl表示该线段下顶点的纵坐标；yh表示该线段上顶点的纵坐标；k为加减的标记(一个矩形先被扫到的线段即左边界为+1、后被扫到即右边界为-1))。
之后，就可以进行离散化了，毕竟1e9的区间长度开线段树不现实。需要离散化的就是每条线段的y坐标上界yh和y坐标下界yl,先把它们的值存在一个临时数组里，再把yl和yh的值都扔进一个val数组，最后把yl和yh的值离散成它们的值在val数组里的下标。

离散化部分：

sort(y + 1, y + n + 1);
cnt = unique(y + 1, y + n + 1) - y - 1;//离散化基本操作
for(register int i = 1; i <= n; i++){
	int pos1 = lower_bound(y + 1, y + cnt + 1, len[i].yl) - y;
       	//查找yl的位置
	int pos2 = lower_bound(y + 1, y + cnt + 1, len[i].yh) - y;
        //查找yh的位置
	val[pos1] = len[i].yl;
	val[pos2] = len[i].yh;
        //把它们的值扔进val数组里
	len[i].yl = pos1;
	len[i].yh = pos2;
        //离散成对应坐标
}

在经过离散化之后，线段树维护的区间端点l,r的含义也发生了变化，变成了区间(\(val[l]\),\(val[r]\))。
再往后，需要对这些线段进行排序，肯定要让x值小的先被扫到。

这样，就形成了上图。

那还有问题吗？显然有啊(废话)

如果，线段树中\(l=r\)的时候，代表区间\((val[l],val[l])\)，变成了一个点。
不妨假设总区间为\([1,4]\)，有一条扫描线\(yl=val[1]\),\(yh=val[3]\)。
加入线段树，修改值。
修改\(bt[1,2]\)长度为\(val[2]-val[1]\)。
修改\(bt[3,3]\)长度为\(val[3]-val[3]=0\)。

欸嘿？\(bt[3,3]\)应该被修改为\(val[3]-val[2]\)才对。
仿佛需要改变线段树储存的值的意义。

用\(l\)表示左区间\(l\)，值为\(val[l]\)；
用\(r\)表示右区间\(r+1\)，值为\(val[r+1]\)；
再看之前的例子，\(yl=val[1]\),\(yh=val[3]\)。
修改\(bt[1,2]\)长度为\(val[2+1]-val[1]\)。
这样就没问题了。

最后摘抄一段蓝皮书上的话：
对于每一个\((x,y1,y2,k)\)，我们再\([val(y1),val(y2)-1]\)上执行期间修改。该区间被线段树划分成 log n个节点，我们把这些节点的\(cnt\)都加\(k\)。

对于线段树中任意一个节点\([l,r]\)，若\(cnt>0\)，则\(len\)等于\(raw(r+1)-raw(l)\),否则，该点\(len\)等于两个子节点的\(len\)之和。在一个节点的\(cnt\)被修改，以及线段树从下往上传递信息时，我们都按照该方法更新\(len\)值。根节点的\(len\)值就是整个扫描线上被覆盖的长度

Code

//从左向右扫
#include<cstdio>
#include<algorithm>

using namespace std;

const int MAX = 1e6+10;
int n, tot, cnt;
long long ans;
long long val[MAX << 1], y[MAX << 1];

struct Tree{
	int l, r;//左右区间  
	int cnt;//该节点自身被覆盖的次数 
	int len;//该节点代表的区间被矩形覆盖的长度 
}bt[MAX << 2];

struct Line{
	long long x;//竖线的横坐标 
	long long yh, yl;//yh:竖线的上端点的纵坐标; yl:竖线的下端点的纵坐标 
	long long sit;//记录该竖线是矩形的左边界还是右边界  
}len[MAX << 1];//记录每条竖线 

inline long long read(){
	long long x = 0, f = 1;
	char c = getchar();

	while(c < '0' || c > '9'){
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = (x << 3) + (x << 1) + (c ^ 48);
		c = getchar();
	}

	return x * f;
}

inline bool cmp(const Line &a, const Line &b){
	return a.x < b.x;
}//依据每条线段x坐标的大小排序 

inline int lson(int x){
	return x << 1;
}

inline int rson(int x){
	return x << 1 | 1;
}

inline void pushup(int rt){
	if(bt[rt].cnt)
		bt[rt].len = val[bt[rt].r + 1] - val[bt[rt].l];
	else
		bt[rt].len = bt[lson(rt)].len + bt[rson(rt)].len;
}//向上更新节点  

void build(int rt, int l, int r){
	bt[rt].l = l;
	bt[rt].r = r;
	bt[rt].cnt = 0;
	bt[rt].len = 0;
	//最初，被覆盖的次数和长度都为0  

	if(l == r)
		return;//叶子节点没有意义，直接退出  

	int mid = (l + r) >> 1;
	build(lson(rt), l, mid);
	build(rson(rt), mid + 1, r);
}

void update(int rt, int l, int r, int data){
	if(bt[rt].l >= l && bt[rt].r <= r){
		bt[rt].cnt += data;
		pushup(rt);//注意在这里也要更新 
		return;
	}

	int mid = (bt[rt].l + bt[rt].r) >> 1;
	if(l <= mid) update(lson(rt), l, r, data);
	if(r > mid) update(rson(rt), l, r, data);

	pushup(rt);
}

int main(){
	n = read();
	for(register int i = 1; i <= n; i++){
		long long x1, y1, x2, y2;
		x1 = read(), y1 = read(), x2 = read(), y2 = read();
		len[(i << 1) - 1].x = x1, len[i << 1].x = x2;
		len[(i << 1) - 1].yl = len[i << 1].yl = y1;
		len[(i << 1) - 1].yh = len[i << 1].yh = y2;
		len[(i << 1) - 1].sit = 1/*左边界*/, len[i << 1].sit = -1;/*右边界*/
		y[++tot] = y1;
		y[++tot] = y2;//存入临时数组，准备离散化 
	}

	n <<= 1;//n*2方便下边操作 
	sort(y + 1, y + n + 1);
	cnt = unique(y + 1, y + n + 1) - y - 1;//去重 
	for(register int i = 1; i <= n; i++){
		int pos1 = lower_bound(y + 1, y + cnt + 1, len[i].yl) - y;//查找yl的位置
		int pos2 = lower_bound(y + 1, y + cnt + 1, len[i].yh) - y;//查找yh的位置
		val[pos1] = len[i].yl;
		val[pos2] = len[i].yh;//把它们的值扔进val数组里
		len[i].yl = pos1;
		len[i].yh = pos2;//离散成对应坐标
	}
	sort(len + 1, len + n + 1, cmp);//按x坐标升序排序 
	build(1, 1, n);
	for(register int i = 1; i < n/*最后一条线段之后肯定不跟着另一条线段，它肯定对最后结果没有贡献*/; i++){
		update(1, len[i].yl, len[i].yh - 1, len[i].sit);//区间加 
		ans += bt[1].len * (len[i + 1].x - len[i].x);//根节点的len值*与下一条线段的距离=这一块内的矩形面积 
	}

	printf("%lld", ans);

	return 0;
}

//换个方法，从上往下扫
#include<cstdio>
#include<algorithm>

using namespace std;

const int MAX = 1e6+10;
int n, tot, cnt;
long long ans;
long long val[MAX << 1], x[MAX << 1];

struct Tree{
	int l, r;  
	int cnt; 
	int len;
}bt[MAX << 2];

struct Line{
	long long y;
	long long l, r;
	long long sit; 
}len[MAX << 1];

inline long long read(){
	long long x = 0, f = 1;
	char c = getchar();

	while(c < '0' || c > '9'){
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = (x << 3) + (x << 1) + (c ^ 48);
		c = getchar();
	}

	return x * f;
}

inline bool cmp(const Line &a, const Line &b){
	return a.y > b.y;
}

inline int lson(int x){
	return x << 1;
}

inline int rson(int x){
	return x << 1 | 1;
}

inline void pushup(int rt){
	if(bt[rt].cnt)
		bt[rt].len = val[bt[rt].r + 1] - val[bt[rt].l];
	else
		bt[rt].len = bt[lson(rt)].len + bt[rson(rt)].len;
} 

void build(int rt, int l, int r){
	bt[rt].l = l;
	bt[rt].r = r;
	bt[rt].cnt = 0;
	bt[rt].len = 0;

	if(l == r)
		return; 

	int mid = (l + r) >> 1;
	build(lson(rt), l, mid);
	build(rson(rt), mid + 1, r);
}

void update(int rt, int l, int r, int data){
	if(bt[rt].l >= l && bt[rt].r <= r){
		bt[rt].cnt += data;
		pushup(rt); 
		return;
	}

	int mid = (bt[rt].l + bt[rt].r) >> 1;
	if(l <= mid) update(lson(rt), l, r, data);
	if(r > mid) update(rson(rt), l, r, data);

	pushup(rt);
}

int main(){
	n = read();
	for(register int i = 1; i <= n; i++){
		long long x1, y1, x2, y2;
		x1 = read(), y1 = read(), x2 = read(), y2 = read();
		len[(i << 1) - 1].y = y1, len[i << 1].y = y2;
		len[(i << 1) - 1].l = len[i << 1].l = x1;
		len[(i << 1) - 1].r = len[i << 1].r = x2;
		len[(i << 1) - 1].sit = -1, len[i << 1].sit = 1;
		x[++tot] = x1;
		x[++tot] = x2; 
	}

	n <<= 1; 
	sort(x + 1, x + n + 1);
	cnt = unique(x + 1, x + n + 1) - x - 1; 
	for(register int i = 1; i <= n; i++){
		int pos1 = lower_bound(x + 1, x + cnt + 1, len[i].l) - x;
		int pos2 = lower_bound(x + 1, x + cnt + 1, len[i].r) - x;
		val[pos1] = len[i].l;
		val[pos2] = len[i].r;
		len[i].l = pos1;
		len[i].r = pos2;
	}
	sort(len + 1, len + n + 1, cmp);
	build(1, 1, n);
	for(register int i = 1; i < n; i++){
		update(1, len[i].l, len[i].r - 1, len[i].sit);
		ans += bt[1].len * (len[i].y - len[i + 1].y);
	}

	printf("%lld", ans);

	return 0;
}

标签：rt,val,int,线段,面积,long,扫描线,模板
来源： https://www.cnblogs.com/TSTYFST/p/16496494.html

【模板】扫描线 面积并