P4474 王者之剑 题解

P4474 王者之剑 题解

前置知识

本题考的是最大权独立集，对于最大权独立集，令最大权独立集的权值之和为 \(|V|\)，最小权覆盖集的权值之和为 \(|R|\)，原图总权值之和为 \(|W|\)，则满足下列公式：

\[|V| = |W| - |R| \]

\(|W|\) 很好求，而 \(|R|\) 的值就是最小割的值，跑一边最大流即可。

对于证明，用反证法很好证：

如果我们选择一个点覆盖集 \(V_1\)，那么它的补集 \(V_2=V-V_1\) 必定是一个独立集，如果我们假设 \(V_2\) 不是一个独立集，那么 \(V_2\) 中必定有一条边的两个端点都在 \(V_2\) 中，因为 \(V_1\) 和 \(V_2\) 互补，则可以推出 \(V_1\) 中必定有一条边的两个端点都不在 \(V_1\) 中，这与 \(V_1\) 是点覆盖集矛盾，结论获证。

同理，用同样的方法，假设一个独立集的不补集不是点覆盖集，证明过程极其相似，不再赘述。

综上所述，即可证明 \(|V| = |W| - |R|\)。

建模

从题目背景里面应得到两个非常重要的结论：

1. 只能在偶数秒拿宝石
2. 不可能同时拿走相邻的宝石

其中第 2 条暗示我们这是一个最大权独立集的问题。对于任意 \(n \times m\) 的图，我们对其染色，如下图：

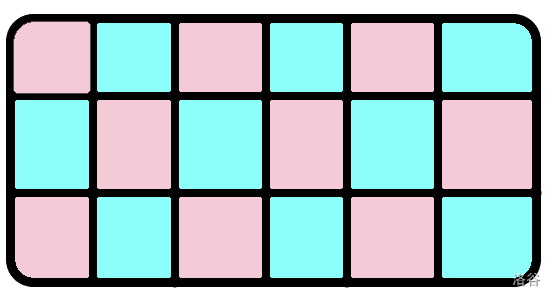
每一个浅蓝格子向周围四个浅粉格子连容量为 \(+ \infty\) 的边，可以保证相邻两个格子里的钻石不可能同时取，因为正常的最小割不可能为 \(+ \infty\) 。

因为可以原地等待，所以原问题的每一种情况我们都可以通过相当的方法在建立的图中找到合法方案；我们建的每一个图也可以对应每一个实际问题，所以我们建的图和原问题是一一对应的（这一点很重要，这样才能保证我们建的图是正确的），最后直接跑一个最大流输出答案即可。

Code

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = 60010, INF = 1e8;

int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], depth[N], cur[N];

int get_idx(int x, int y)
{
	return (x - 1) * m + y;
}

void add(int a, int b, int c)
{
	e[idx] = b;
	f[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
	
	e[idx] = a;
	f[idx] = 0;
	ne[idx] = h[b];
	h[b] = idx ++ ;
	
	return;
}

bool bfs()
{
	int hh = 0, tt = 0;
	memset(depth, -1, sizeof depth);
	q[0] = S;
	depth[S] = 0;
	cur[S] = h[S];
	
	while (hh <= tt)
	{
		int t = q[hh ++ ];
		for (int i = h[t]; ~i; i = ne[i])
		{
			int ver = e[i];
			if (depth[ver] == -1 && f[i] > 0)
			{
				depth[ver] = depth[t] + 1;
				cur[ver] = h[ver];
				q[ ++ tt] = ver;
				if (ver == T) return true;
			}
		}
	}
	
	return false;
}

int dfs(int u, int lmt)
{
	if (u == T) return lmt;
	int flow = 0;
	for (int i = cur[u]; ~i && flow < lmt; i = ne[i])
	{
		cur[u] = i;
		int ver = e[i];
		if (depth[ver] == depth[u] + 1 && f[i] > 0)
		{
			int t = dfs(ver, min(f[i], lmt - flow));
			if (!t) depth[ver] = -1;
			f[i] -= t;
			f[i ^ 1] += t;
			flow += t;
		}
	}
	
	return flow;
}

int dinic()
{
	int res = 0, flow = 0;
	while (bfs())
		while (flow = dfs(S, INF))
			res += flow;
	return res;
}

int main()
{
	cin >> n >> m;
	S = 0, T = n * m + 1;
	memset(h, -1, sizeof h);
	
	int dx[] = {-1, 0, 1, 0};
	int dy[] = {0, 1, 0, -1};
	
	int tot = 0;
	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
		{
			int w;
			cin >> w;
			if ((i + j) & 1)
			{
				add(S, get_idx(i, j), w);
				for (int k = 0; k < 4; k ++ )
				{
					int x = i + dx[k];
					int y = j + dy[k];
					if (x >= 1 && x <= n && y >= 1 && y <= m)
						add(get_idx(i, j), get_idx(x, y), INF);
				}
			}
			else
				add(get_idx(i, j), T, w);
			tot += w;
		}
	
	cout << tot - dinic() << endl;
	return 0;
}

后语

真道题建模真的很有意思诶！还有…… 双倍经验P2774

标签：ver,idx,int,题解,P4474,depth,之剑,return,flow
来源： https://www.cnblogs.com/LittleMoMol-kawayi/p/solution-LuoGu-P4474.html