UVA1660 电视网络 Cable TV Network 题解

UVA1660 电视网络 Cable TV Network 题解

思路

“最少删除多少个点，使得图不连通”，这种描述和最小割极其相似，只不过唯一一点不同的是：这个删的是点，最小割删的是边。

思考一下，能不能把最小割删的边对应到点上呢，很自然可以想到，拆点！想到这里这个题就是个模板题了。

对于拆点，具体而言是将一个点拆成两点一边（如图甲），而此题让求最少删除点的数量，那么就让拆出来的“边”的权值为 1（如图乙）。如果最小割的一个割边是某一个拆出的“边”，其含义就是拆前的点被删掉了。

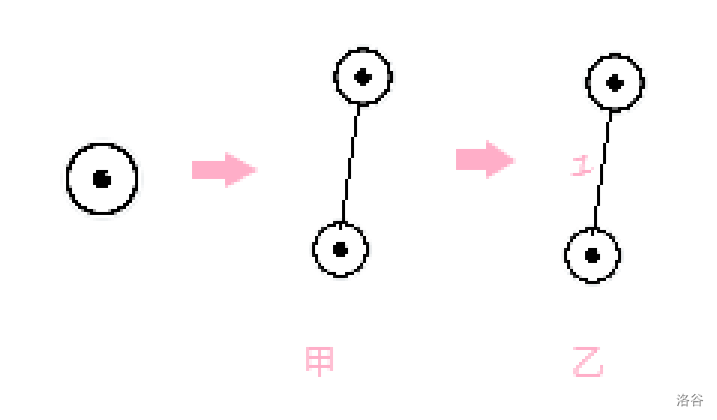
不过还有一个问题，我们必须保证：对于任意一个割边，它必须是某一个所拆出的“边”。因为如果一个割边不是某点所拆出“边”，那么其含义就变成了删掉当前边，这就不符合题意了。这个问题也好解决，将所有拆出来的“边”的权值设为 1 的基础下，其他边的权值设为 \(+ \infty\) ，这样就能保证最小割一定在边权为 \(1\) 的边上了 (不然最小割就成了 \(+ \infty\))。

最后考虑源点和汇点选取问题，由于 \(n \le 50\)，自然想到暴力枚举，枚举源点和汇点的编号，每一种情况下都跑一边最大流，最后取最小值即为答案。

细节

1. 因为拆点过程点一分为二，所以最大点数应为 \(50 \times 2\)。
2. 当原图是完全图时，边数最大；每个点拆点过程中会多出 1 条边，最多有 50 个点；我们维护的是残留网络，所以总边数要乘以 2，所以最终计算最多条边的式子就为 \((50 \times 50 + 50) \times 2\)。
3. 由于是多组测试数据，每次需要还原残留网络，操作为：正向边的剩余权值（容量）加上反向边的剩余权值（流量），反向边的流量设为 0。
4. 输入稍稍恶心，不过用 scanf 就很方便。

Code

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 110, M = 5210, INF = 1e8;

int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], depth[N], cur[N];

void add(int a, int b, int c)
{
	e[idx] = b;
	f[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
	
	e[idx] = a;
	f[idx] = 0;
	ne[idx] = h[b];
	h[b] = idx ++ ;
	
	return;
}

bool bfs()
{
	int hh = 0, tt = 0;
	memset(depth, -1, sizeof depth);
	q[0] = S;
	depth[S] = 0;
	cur[S] = h[S];
	
	while (hh <= tt)
	{
		int t = q[hh ++ ];
		for (int i = h[t]; ~i; i = ne[i])
		{
			int ver = e[i];
			if (depth[ver] == -1 && f[i] > 0)
			{
				depth[ver] = depth[t] + 1;
				cur[ver] = h[ver];
				q[ ++ tt] = ver;
				if (ver == T) return true;
			}
		}
	}
	
	return false;
}

int dfs(int u, int lmt)
{
	if (u == T) return lmt;
	int flow = 0;
	for (int i = cur[u]; ~i && flow < lmt; i = ne[i])
	{
		cur[u] = i;
		int ver = e[i];
		if (depth[ver] == depth[u] + 1 && f[i] > 0)
		{
			int t = dfs(ver, min(f[i], lmt - flow));
			if (!t) depth[ver] = -1;
			f[i] -= t;
			f[i ^ 1] += t;
			flow += t;
		}
	}
	
	return flow;
}

int dinic()
{
	int res = 0, flow = 0;
	while (bfs())
		while (flow = dfs(S, INF))
			res += flow;
	return res;
}

int main()
{
	while (cin >> n >> m)
	{
		memset(h, -1, sizeof h);
		idx = 0;
		for (int i = 0; i < n; i ++ ) add(i, n + i, 1);
		while (m -- )
		{
			int a, b;
			scanf(" (%d,%d)", &a, &b);
			add(n + a, b, INF);
			add(n + b, a, INF);
		}
		
		int ans = n;
		for (int i = 0; i < n; i ++ )
			for (int j = 0; j < i; j ++ )
			{
				S = n + i, T = j;
				for (int k = 0; k < idx; k += 2)
				{
					f[k] += f[k ^ 1];
					f[k ^ 1] = 0;
				}
				ans = min(ans, dinic());
			}
		cout << ans << endl;
	}
	
	return 0;
}

完结撒花~

标签：ver,Network,idx,int,题解,Cable,flow,50,depth
来源： https://www.cnblogs.com/LittleMoMol-kawayi/p/solution-LuoGu-UVA1660.html