blocks(昆明ICPC)
作者:互联网
链接:https://ac.nowcoder.com/acm/contest/32708/B
必须得感叹一下这个题真的牛
分析:发现n很小 所以能覆盖完的情况是能枚举出来的 第一个问题就来了
怎么判断状态s能否将整个区域覆盖完全 不难想到求出覆盖面积 合并面积不好算 交面积好算 所以用到容斥原理
面积=Σ一个矩形面积 - Σ两个矩形相交的面积 + Σ三个矩形相交的面积 - .... 这里的面积都是在指定区域内的面积 如果没相交则面积为0
枚举状态i的所有子集
for (int s = i; s; s = (s - 1) & i)
考虑S的子集,在二进制上从大到小排成一排,那么大的通过减若干个1就一定能到小的,
但是中间会产生大量的状态,这些状态中包含了一些S中不包含的1,故和S&一下,去冗即可,
接下来就是求期望步数
期望倒推 设dp[i]表示当前状态为i 还需多少步才能将所有覆盖
转移有两种
(1)下一步选的已经出现过 cnt/n × dp[i] 其中cnt为状态i中1的个数
(2)下一步选的还未出现过 Σ(1/n × dp[i|1<<j])
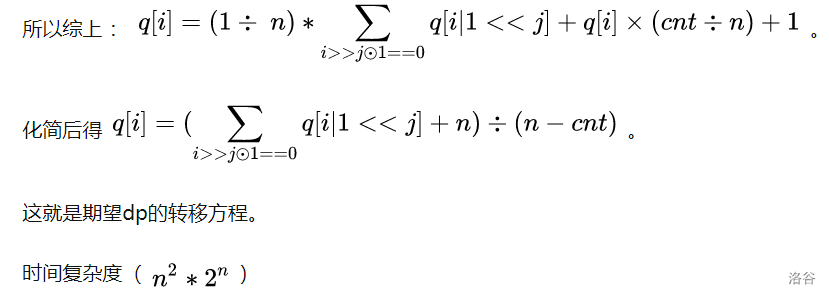
code:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 15;
const ll mod = 998244353;
ll n, w, h;
ll x[N], y[N], xx[N], yy[N];
ll dp[1 << 11 + 10], area[1 << 11 + 10], q[1 << 11 + 10];
ll qpow(ll a, ll b)
{
ll ans = 1;
while (b)
{
if (b & 1)
{
ans = ans * a % mod;
}
a = a * a % mod;
b >>= 1;
}
return ans;
}
void solve()
{
cin >> n >> w >> h;
for (int i = 0; i < n; i++)
{
cin >> x[i] >> y[i] >> xx[i] >> yy[i];
}
for (int i = 1; i < (1 << n); i++)
{
ll x1 = 0, y1 = 0, x2 = w, y2 = h;
for (int j = 0; j < n; j++)
{
if (i >> j & 1)
{
x1 = max(x1, x[j]);
x2 = min(x2, xx[j]);
y1 = max(y1, y[j]);
y2 = min(y2, yy[j]);
}
}
area[i] = max(0ll, x2 - x1) * max(0ll, y2 - y1); //枚举上界和下界求矩形面积交
}
for (int i = 1; i < (1 << n); i++)
{
dp[i] = 0;
for (int s = i; s; s = (s - 1) & i)
{
dp[i] += area[s] * (__builtin_parity(s) ? 1 : -1); //容斥求矩形面积并////__builtin_parity(i)库函数返回二进制中1的个数的奇偶性,奇数返回1,偶数返回0
}
}
ll s = w * h;
if (dp[(1 << n) - 1] != s) //无法涂满矩阵
{
cout << -1 << "\n";
return;
}
for (int i = (1 << n) - 1; i >= 0; i--) //期望dp,式子在上面推过了
{
q[i] = 0;
if (dp[i] == s)
continue;
ll s1 = 0;
for (int j = 0; j < n; j++)
{
if (!(i >> j & 1))
{
s1 = (s1 + q[i | (1 << j)]) % mod;
}
}
q[i] = (n + s1) * qpow(n - __builtin_popcount(i), mod - 2) % mod; //__builtin_popcount(i)库函数返回二进制中1的个数
}
cout << q[0] << "\n";
}
int main()
{
ll t;
cin >> t;
while (t--)
{
solve();
}
}
标签:blocks,int,max,ll,面积,ICPC,昆明,矩形,dp 来源: https://www.cnblogs.com/wzxbeliever/p/16484848.html