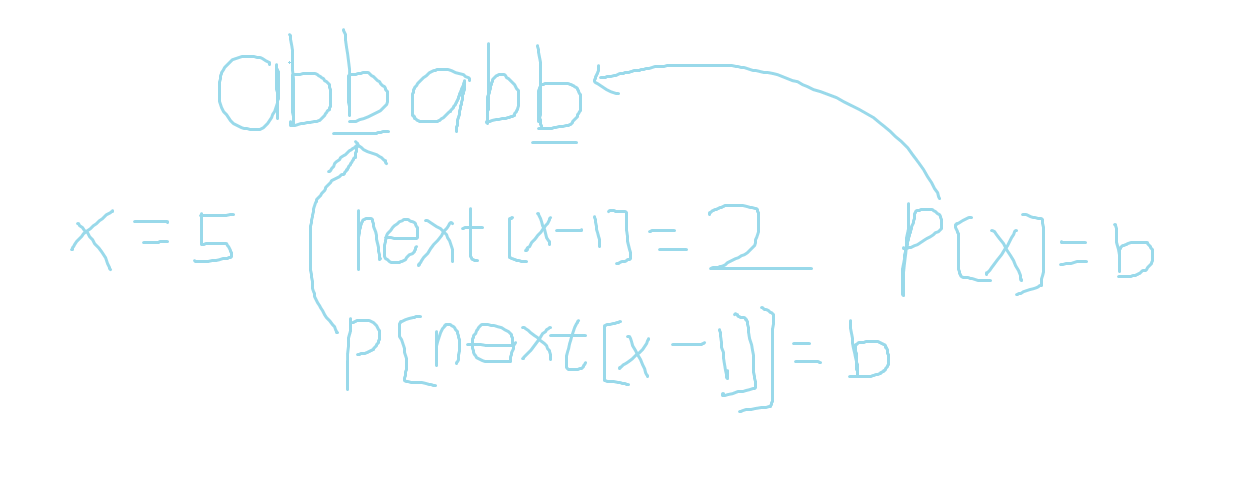数据结构学习笔记
作者:互联网
数据结构=个体的存储+个体的关系存储
算法=对存储数据的操作
数据结构是专门研究数据存储的问题
狭义的算法是与数据的存储方式密切相关;广义的算法是与数据的存储方式无关
一.指针
CPU无法直接访问硬盘,只能直接访问内存,故若想要访问硬盘中的数据,先要将硬盘中的内容转移到内存中去。
内存中也分为一个一个的小格子,并且带有编号,从0、1、2一直到4G-1。(内存分页机制)
CPU与内存之间可看作由3根线进行控制。地址线、控制线、数据线。地址线负责地址的操作,控制线负责控制是读数据还是写数据、数据线负责数据的传输。
地址就是内存单元的编号 从0开始的非负整数 范围为从0-FFFFFFFF(0-4G-1)
指针就是地址 地址就是指针 指针变量就是存放内存单元地址的变量 指针的本质就是一个操作受限的非负整数
指针不能不初始化,否则会乱指,无法编译通过。
分类:
1.基本类型的指针
2.指针和数组的关系
int i=10;
int *p=&i; //等价于 int *p; p=&i
详解上述两步操作:
1.p定义为一个整型指针,故只能存放整形变量的地址。p存放了i的地址,所以我们说o指向了i。
2.p和i是完全不同的两个变量,修改其中任意一个变量的值不影响另一个变量的值。
3.p指向i,*p就是i变量本身。
总结: 1、如果一个指针变量存放了一个普通变量的地址,这个指针变量就可以说指向了这个变量,但其实二者是两个完全不同的变量,修改其中一个变量的值不影响另一个变量的值。
2、p等价于i,p可以与i在任何地方互换。
3、如果一个指针变量指向了某个普通变量,则*指针变量就完全等价于该普通变量。
指针变量也是变量,只不过他存放的不能是内存单元的内容,而只能存放内存单元的地址。
普通变量前不能加* 常量和表达式前不能加&
通过被调函数修改主调函数中参数的值
1、实参为相关变量的地址 2、形参为以该变量的类型为类型的指针 3、在被调函数中通过 *形参变量名 的方式就可以修改主函数相关变量的值。
#include <stdio.h>
void function(int i){
i=100;
}
int main(){
int i=9;
f(i);
printf("i=%d\n",i);
return 0;
}
//i还是9
#include <stdio.h>
void function(int *i){
*i=100;
}
int main(){
int i=9;
f(&i);
printf("i=%d\n",i);
return 0;
}
//此时将main中i的地址发送给了function中的*i,即i指向了function中的i,*i就代表了function中的i的值,所以输出i的值将会等于100.
指针和数组
#include <stdio.h>
int main(){
int a[5]={1,2,3,4,5}; //1,2,3,4,5不是在a中进行存放的,
return 0;
}
一维数组名是个指针常量,它存放的是一维数组第一个元素的地址,且值不能被改变。
一维数组名指向的是数组的第一个元素。数组中连续单元的内存地址是连续的,int型占4个字节,相邻元素地址就差4. 以此类推。
下标和指针的关系
a[i]==*(a+i) a[0]=*(a+0)
假设指针变量的名字为p,则p+i的值是p+i*(p所指向的变量所占的字节数)
如果a所指向的是一个占用了8字节的变量,那么*a+1所开辟的新空间也会是8个字节,去储存所代表的变量,这是编译器自动去计算的,
指针变量的运算:
指针变量不能相加,不能相乘,不能相除。 如果两指针变量属于同一数组,则可以相减
指针变量可以加减一整数,前提是最终结果不能超过指针
#include <stdio.h>
void Show_Array(int *p,int len){
p[2]=-1;
}
int main(){
int a[5]={1,2,3,4,5};
Show_Array(a,5);//a等价于&a[0],&a[0]本身代表int *类型
printf("%d\n",a[2]);
return 0;
}
p+i的值是p+i*(p所指向的变量所占的字节数)
p-i的值是p-i*(p所指向的变量所占的字节数)
p++ 就代表是p+1 p--就代表是p-1
#include <stdio.h>
int main(){
double *p;
double x=66.6;
p=&x;// x占八个字节 一个字节是八位 一个字节一个地址 p所存放的是八个地址中的首地址,只存放一个地址
double arr[3]={1.1,2.2,3.3};
double *q;
q=arr;
printf("%p",q);
printf("%p",q+1);
return 0;
}
无论一个指针变量指向的变量占用多少个字节,指针变量都统一占用四个字节。
通过其他函数改变函数内部的数值:
#include <stdio.h>
void f(int *p);
void f(int *p){
*p=99;
}
int main(){
int i=10;
f(&i);
printf("%d\n",i)
return 0;
}
结构体:
结构体变量不能加减乘除,但可以相互赋值。
二.动态内存的分配和释放
#include "stdio.h"
#include "stdlib.h"
int main(){
int len;
scanf("%d",&len);
int *pArr=(int *)malloc(sizeof(int)*len); //pArr是第一个元素的地址,可以当作是数组名即可
*pArr=4//类似于a[0]=4
pArr[1]=10;//类似于a[1]=10
free(pArr);//吧pArr所代表的动态分配的20个字节内存释放 昨晚上太晚了,20个字节是上面len=5的情况下
return 0;
}
跨函数使用内存
当一个函数执行完毕时,其内部分配的局部变量的内存将会被释放,也就是说,函数执行的语句结束后,其内部的局部变量都将不存在,指针所指向的变量也会不存在。
而我们主动使用malloc动态分配的内存必须手动释放才会消失,不像上述提到的会自动释放掉,所以C和C++一大缺点就是缺少垃圾回收机制,内存不会自动释放,容易导致内存泄漏的问题发生。
三.线性存储结构(可以当作像糖葫芦一样用一根线穿起来的):
3.1连续存储
数据分为线性存储和非线性存储。非线性存储包括树和图。
数组和广义表可以看作是线性结构的推广
线性结构则分为(将所有的结点用一根直线穿起来):
连续存储[数组]
离散存储[链表]
1.数组[连续存储]
i>什么叫数组
具有相同类型的数据元素的集合
II>数组的优缺点
优点:
1.存取的速度很快,效率非常高
缺点:
1.插入删除元素很慢(当你要插入删除元素时,就会因为要保证下标的变化,使得其他所有元素都要发生改变)
2.空间有限制,需要大块连续的内存块
3.事先必须知道数组的长度
二维数组:
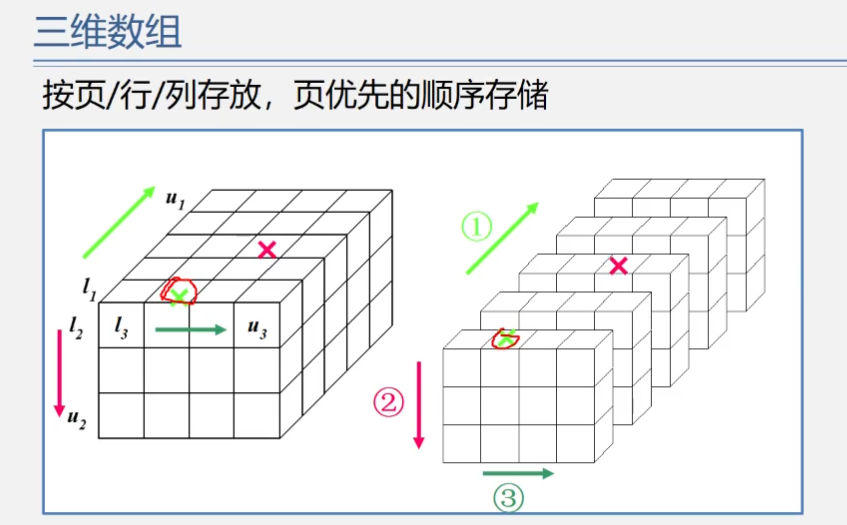
数组的顺序存储:
如何判断以这样存储的元素被压缩到一维数组的哪个位置了呢?
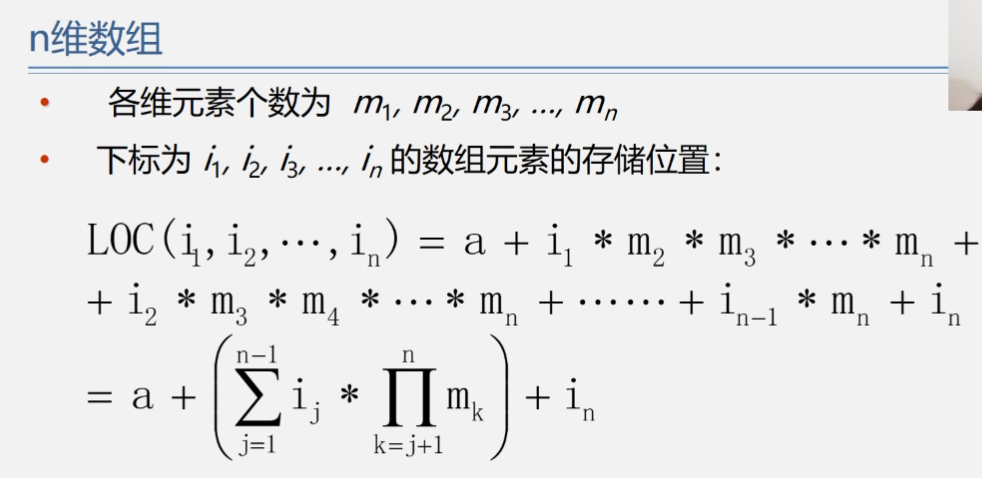
假设二维数组中的元素aij被压缩,那么这个元素之前应该有i-1行,所以行数就是等差数列求和,从1一直加到i-1,最后我们还需要再加上这个元素同一行的前面的元素个数,也就是j-1个元素,最后将二者结果相加即可得到在一维数组中的下标k
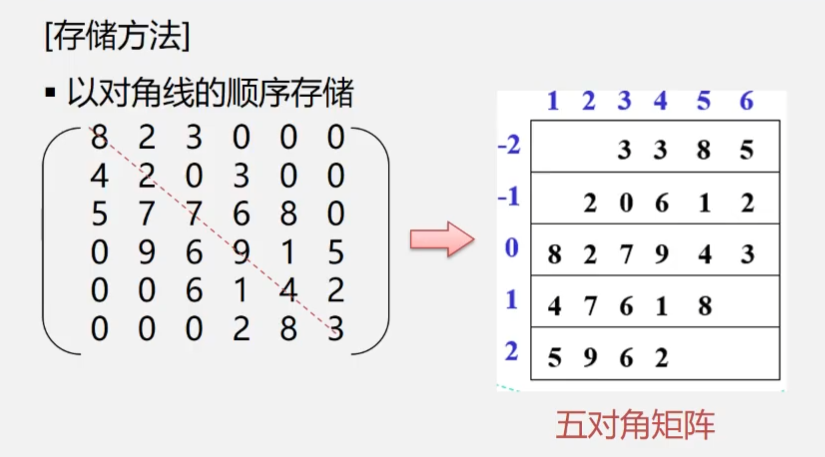
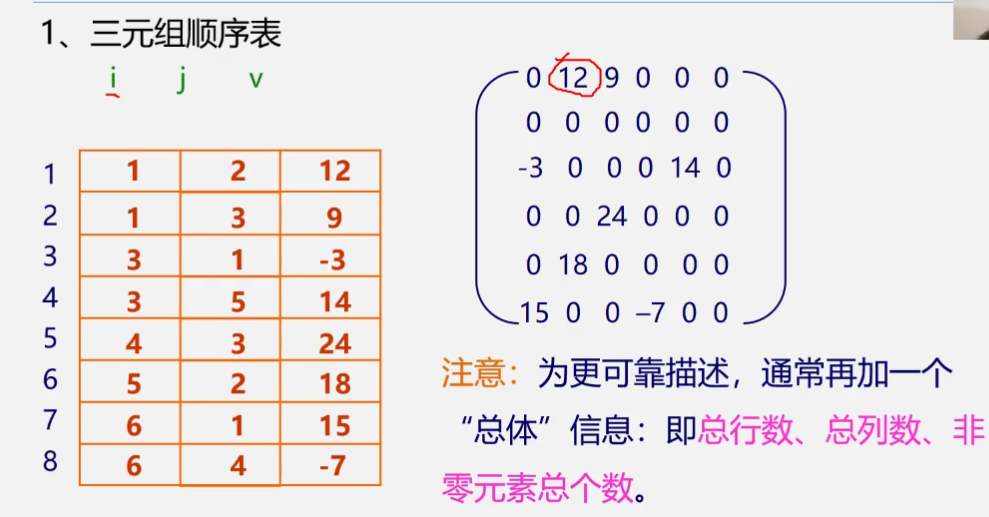
我们以对角线的顺序来存储对角矩阵,并使用二维数组进行存放(当然一维数组也不是不行),五对角矩阵的含义就是矩阵中有五条对角线上有非零元素,其他元素都为零
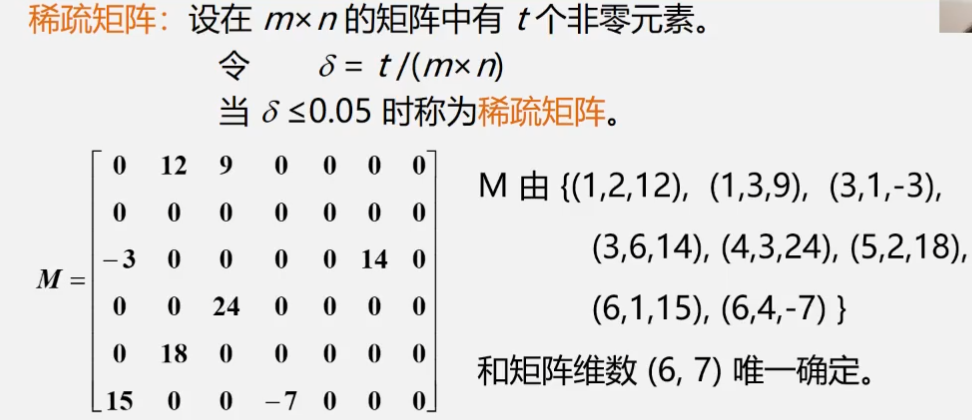
对于稀疏矩阵,我们利用三元组法来确定矩阵,三元组法形式为(i,j,aij),i和j为元素所在的行和列,aij代表元素本身
我们还可以再添加一个下标为0的行,存入总行数6,总列数6,以及非零元素个数8
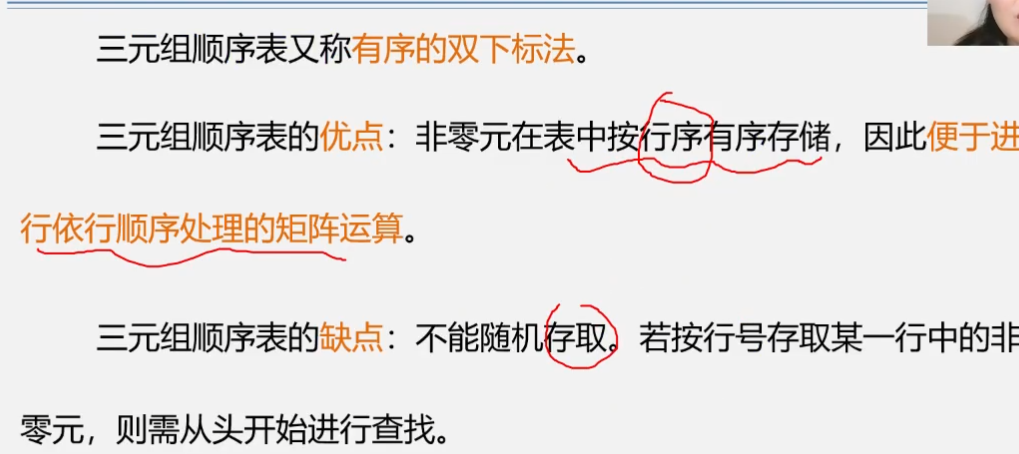
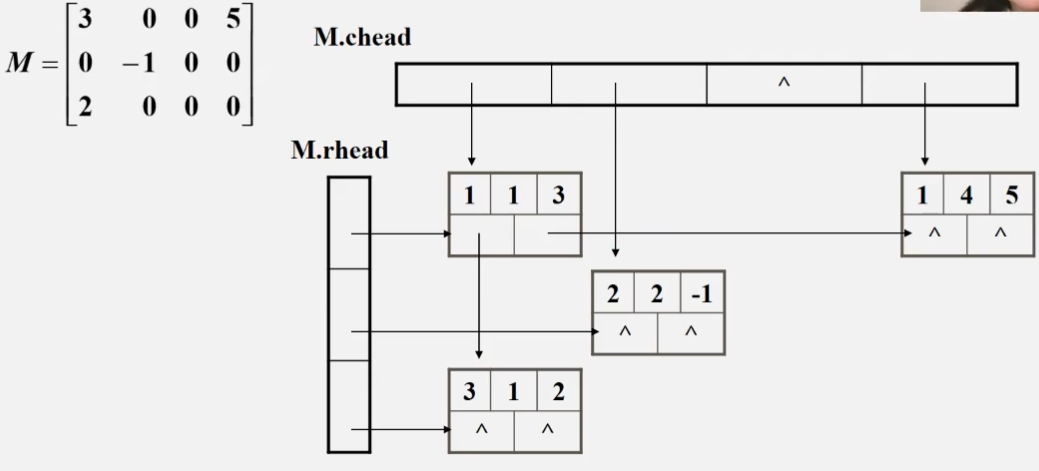
我们可以继续用十字链表的形式来改进三元组顺序表法的缺点
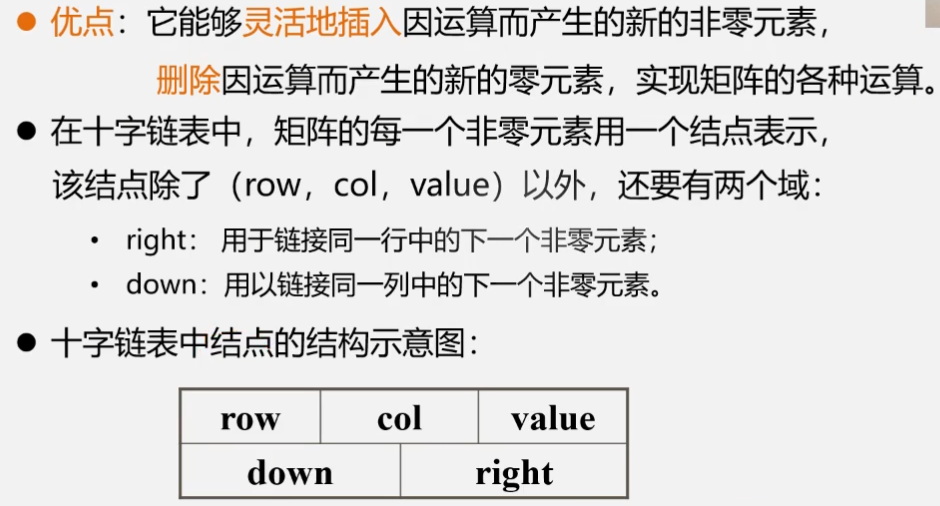
如上图所示,第一行的非零元素a11除按照三元组顺序法进行保存外,还要多存储一个down指针指向同一列中下一个非零元素,其次还有一个right指针指向同一行中下一个非零元素,无法找到的a22就再创建一个新节点就可以了。同时类比链表,为了方便对这些节点进行操作,我们还需要建立头结点,分为r(行)头结点以及c(列),分别指向当前行(列)中第一个非零元素即可
数组功能简单实现:
#include "stdio.h"
#include "stdlib.h"
//我们在此定义了一个数据类型,该类型的名字为struct Arr,该数据类型含有三个成员,分别是pBase、len、cnt
struct Arr{
int * pBase;//数组的第一个元素的地址
int len;//数组的长度
int cnt;//当前数组的有效元素的个数
// int increment;自动增长因子
};
void init_arr(struct Arr *pArr,int length);
bool append_arr(struct Arr * pArr,int val);
bool insert_arr(struct Arr * pArr,int pos,int val); //pos从1开始
bool delete_arr();
int get();
bool is_empty(struct Arr * pArr);
bool is_full();
void sort_arr();
void show_arr(struct Arr *pArr);
void inverse_arr();
void init_arr(struct Arr *pArr,int length){
pArr->pBase=(int *) malloc(sizeof(int)*length);//如果此处内存成功分配,那么就会是分配的值,但如果内存已满无法成功分配,那么就会将NULL分配给pBase
if(NULL==pArr->pBase){
printf("动态内存分配失败!\n");
exit(-1);//表示终止整个程序
}else{
pArr->len=length;
pArr->cnt=0;
}
return;
}
bool is_empty(struct Arr * pArr){
if(0==pArr->cnt)
return true;
else
return false;
}
bool is_full(struct Arr * pArr){
if(pArr->cnt==pArr->len)
return true;
else return false;
}
bool append_arr(struct Arr * pArr,int val){
if(is_full(pArr))
return false;
else{
/* pArr->pBase[0]=1;cnt=1
* pArr->pBase[1]=2;cnt=2
* pArr->pBase[2]=3;cnt=3
* 综上可知 通过试数我们不难发现
* pArr->pBase[cnt]=val;
* ++cnt; cnt的值就是新放入的元素的下标。 ++cnt表示当前有效元素的个数
* */
pArr->pBase[pArr->cnt]=val;
pArr->cnt++;
return true;
}
}
bool insert_arr(struct Arr * pArr,int pos,int val){
int i;
for(i=pArr->cnt-1;i>=pos-1;--i){
pArr->pBase[i+1]==pArr->pBase[i];
}
pArr->pBase[pos-1]=val;
}
void show_arr(struct Arr * pArr){
if(is_empty(pArr)){
printf("您输入的数组为空!\n");
}else{
for(int i=0;i<pArr->cnt;++i){
printf("%d ",pArr->pBase[i]);//pBase存放了数组中第一个元素的地址,所以可当作一个数组变量名来以相同的办法进行使用。
printf("\n");
}
}
}
int main(void){
struct Arr arr;
init_arr(&arr,6);
append_arr(&arr,1);
append_arr(&arr,2);
append_arr(&arr,3);
append_arr(&arr,4);
append_arr(&arr,5);
append_arr(&arr,6);
append_arr(&arr,7);
show_arr(&arr);
return 0;
}
3.2离散存储(任何一个点到其他点之间的间距可以被正确计算出来)
1.链表
定义:n个节点离散分配
彼此通过指针进行相连
每个节点只有一个前驱节点,每个节点只有一个后续节点
首节点没有前驱节点,尾节点没有后续节点
专业术语:
首节点:第一个有效节点
尾节点:最后一个有效节点
头结点:在首节点前面放置一个节点,称为头结点。没有存放有效数据,也没有存放有效节点的个数。加入头结点的原因是可以简便对链表算法的操作。头结点所存放的数据类型和首节点所存放的数据类型是相同的。
头指针:指向头节点的指针变量(并不是指向了首节点)
尾指针:指向尾节点的指针
如果希望通过一个函数对链表进行处理,我们至少需要接受链表的哪些参数:
只需要一个参数:头指针 通过头指针可以找到头结点,推算出链表的其他所有参数,同时因为存放的为地址,削减了空间的占用,而且后续在调用函数输出链表内容时,不必考虑不同链表存储数据类型的不同而无法应用同一函数。
链表的优缺点:
优点:
1.空间没有限制 内存足够大可以一直New节点 但数组强调必须要分配连续的内存,操作系统不一定找得到,限制较大。
2.插入删除元素很快(只需要修改一个节点,其他节点不用动,改改指针指向的结构体变量的指针成员即可)
缺点:
1.存取速度很慢(当你需要找到某个想要的元素时,无法像数组一样直接通过指定下标进行操作,只能从头开始一个个指向下一个节点,直到找到自己想要的那一个)
节点(Node)的建立:
一个节点要包含两部分,一个是当前节点存储的有效数据,一个是指向下一个节点的指针。
前一个节点的指针域指向后一个节点整体。
结构体中的一个成员,指向与他数据类型相同的另一个成员。
#include <stdio.h>
typedef struct Node{
int data;//数据域
struct Node * pNext;//指针域 和本身数据类型相同,但是另一个节点
}NODE *PNODE;//NODE代表struct Node数据类型,而PNODE代表struct Node *数据类型
int main(){
return 0;
}
分类:
单链表:每一个节点只有一个指针域,即指向下一个节点
双链表:每一个节点有两个指针域 前面的指针域指向上一个节点 后面的指针域指向下一个节点
循环链表:能通过任何一个节点找到其他所有的节点
非循环链表:
算法:遍历 查找 清空 销毁 求长度 排序 删除节点 插入节点
如何实现插入节点:
令p所指向的结构体变量的指针指向q,q指向的结构体变量的指针指向下一个结构体即可
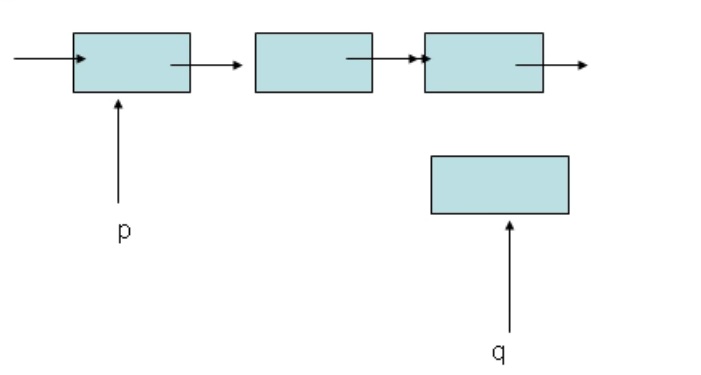
首先p是一个指向节点的指针变量,其并没有指针域,只是p指向的结构体变量具有指针域。
两种实现方式:
#include <stdio.h>
typedef struct Node{
int data;//数据域
struct Node * pNext;//指针域 和本身数据类型相同,但是另一个节点
}NODE *PNODE;//NODE代表struct Node数据类型,而PNODE代表struct Node *数据类型
/*第一种*/
r=p->pNext;p->pNext=q; q->pNext=r;
/*这里使用r的原因和swap时申请一个temp变量有异曲同工之妙,令p所指向的节点指向的下一个为q,完成第一部操作,之后再使q所指向的结构体变量所指向的下一个为r,这里如果在一开始并没有用一个r变量存入p->pNext,此时直接讲p->pNext赋值给q所指向的节点的指针域,此时此刻的p->pNext已经变为q了,成为了自己指向自己,就不正确了*/
/*第二种*/
q->pNext=p->pNext; p->pNext=q;
/*第二种方法个人认为更为巧妙,直接先将p指向的后一个节点赋给q,之后将p指向的变为q即可*/
删除非循环单链表节点

思路:要想删除p节点后面的一个节点,其实只需要将p节点所指向的下一个节点改为下下个节点即可。
伪算法:
#include <stdio.h>
typedef struct Node{
int data;//数据域
struct Node * pNext;//指针域 和本身数据类型相同,但是另一个节点
}NODE *PNODE;//NODE代表struct Node数据类型,而PNODE代表struct Node *数据类型
p->pNext=p->pNext->pNext;
/*乍一看,上面的写法没有问题,p->pNext代表p所指向的结构体变量中的pNext这一成员,即下一个节点,而下一个节点的pNext又指向下一个节点,但实际上这样会导致内存泄漏,即内存越用越少*/
/*正确的写法*/
r=p->pNext;//r代表要删除的那个节点
p->pNext=p->pNext->pNext;
free(r);
typedef struct node
{
int data;
struct node *pNext;
}NODE,*PNODE;
PNODE p=(PNODE)malloc(sizeof(NODE)); //将动态分配的新节点的地址赋给p
free(p);//删除的是p指向节点所占的内存,并不是删除p本身所占内存 p本身所占的内存为栈内存 指向的为堆内存
p->pNext;//p所指向的结构体变量(节点)中的pNext成员本身
链表创建和链表的遍历:
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
typedef struct Node
{
int data;//数据域
struct Node * pNext;//指针域
}NODE,*PNODE;//NODE代表struct Node数据类型,而PNODE代表struct Node *数据类型
PNODE create_list(void);//函数声明
void traverse_list(PNODE pHead);
int main()
{
PNODE pHead=NULL;//等价于 struct Node * pHead =NULL;
pHead=create_list();//create_list()功能: 创建一个非循环单链表,并将该链表的头结点的地址赋给pHead
traverse_list(pHead);
return 0;
}
PNODE create_list(void)//链表的尾插法 链表即使是空的,也是有一个头结点的
{
int len;//用来存放有效节点的个数
int val;//用来临时存放用户输入的结点的值
PNODE pHead = (PNODE) malloc(sizeof(NODE));//创建了一个不存储有效数据的头结点
if(NULL==pHead){
printf("分配失败");
exit(-1);
}
PNODE pTail=pHead;
pTail->pNext=NULL;
scanf("%d",&len);
for(int i=0;i<len;++i){
printf("请输入第%d个节点的值:",i+1);
scanf("%d",&val);
PNODE pNew=(PNODE)malloc(sizeof(NODE));//这里使用一个pNew指向每次循环新建的节点,保证了就算有一万个节点也还是只是用了一个pNew指向了它们
if(NULL==pNew){
printf("分配失败");
exit(-1);
}
pNew->data=val;
pTail->pNext=pNew;
pNew->pNext=NULL;
pTail=pNew;
}
return pHead;
}
void traverse_list(PNODE pHead)
{
PNODE p=pHead->pNext;
while(NULL!=p){
printf("%d",p->data);
p=p->pNext;//将p指针移动至指向之前的p指向的节点的后一个节点
}
printf("\n");
return;
}
判断链表是否为空、求链表长度
bool is_empty(PNODE pHead);
int length_list(PNODE);
bool insert_list(PNODE,int,int);
bool delete_list(PNODE,int,int *);
void sort_list(PNODE);
bool is_empty(PNODE,pHead)
{
if(pHead->pNext==NULL)//头结点为空就行了,不难理解
return true;
else
return false;
}
int length_list(PNODE)
{
PNODE p=pHead->pNext;
int len=0;
while(p!=NULL){
++len;
p=p->pNext;
}
return len;
}
排序链表
void sort_list(PNODE pHead)
{
int i,j,t,len=length_list(pHead);
PNODE p,q;
for(i=0,p=pHead->pNext;i<len-1;++i,p->pNext){
for(j=i+1,q=p->pNext;j<len;++j,q->pNext){
if(p->data>q->data){ //类似数组中的:a[i]>a[j]
t=p->data;//t=a[i]
p->data=q->data;//a[i]=a[j]
q->data=t;//a[j]=t
}
}
}
}
此处引入一个泛型的概念:利用某种技术达到的效果,不同的存储方式,执行的操作相同。
链表的插入和删除算法:
//在pHead所指向的链表的第pos个节点的前面插入一个新的节点,该节点的值是val,pos默认从1开始
bool insert_list(PNODE pHead,int pos,int val)
{
//下面是一种比较高效的写法,不用读取长度,也不用判断是不是空链表。
int i=0;
PNODE p=pHead;
while(NULL!=p&&i<pos-1)//循环结束后,p将指向pos前一个节点
{
p=p->pNext;
++i;
}
if(i>pos-1||NULL==p)//i>pos-1是为了插入位置为负数,NULL=p是为了处理插入位置越界
return false;
PNODE pNew=(PNODE)malloc(sizeof(NODE));//动态分配一个节点的内存出来
if(NULL==pNew)
{
printf("动态分配内存失败\n");
exit(-1);
}
pNew->data=val;
/*插入一个节点
PNODE q=p->pNext;
p->pNext=pNew;
pNew->pNext=q;
*/
/*q->pNext=p->pNext;
p->pNext=q;
另一种实现方式。
*/
return true;
}
bool delete_list(PNODE pHead,int pos,int * pVal)
{
int i=0;
PNODE p=pHead;
while(NULL!=p->pNext&&i<pos-1)
{
p=p->pNext;
++i;
}
if(i>pos-1||NULL==p->pNext)
return false;
PNODE q=p->pNext;//表示要删除的节点 即指针p当前所指向的节点的后一个节点 也即第pos个节点 将头结点当作为第一个节点,默认从1开始读入pos
*pVal=q->data;//利用一个整形指针存放下要删除的节点中曾经所存放的数值 调用前传进一个整型指针
p->pNext=p->pNext->pNext;
free(q);
return true;
}
3.3线性结构的常见应用
1.栈(操作受限的线性表)
#include <stdio.h>
#include <malloc.h>
void f(int k)
{
//m和q都为局部变量,在栈中进行分配
int m;
double *q=(double *)malloc(200);
}
int main(void)
{
//i和p都是局部变量,在栈中进行分配
int i=10;
int * p=(int *)malloc(100);
return 0;
}
//而上述代码中动态分配的200和100并不会随着函数执行完毕后而消失,会一直存在,这两条数据在堆中进行存放,也就是说,我们规定静态分配的在栈中进行分配,而动态分配的在堆中进行分配。栈是由操作系统帮助你进行分配的,而堆则是由程序员们自己去分配的。
定义:一种可以实现”先进后出“的存储结构(先存进去的东西后出来,也就是说,越早出来的东西肯定越晚被放进去)
就类似箱子一样。
队列是一种”先进先出“的存储结构,也就是说,先从队伍中出来的人肯定是先进入队列排队的人。
栈和队列是限定插入和删除只能在表的端点进行的线性表
栈和队列都规定要从尾部插入,栈从尾部删除,队列从头部删除
分类:
静态栈:
动态栈:
算法:
出栈:
压栈:
应用:函数调用
中断
表达式求值
内存分配
缓冲处理
迷宫
栈程序:
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
typedef struct Node
{
int data;
struct Node * pNext;
}NODE,* PNODE;
struct Stack
{
PNODE pTop;//永远指向栈顶元素
PNODE pBottom;//指向栈顶元素下一个没有实际意义的元素
}STACK,*PSTACK;
void init(PSTACK pS)//通过初始化函数先造出一个空栈来,所谓空栈即pTop和pBottom都指向了不存放有效数据的尾结点(栈中在最下层的元素)
{
pS->pTop=(PNODE)malloc(sizeof(NODE));
if(NULL==pS->pTop)
{
printf("动态内存分配失败\n");
exit(-1);
}
else
{
pS->pBottom=pS->pTop;
pS->pTop->pNext=NULL;//清空指针域,此时就相当于在一个空箱子中放入了第一本书,肯定被压在最下面,所以它的下面不会再有书,也就是说指针域为空,不指向其他。
}
}
void push(PSTACK pS,int val)
{
PNODE pNew=(PNODE)malloc(sizeof(NODE));
pNew->data=val;
pNew->pNext=pS->pTop;
pS->pTop=pNew;
return;
}
void traverse(PSTACK pS)
{
//建一个指针,永远指向栈顶元素
PNODE p=pS->pTop;
while(p!=pS->pBottom){
printf("%d",p->data);
p=p->pNext;
}
printf("\n");
return;
}
bool is_empty(PSTACK pS)
{
if(pS->pTop==pS->pBottom){
return true;
}else{
return false;
}
}
//将pS所指向的栈进行出栈操作,并将出栈的元素进行存储
bool pop(PSTACK pS,int * pVal)
{
if(is_empty(pS))
{
return false;
}else
{
PNODE r=pS->pTop;
*pVal=pS->pTop->data;
pS->pTop=pS-pTop->pNext;
free(r);
r=NULL;//避免r指针乱指 因为free之后,r的值就会变成垃圾值,在乱指
return true;
}
}
void clear(PSTACK pS)
{
if(is_empty(pS))
{
return;
}
else
{
PNODE p=pS->pTop;
PNODE q=NULL;
while(p!=pS->pBottom)
{
q=p->pNext;
free(p);
p=q;
}
pS->pTop=pS->pBottom;
}
}
int main()
{
STACK S;
init(&S);//只有传入地址,才能改变值。
push(&S,1);//压栈,在栈中存入新数据时无需指定位置,因为栈就和箱子一样,你只能每次在最上方放入新的数据,也就说,其实不难发现,pBottom一般情况下不会改变,每进行一次压栈时,pTop都会改变,指向新压入的节点。
push(&S,2);
push(&S,3);
push(&S,4);
pop(&S,*val);
traverse(&S);//遍历输出
return 0;
}
2.队列(操作受限的线性表)
定义:
一种可以实现“先进先出”的存储结构
分类:
链式队列(内部是链表,我们对链表进行操作)
静态队列(内部是数组来实现),一般都用循环队列
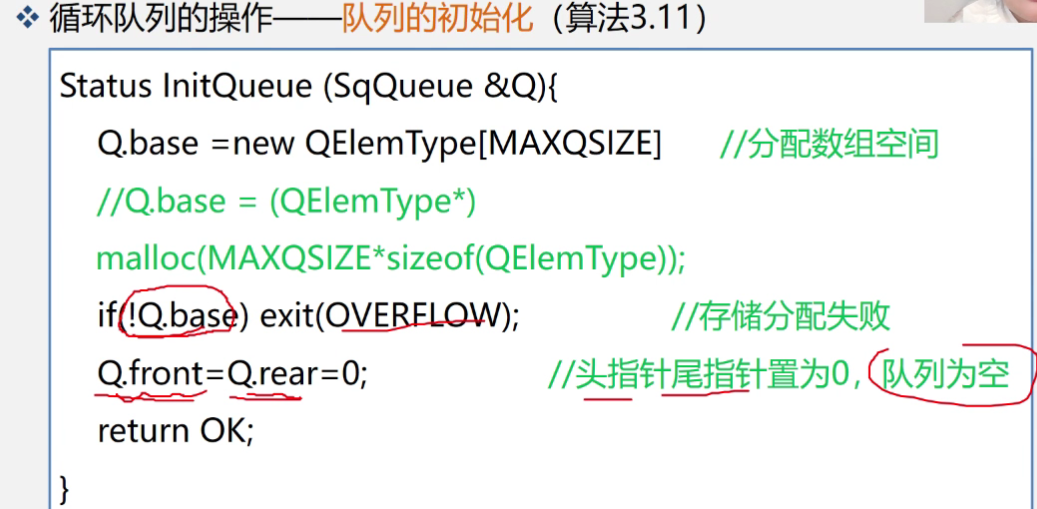
何为循环队列:
· 静态队列为什么必须是循环队列
· 循环队列需要几个参数来确定
· 循环队列各个参数的含义
· 循环队列入队伪算法讲解
· 循环队列出队伪算法讲解
· 如何判断循环队列是否为空
· 如何判断循环队列是否已满
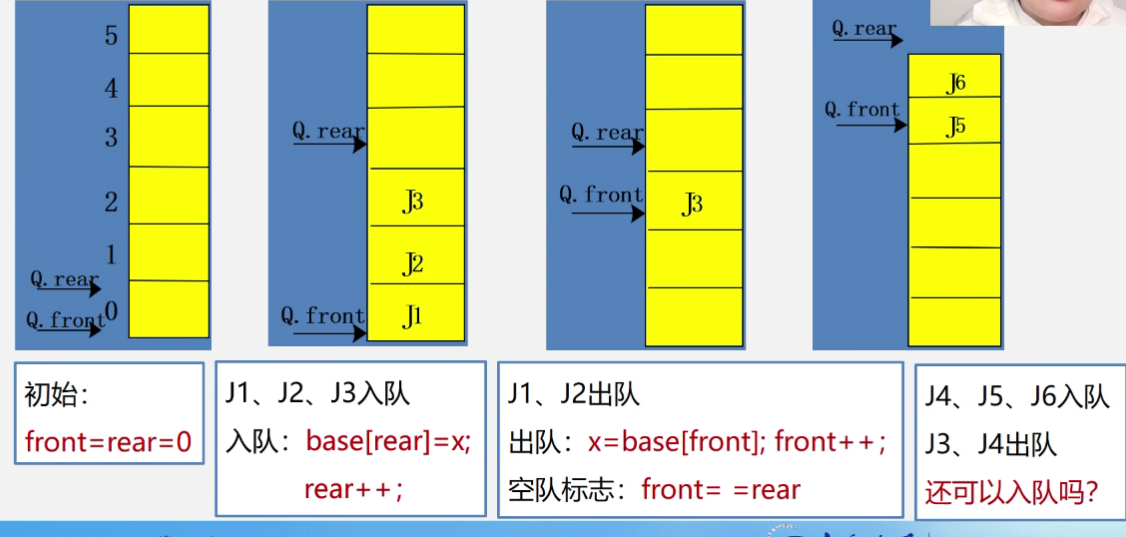
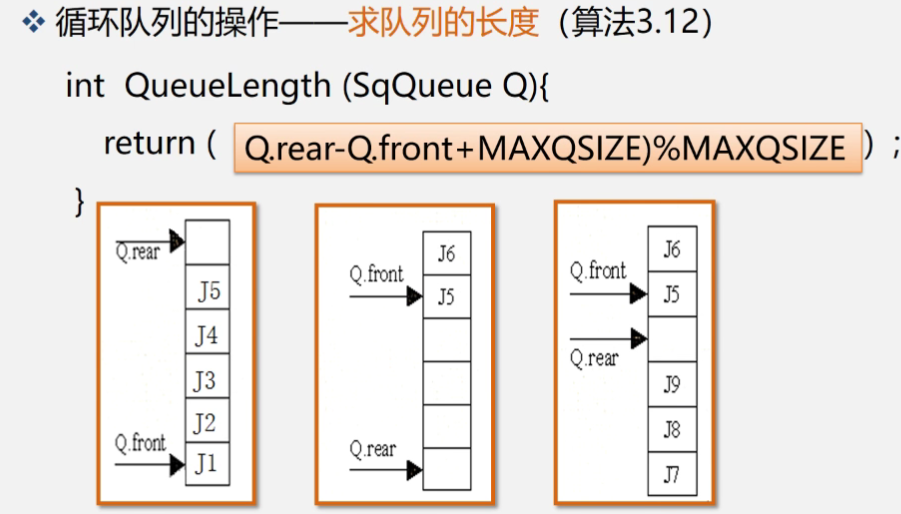
队列中f代表头,r代表尾,r代表的并不是最后一个元素,而是最后一个元素的下一个元素,例如图中的f到r,应该包含了三个元素,其中f指向的元素为第一个,编号为3和4的元素分别为第二个和第三个,r指向的为最后一个元素的下一个元素,所以其不算作元素。
当有人要出列时,我们需要做的是把f进行加操作,而不是减,原因是当我们对f进行减操作时,比如将f放到了1这个位置,那么不难发现元素竟然变多了,这明显不是我们所要的,所以我们需要进行的正是加操作。
当有人要入列时,我们需要对r进行加操作,原因同理,如果我们对r进行了减操作,那么元素数量反而变少了,这并不是我们想要的。
综上,也就是说无论我们进行何种操作,f和r都需要进行加操作,如果我们使用传统类型的数组来实现,r和f所卡住的元素个数会越来越少,最终会导致没卡住的元素越来越多,这些元素都无法再使用,导致了巨大的内存浪费。
当我们一直进行出对入队的操作时,总有一个时间会导致入队后rear指向的位置越出数组的界限,所以这时候传统的数组就不再合适了。我们需要循环数组。
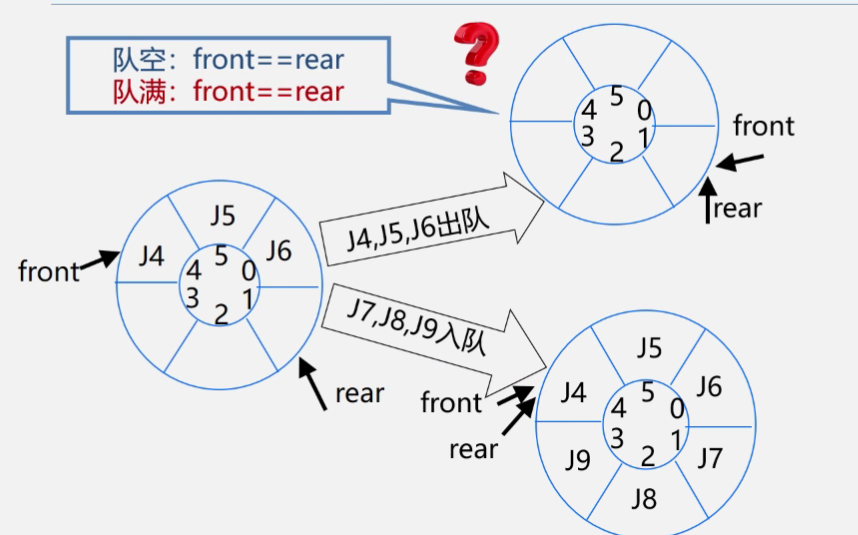
front为0时,这时rear指向了MAXQSIZE,前面的每个元素位置都有元素,所以无法再入队,这称之为真溢出
front不为0时,这是rear虽然指向了MAXQSIZE,但前面实际上是有空位的,所以这称之为假溢出
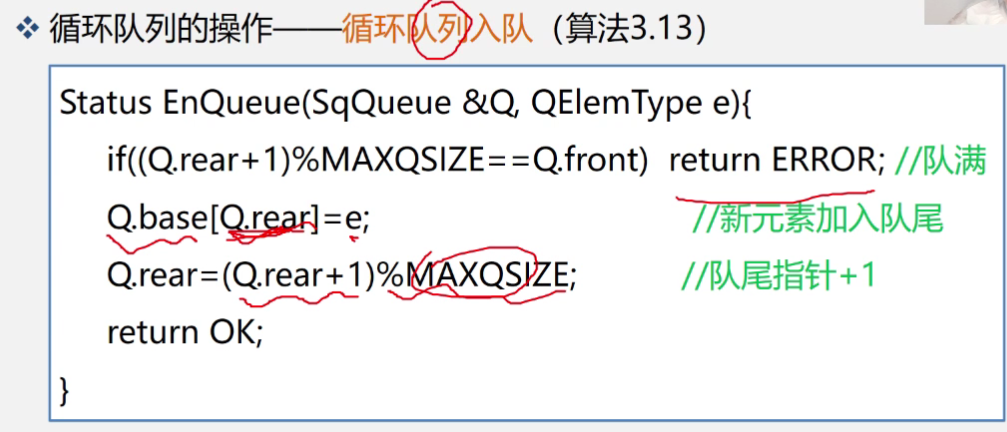
实现方法:
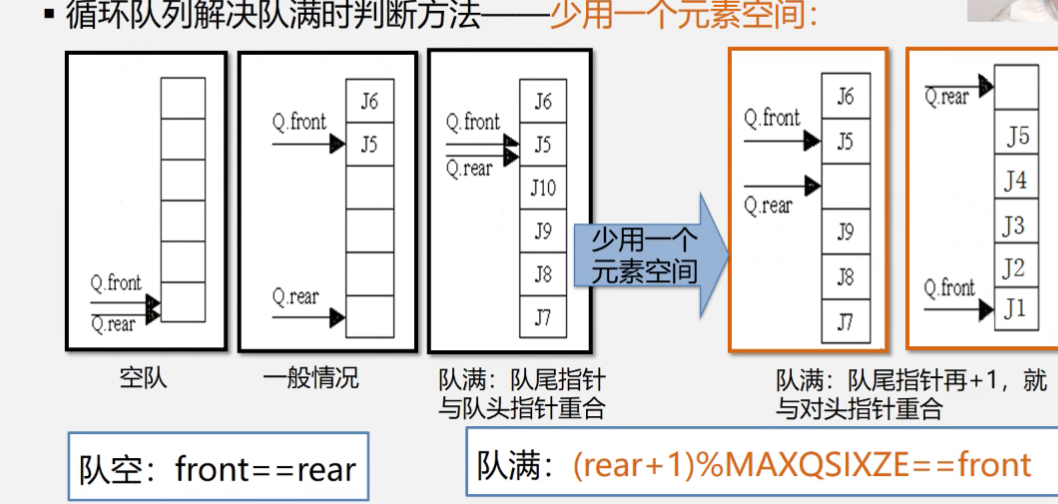
比如说现在的rear指针指向了1这个位置,我们如何判断是否需要将rear置回0呢,我们将现在的rear指向现在的下标加一与数组的长度进行取模运算,只要rear指向的不是数组的最后,那么结果一直都会是加一之后的数字,正好就是rear需要移至的位置,如果rear正好是数组的末尾,那么运算结果正好为0,回到了开始的地方。十分的巧妙
那么类比着,如果我们需要删除元素,队列需要在头部进行元素的删除,我们将要删除的元素赋值给一个变量,将front进行相同的操作来判断是否需要回到头部。
x=Q.base[s.front];
Q.front=(Q.front+1)%MAXQSIZE;
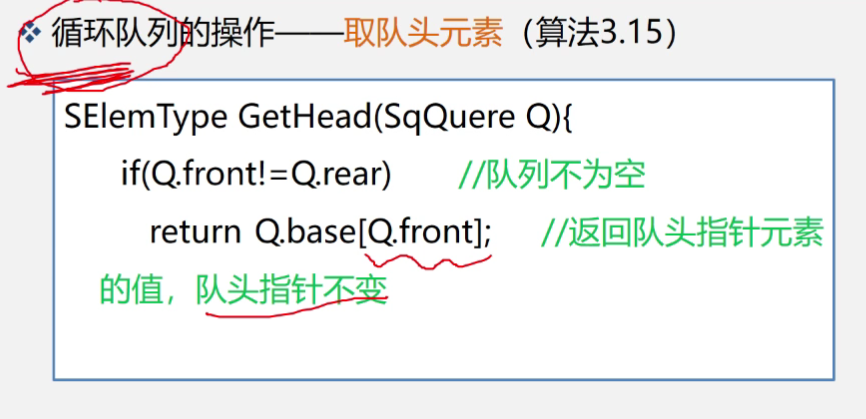
我们可以使用一个圈来理解循环队列,但要注意其实循环队列并不是真的一个环形。从图里不难发现,当队空和队满时,标志均为front和rear相等,我们需要找一个方法来将二者区分开来。
我们可以使用少用一个元素空间的方法来讲二者区分开来。
到此为止才真正明白,我们在删除一个元素时,和之前链表中的操作一样,我们利用一个变量来保存一下我们删除的元素,记录下来。
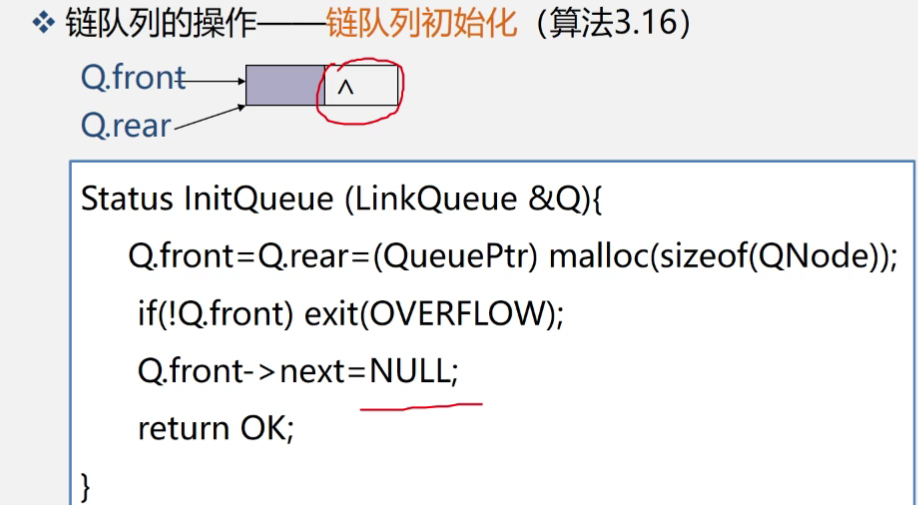
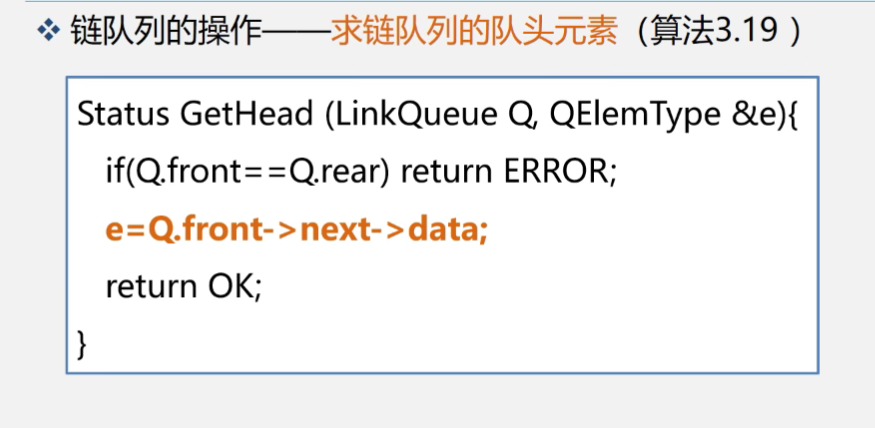
队列的链式表示与实现:
当用户无法估计所用队列的长度,则宜采用链队列
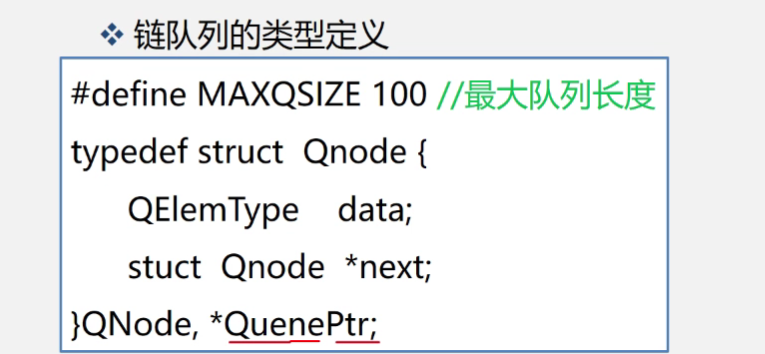
利用typedefine定义了一个数据类型,在数据类型的内部定义了一个指向自身数据类型的指针,即结点的指针域指向了一个和自己数据类型相同的结点next。QNode和Struct Qnode类型,代表着一个整的具体的大结点,包括指针域与数据域两部分,QueuePtr为struct Qnode*类型,代表着一个指向结点数据类型的指针。
再定义一个数据类型其中包括两个指针,在单链表中我们只用了一个指针,而在队列中我们需要两个指针,不妨放在了一起,规定这种数据类型为LinkeQueue
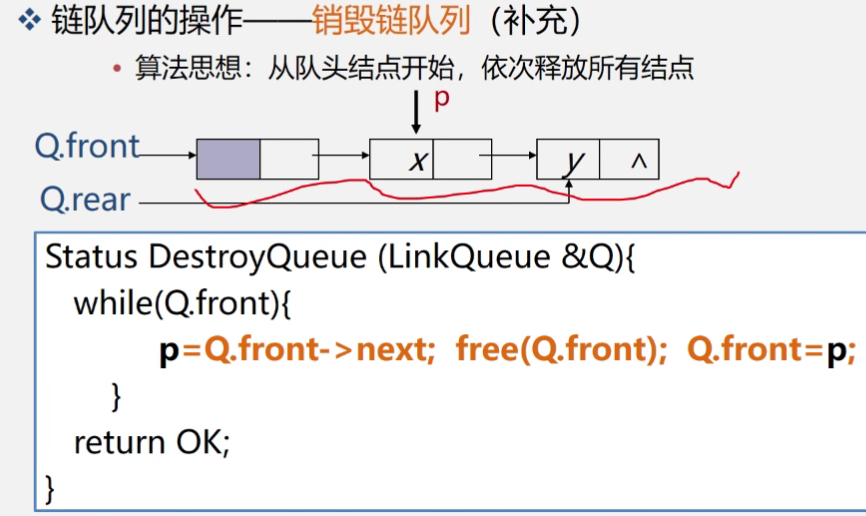
标为橙色的一行也可以利用Q.rear来写,利用空闲资源。Q.rear=Q.front->next;free(Q.front);Q.front=Q.rear;
首先创建一个新节点,然后将这个结点的数据域分配给用户输入的值,然后指针域指向为NULL,之后将原本的尾节点与这个新节点相接,最终再把新节点变为整个队列的尾即可
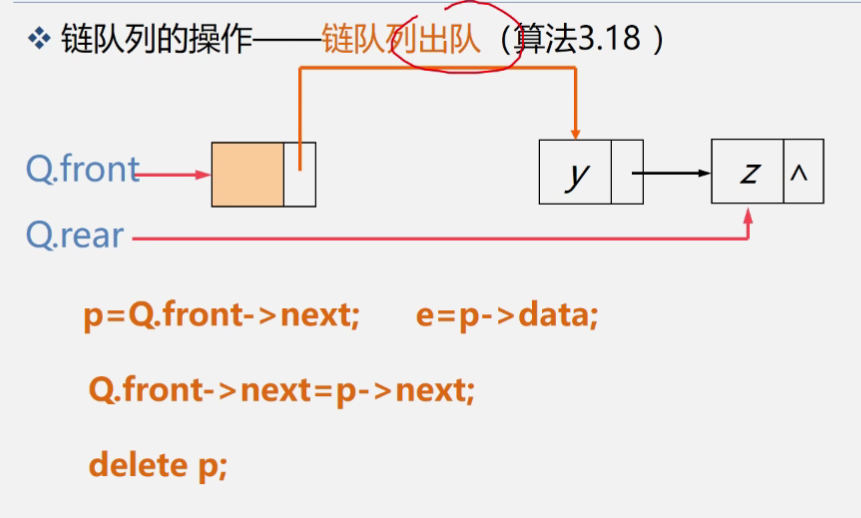
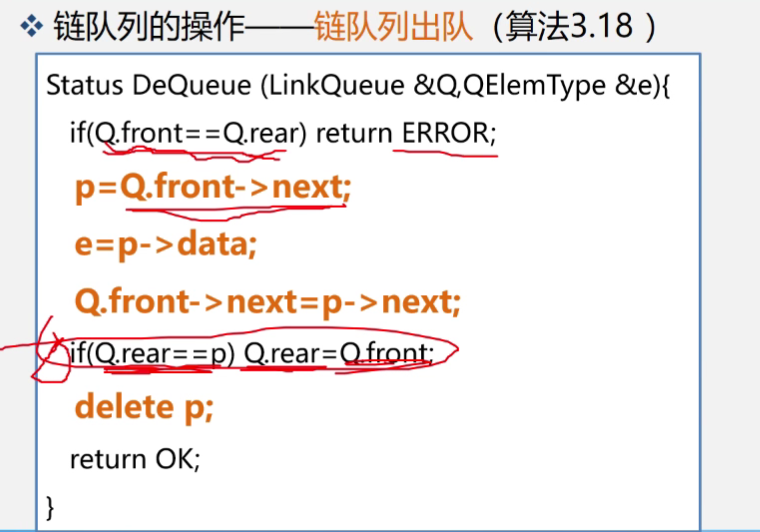
因为只能在队头进行出队,先将头结点的下一个结点中的数据保存,之后改变结点指向即可
需要注意的是,要出队一个结点时,p所指向的是头结点的下一个结点,如果这个节点正好是尾节点,那么它出队后,我们就不仅需要修改头结点,同时还要修改尾节点才可以。
3.串(内容受限的线性表)
串(String)是由零个或多个任意字符组成的有限序列
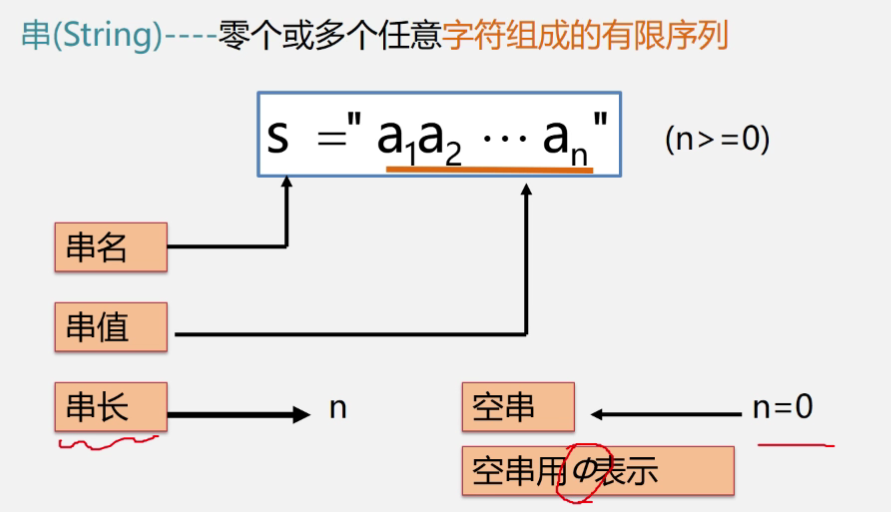

此处还有一个子序列的概念需和字串进行区分,子序列与字串的唯一区别就在于子序列不要求字符是连续的,而字串要求字符必须是连续的

当判断两个串是否相等时,只有两个串的长度与相对应位置的字符相同,才能说这两个串是相等的。
所有的空串都是相等的
串的顺序存储结构
#define MAXLEN 255
typedef struct{
char ch[MAXLEN+1];
int length;
}SString;
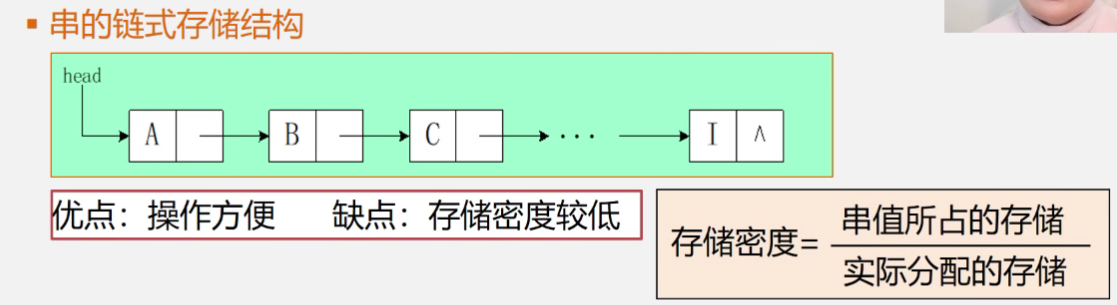
串的链式存储结构(块链结构)
关于如何计算存储密度:
单个节点中包括两部分内容,一个字符部分,一个指针部分,其中我们考虑字符为英文的情况下应占用一个字节,而指针会占用四个字节,所以一个节点总共会占用(4+1)=5个字节,所以存储密度即为存储的数据类型字符的字节数除以一个节点总共需要的字节数,结果为1/5=20%。由此可见这样存储会导致存储密度较低
那我们如何改进这个缺点呢,就是在一个节点中不只单单存入一个字符,而是存入许多字符,这样就可以使存储密度又高,操作又方便,并且随着存入的字符数量不断增加,存储密度也会不断增加
#define CHUNKSIZE 80 //块的大小可以自己定义
typedef struct Chunk{
char ch[CHUNKSIZE];
struct Chunk *next;
}Chunk;
typedef struct{
Chunk *head,*tail; //头指针和尾指针
int curlen; //当前长度
}LString; //字符串的块链结构
串的模式匹配算法:
算法种类:BF算法(Brute-Force,又称古典的、经典的、朴素的、穷举的)
KMP算法(速度快)
1.BF算法
算法目的:确定主串中所含字串(模式串)第一次出现的位置(定位)
算法应用:搜索引擎、拼写检查、语言翻译、数据压缩
首先S和T下标为0的位置均不存放字符,i和j分别都从1开始进行匹配,每次都将两个指针指向的字符进行匹配(这里的指针像是双指针中的指针,并不是真的指针变量),如果二者相同,则同时进一,如果发现二者无法匹配,则j返回到字串的头部位置,i从本次开始匹配的位置进一重新开始
如何理解i-j+2这一式子,我们可以将i和j均当作是向前移动的距离,例如j当前应该为4,但是其实是从1只向前移动了三格(j-1)步,所以说如果用i-j,就相当于多减了1,我们就要加回去,即(i-j+1),也就是代表将i回到移动之前指向的位置,又因为我们需要将i向前移动一格,所以要再加一,也就是最后的(i-j+2)
需要注意的是,当整个子串都被匹配完毕后,i和j并不是停在了最后一个字符的位置,而是要继续向后移动一个字符。我们依据当前的条件来判断是否匹配结束
最后一个问题是,我们如何求出这个字串是在主串的第几个位置出现的呢?答案是我们用当前的i值减去字串的长度即可,即$$i-length=3$$
实现:
//此为从头开始查找的BF算法
int Index_BF(SString S,SString T){
int i=1,j=1;
while(i<=S.length&&j<=T.length){
if(s.ch[i]==t.ch[j]){
i++;
j++;
}else{
i=i-j+2;
j=1;
}
}
if(j>=t.length) return i-t.length;
else return 0;
}
//此为从用户指定位置pos开始查找的BF算法
int Index_BF(SString S,SString T,int pos){
int i=pos,j=1;
while(i<=S.length&&j<=T.length){
if(s.ch[i]==t.ch[j]){i++;j++}
else {i=i-j+2}
}
if(j>=T.length) return i-T.length;
else return 0;
}
时间复杂度:
2.KMP算法
KMP(Kunth Morris Pratt)算法是由三位大佬共同提出的,KMP分别是这三位大佬名字的首字母
具体内容:
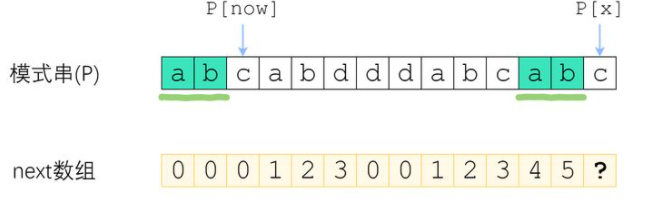
在了解KMP算法之前,我们先需要了解一个KMP算法中的精髓,即Next数组,值得一提的是,许多很强的算法都并不是上手就可以开始阅读的,可能都会存在一个新的概念在算法中,需要在已有的基础概念上多加理解(例如Timsort中的run数组)
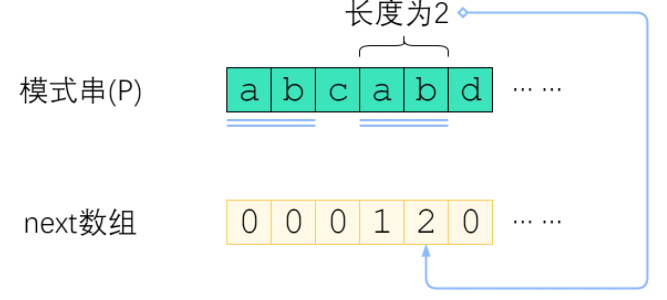
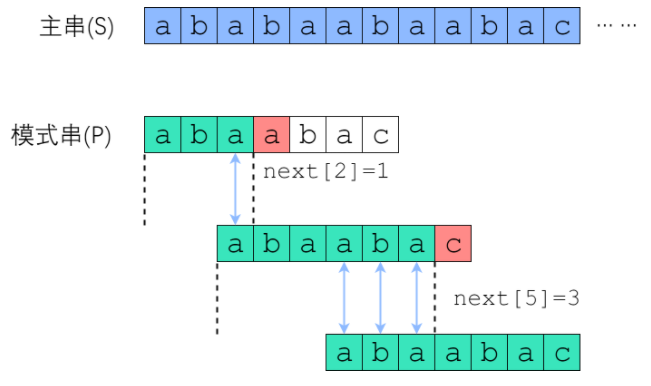
何为Next数组呢?P(模式串)的next数组定义为next[i]表示p[0]-p[i]这一个字串,使得前k个字符恰等于后k个字符的最大的k,特别地,k不能取i+1(因为这个字串一共才i+1个字符,自己肯定和自己相等,没有意义)
我们来举个例子:
在上图中的模式串P内,next[4]=2,也就是说P[0]到P[4]这个子串中,前2个和后2个字符是一样的,同理,next[5]=0
我们可以把模式串想象为是一把标尺,在主串上进行移动,暴力BF算法就是每次只移动一次,而KMP算法则是在此基础上进行改进,每次移动多次,跳过中间那些根本没有可能匹配成功的位置

那么我们是出于何种原因才想到要发明一个next数组的定义呢?
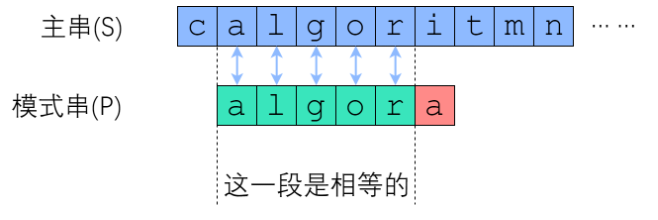
在使用BF算法时,我们不难发现,如果从主串S下标为i的字符开始匹配的一次失败了,那么BF算法会直接尝试从S[i+1]开始,这完全就是计算机思维——不会从错误中吸取任何经验与教训,人类其实很容易注意到,如果S[i:i+len(P)]与P的匹配是在第r个位置失败的,那么从S[i]开始的(r-1)个连续字符,一定与P的前(r-1)个字符一模一样
进一步深入,在匹配的过程中,有些字符串是有几率成功的,但有一些看都不用看肯定毫无任何希望,如果我们能让计算机识别出这些字符串直接跳过,那么就可以大大减少比较的趟数从而降低时间复杂度,那么问题是什么样的字符串毫无希望呢?
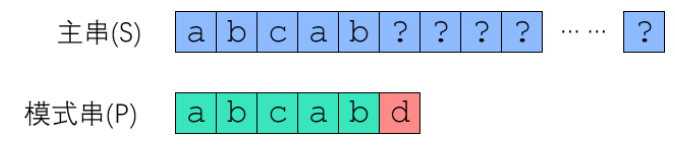
如上图所示,模式串P为abcabd,从S[0]开始匹配,在P[5]处失配,利用上文提到的思想,S[0:5]与P[0:5]肯定相同,那么我们来考虑一下,如果BF算法现在要从S[1]开始,你会同意吗?如果按照正常人的脑回路,是肯定不会同意的,因为S[1]位置的字符为b,第一个字符就已经与P[1]不同了,还有什么比较的意义呢?但是从S[3]开始的匹配是有可能成功的——至少我们现在觉得有可能成功(后面的?我们并不知道是什么)
于是乎,next数组就可以帮助我们干掉这些不可能成功匹配的字符串,这也就是KMP算法的精髓所在
但是一个新的问题又来了,我们现在知道要把模式串移动很多位的思想,那么到底要移动多少位呢?我们该如何确定呢?
如上图所示,在S[0]尝试匹配,失配于S[3]<=>P[3]之后,我们将模式串向右移动了两位,让S[3]对准了P[1]继续下一次匹配,失配于S[8]<=>P[6],我们将P向右移动了三位,把S[8]对准P[3]进行又一次匹配,直到成功为止
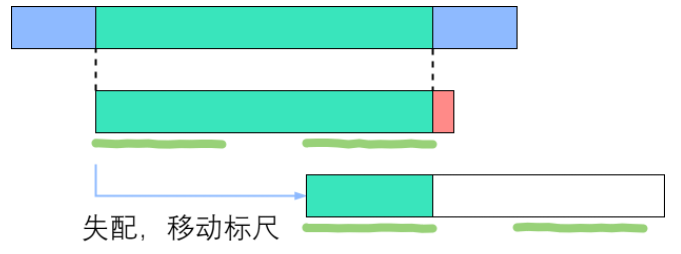
从图中可以很明显的看出,每次移动标尺后,旧的后缀与新的前缀一致
回忆next数组的性质:P[0]到P[i]这一段子串中,前next[i]个字符与后next[i]个字符一模一样。既然如此,如果失配在P[r],那么P[0]-P[r-1]这一段里面,前next[r-1]个字符恰好和后next[r-1]个字符相同——也就是说,我们可以用长度为next[r-1]的那一段前缀,来顶替当前后缀的位置,使得符合旧的后缀与新的前缀一致这个条件
我们可以用实际例子来验证一下加深理解,P[3]失配后,把P[next[3-1]]也就是P[1]对准主串失配的那一位即S[3];P[6]失配后,将P[next[6-1]]即P[3]对准失配的S[8]
绿色部分为成功匹配的部分,而红色部分为失配的部分。深绿色的下划线标出了相同的前缀和后缀,长度为next[右端],由于二者是相同的,我们直接将前半段下划线部分平移至于后半段下划线部分对其即可
到此为止我们已经可以用代码来实现这个非常惊叹的算法了,但是KMP算法真正的精髓还没有介绍,即快速求解Next数组
快速求解Next数组的核心思想是“模式串自己和自己进行匹配”
在next数组的定义中,包含这么一句“前缀和后缀相等”,这就是一次模式串自己和自己进行匹配的过程。我们考虑用递推来求出next数组。如果next[0]、next[1]……next[x-1]均已知,那么如何求出next[x]呢?
分类讨论一下,如果我们已经知道了next[x-1],如果P[x]和P[next[x-1]]相同,那么最长相等的前后缀只需要向后扩展一位即可,很明显next[x]=next[x-1]+1
可能还有些懵逼?我们再看一个实际的例子来加深理解:
假如我们现在有一个字符串是abbabb,当x=5时,不难得出上图所示的结论,我们可以发现P[next[x-1]]所对应的位置正好就是最长相等前缀的后一个位置,而P[x]所对应的位置正好就是最长相等后缀的后一个位置,如果这两个位置相等,那么理所应当的next数组的下一个值就是前一个值加一即可了
那么如果P[x]~=(!=)P[next[x-1]]呢?
我们利用一个数学里经常用的思想,试试能不能把一般情况转化为特殊情况,即让P[x]=P[next[x-1]]
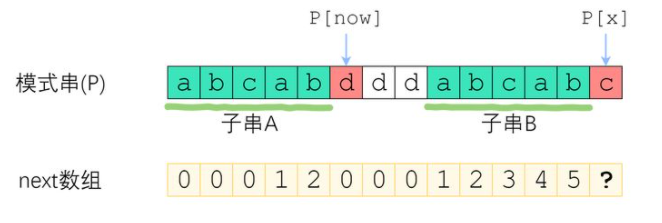
如上图所示。长度为now的字串A和B是P[0]-P[x-1]的最长公共前后缀。可惜A右边的字符和B右边的字符这时候不相等,next[x]不能改成next[x-1]+1了。因此,我们应该缩短这个now,来试试P[x]可不可以等于P[now]
我们应尽可能的让now不要太小,在达成目的前提下尽可能地让now大一点,因为这样掌握的已知信息就越多,效率就越高。也就是说要找到一个最大的k使得A的前k个字符等于B的后k个字符,且同时保证各自后一位相同
不难发现,串A与串B是相同的,即B的后缀与A的后缀是相同的,因此,串A的最长公共前后缀的长度next[now-1]其实就是最大的那个k,所以我们只需将now换为next[now-1]即可
至此,KMP算法真正的思想真正的结束了,KMP算法的时间复杂度为O(n+m),其中O(m)的时间用来构建next数组
KMP算法由Donald Knuth(K), James H. Morris(M), Vaughan Pratt(P)于1977年提出,感谢他们!
代码实现部分:
//快速求next数组
void get_nextval(SSting T,int &nextval[]){
i=1;nextval[1]=0;j=0;
while(i<T.length){
if(j==0||T.ch[i]==T.ch[j]){
++i;++j;
if(T.ch[i]!=T.ch[j]) nextval[i]=j;
else nextval[i]=nextval[j];
}
else j=nextval[j];
}
}
//KMP算法
int Index_KMP(SString S,SString T,int pos){
i=pos;j=1;
while(i<S.length&&j<T.length){
if(j==0||S.ch[i]==T.ch[j]){i++;j++}
else
j=next[j]; //i不变,j后退
}
if(j>T.length) return i-T.length; //匹配成功
else return 0; //返回不匹配标志
}
#Python3
s=input().strip()
p=input().strip()
nxt=[]
def buildNxt():
nxt.append(0)
x=1
now=0
while x<len(p):
if p[now]==p[x]:
now+=1
x+=1
nxt.append(now)
elif now:
now=nxt[now-1]
else:
nxt.append(0)
x+=1
def search():
tar=0
pos=0
while tar<len(s):
if s[tar]==p[pos]:
tar+=1
pos+=1
elif pos:
pos=nxt[pos-1]
else:
tar+=1
if pos==len(p):
print(tar-pos+1)
pos=nxt[pos-1]
buildNxt()
search()
print(' ',join(map(str,nxt)))
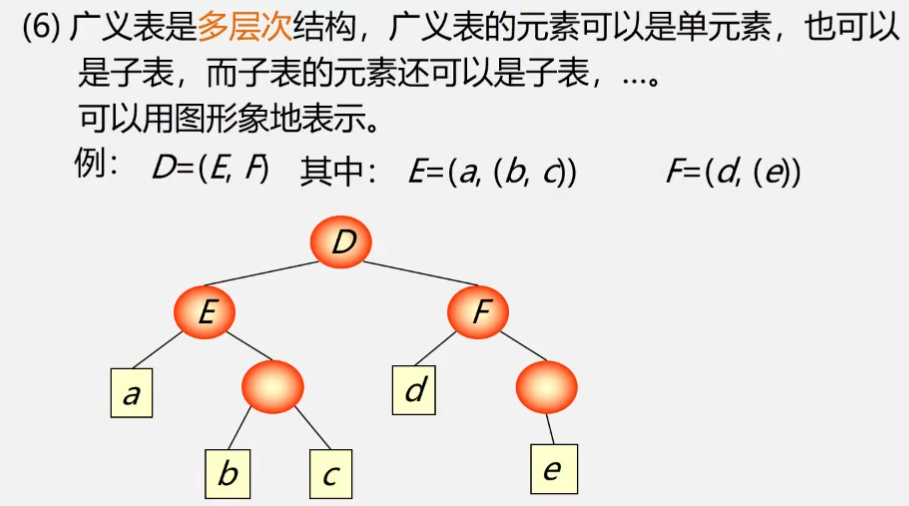
4.广义表
四.非线性结构
4.1树
树的定义
有且只有一个称为根的节点
有若干个互不相交的子树,这些子树本身也是一棵树
每个节点只有一个父节点,但可以有很多子节点;其中根节点没有父节点
深度:从根节点到最底层节点的层数
叶子节点:没有子节点的节点,根节点可以是叶子也可以是非叶子
非终端节点:实际就是非叶子节点
度:子节点的个数称为度
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径
路径长度:两个结点间线的数量
结点的权:每一个结点被赋予的一个数值
结点的带权路径长度:指的是从根节点到该结点之间的路径长度与该结点的权的乘积
树的分类
一般树:任意一个节点的子节点的个数都不受限制
二叉树:任意一个节点的子节点的个数最多为两个,且子节点的位置不可更改(有序树)
二叉树的分类:
满二叉树:在不增加树层数的前提下,无法再多添加一个节点的二叉树
完全二叉树:如果只是删除了满二叉树最底层最右边的连续若干个节点,这样形成的二叉树就是完全二叉树
满二叉树是完全二叉树的一个特例,正好是一个节点也不删除的完全二叉树
森林:n个互不相交的树的集合
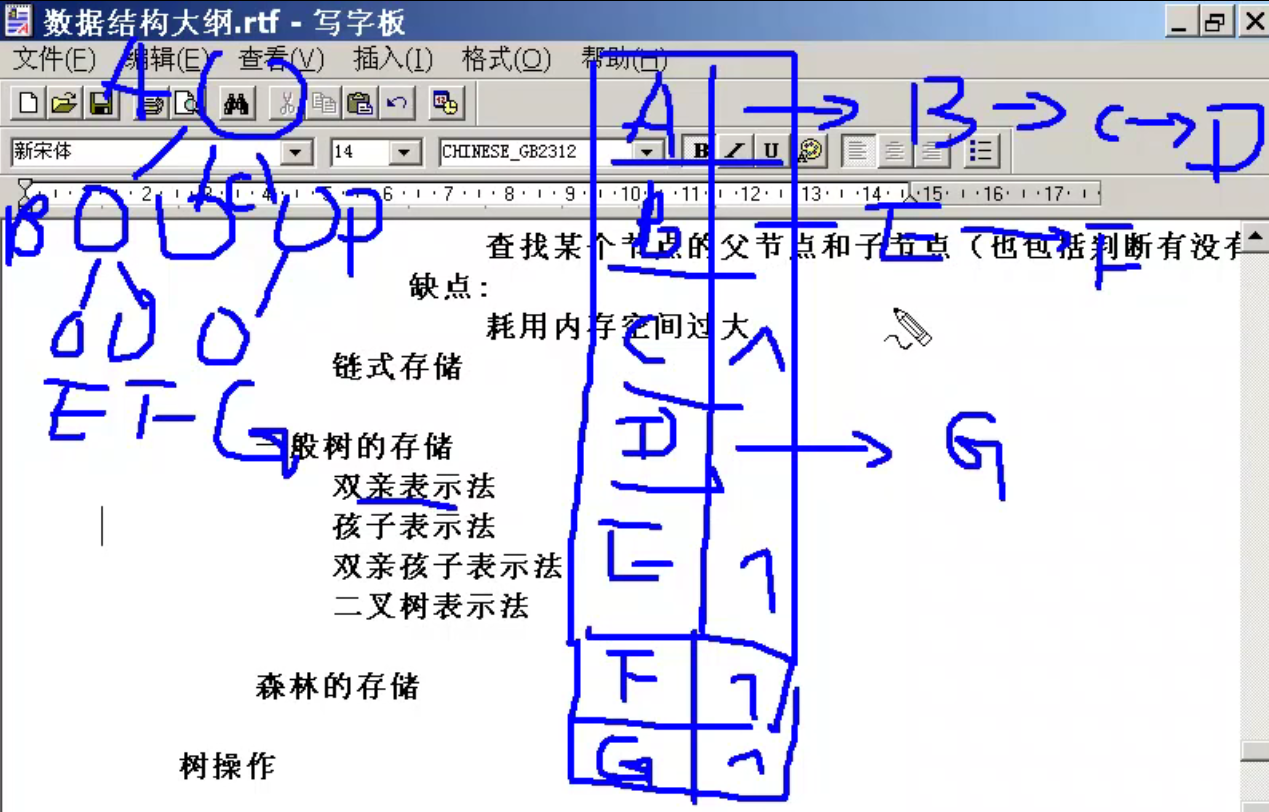
树的存储
二叉树的存储
连续存储[完全二叉树]:
如果我们要用数组这种线性的结构来存储树这种非线性的结构,就会导致无法分辨节点的先后顺序,造成混淆。所以在此之前,我们要先通过一个算法进行转换。
在转换之前,我们还需要将当前的树转换为完全二叉树才可以,原因有两点。
第一,树是一个非线性的结构,而内存是连续的,两者相矛盾,所以人们发明了先中后三种算法来进行二者的转换
第二,就算我们转换了之前的树,如果我们只转换了红色的有效节点,我们也不能通过转换后的结果反推出树的节点顺序,这就失去了转换的意义
如果我们转换为了完全二叉树,我们就可以通过当前节点的数量来判断出到了树的第几层,进而判断出节点的先后顺序
综上,我们需要先将树转换为完全二叉树才可以,这样会导致很消耗内存(添加了许多蓝色的垃圾节点),但好处是我们可以准确的知道一个结点的父节点和子节点等相关信息,同时也可以判断有没有子父节点
链式存储[]
一般树的存储:
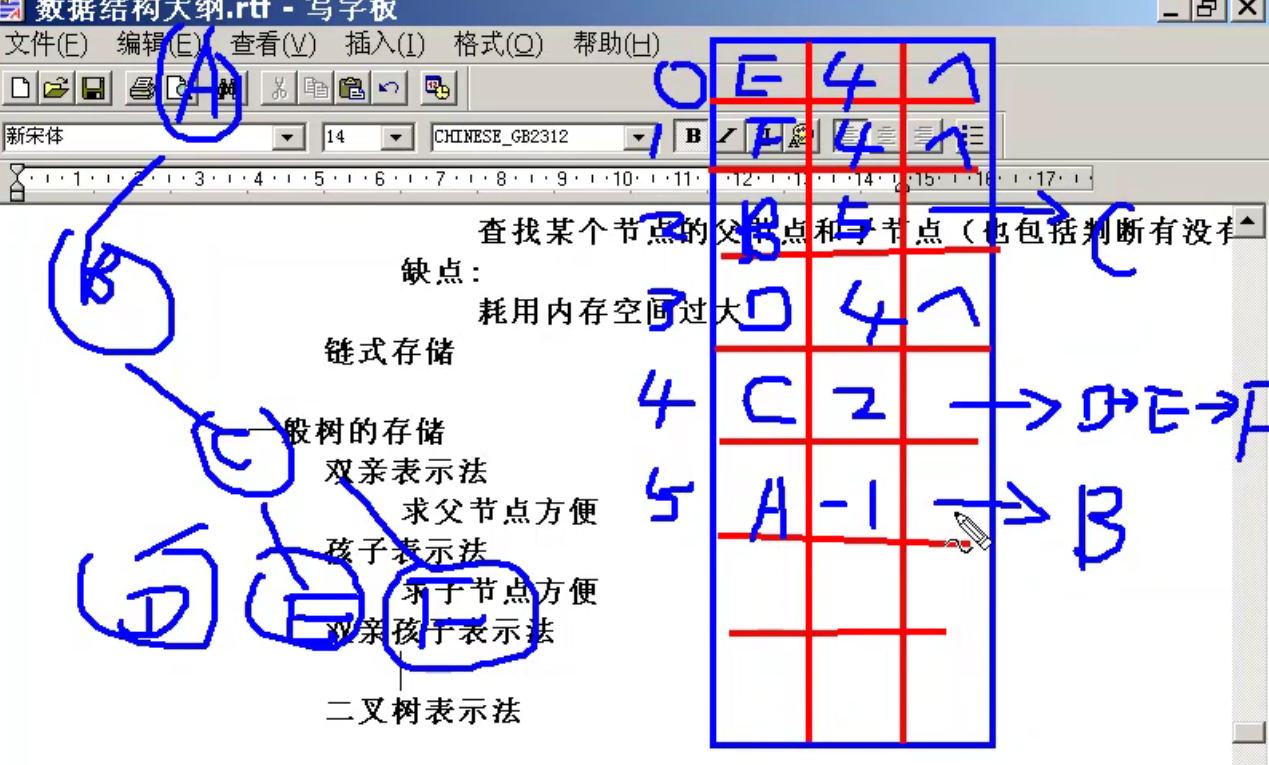
双亲表示法:
我们用一个数组来存储树中的节点与其对应的父节点,例如A节点为根节点,其无父节点,在数组中记为-1,接着B、C、D节点的父节点均为A节点,A节点对应的下标为0,于是0就存进B、C、D对应的位置,E节点的父节点为C,同理将C的下标4存入E对应的位置
双亲表示法求父节点十分的方便
孩子表示法顾名思义,就是存入节点对应的子节点,例如A节点的子节点为B、C、D,A对应的位置就存入B->C->D,以此类推,没有子节点的节点就存入null
孩子表示法对于求子节点十分的方便
为一个节点同时存储其父节点与子节点,也就是同时将双亲表示法与孩子表示法合在一起(想起了TimSort),例如E节点,其父节点为C,对应存储的数字为4,同时不存在子节点,于是便没有指向其他节点的存储
二叉树表示法:
虽然双亲孩子表示法已经很好了,但是对其操作时会非常的不方便,于是乎就有了二叉树表示法。
如何将一个普通树转换为二叉树来存储:
设法保证任意一个节点的左指针域指向它的第一个孩子,右指针域指向它的兄弟节点
一个普通树转换成的二叉树一定没有右子树
森林的存储:先把森林转换为二叉树,再存储二叉树(将不同的树之间的根节点当成兄弟节点)
二叉树操作:
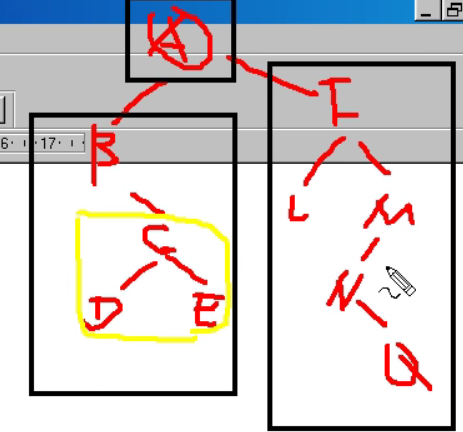
遍历
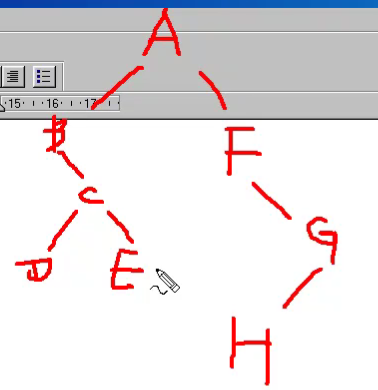
先序遍历[先访问根节点]:先访问根节点,再先序访问左子树,再先序访问右子树
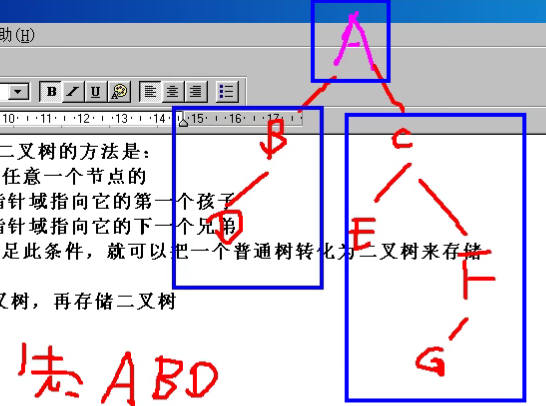
按照先访问根节点,再先序访问左子树,再先序访问右子树的方法来遍历上图所示的二叉树:
1.首先访问根节点A
2.访问A节点的左子树
3.将A节点的左子树也可以当作一个完整的新的二叉树,即根节点为B,对其进行访问
4.访问根节点B的左子树,也即节点D(又一棵新树的根节点)
5.访问D的左子树,此时发现D没有左子树,说明其左子树已经访问完毕
6.访问D的右子树,此时发现D没有右子树,说明D这个节点已经访问完毕
7.D已经访问完毕就代表B的左子树已经访问完毕,访问B的右子树
8.B没有右子树,代表B已经访问完毕
9.B和D都访问完毕,代表A的左子树已经访问完毕,此时访问A的右子树
10.同理,我们访问C节点,之后访问C节点的左子树即E节点
11.E节点均不存在左子树及右子树,所以我们回退访问C的右子树
12.C的右子树即为F节点,F节点访问完毕后,访问F的左子树即G节点
13.G节点不存在左子树右子树,访问完毕后回退F节点,访问其右子树
14.F不存在右子树, 至此访问完毕
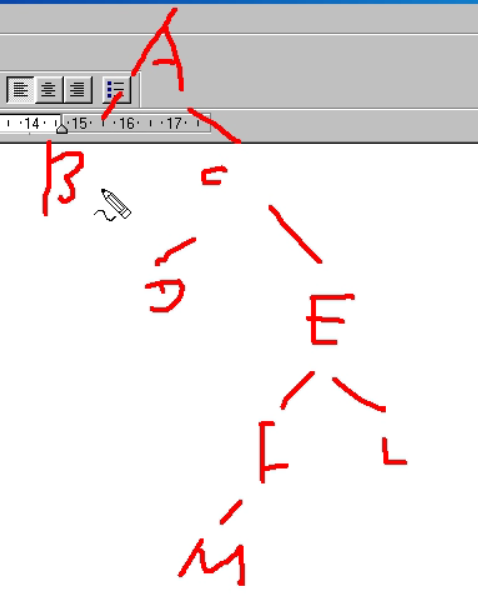
中序遍历[中间访问根节点]
中序遍历左子树,再访问根节点,再中序遍历右子树
1.首先我们中序遍历左子树,也就是左下角黑框框起来的位置
2.而左子树要中序遍历时,也就是要先中序遍历左子树的左子树,即B的左子树,但此时B没有左子树
3.所以我们访问根节点,即B节点
4.之后中序遍历右子树,即黄色框框起来的树
5.重复之前的步骤,先序遍历黄色框起来部分的左子树,也就是C的左子树,D这个节点
6.访问D的左子树,因为D没有左子树,所以回来访问D这个根节点
7.之后访问D的右子树进行中序遍历,没有右子树,此时黄色框的左子树遍历完毕
8.访问黄框树的根节点,即C节点,之后中序遍历其右子树,即E节点
9.同理,E没有左子树,回来访问根节点E,也没有右子树,至此黄框的树遍历完毕
10.B的右子树访问完毕,代表A的左子树访问完毕,返回访问根节点A
11.再中序遍历右子树,即右边的黑框框起来的部分
12.中序遍历右子树的左子树,即L节点,首先遍历L节点的左子树,但无左子树
13.返回访问根节点L,之后访问L节点的右子树,无右子树,此时右边黑框的左子树访问完毕
14.访问根节点F,之后中序遍历右子树
15.访问M节点的左子树,即N节点为根节点的新树
16.N节点无左子树,回来访问N节点本身,之后访问右子树,即Q为根节点的新树
17.Q节点无左子树,回来访问Q节点本身,之后访问Q节点的右子树,其无右子树,至此N的右子树访问完毕
18.N的右子树访问完毕代表M的左子树访问完毕,返回来访问根节点M,之后访问M的右子树
19.M无右子树,代表F的右子树访问完毕,至此代表A的右子树访问完毕。整棵二叉树访问完毕
后序遍历[最后访问根节点]
先中序遍历左子树,再中序遍历右子树,最后访问根节点
1.先中序遍历左子树,即以B为根节点的新树
2.以B为根节点的新树中无左子树与右子树,最后访问根节点即B
3.之后访问整棵二叉树的右子树,即以C为根节点的树
4.中序遍历左子树,即D,D无左右子树,返回访问节点D,此时C的左子树访问完毕
5.访问C的右子树,即E为根节点的新树
6.访问F节点的左子树M,M无左右子树,返回访问根节点M
7.F左子树访问完毕,且无右子树,返回访问根节点F
8.根节点F访问完毕后相当于E的左子树访问完毕,访问其右子树L
9.L无左右子树,返回访问其根节点L,至此E的左右子树访问完毕,返回访问根节点E
10.E节点访问完后,相当于C的左右子树均已访问完毕,访问根节点C
11.A节点左右子树均已访问完毕,访问根节点A。整棵二叉树访问完毕
已知两种遍历序列求原始二叉树
通过先序和中序或者中序和后序我们都可以还原出原始的二叉树,但是通过先序和后序是无法还原出原始的二叉树的
已知先序和中序(原理即为结合两种不同遍历方法的特性即可)
1.首先先序遍历会先访问整棵树的根节点,即A为整棵树的根节点
2.之后我们从中序中找到A,其左右两侧分别为A的左右子树
3.BDCE均位于A的左子树一侧,具体顺序需要通过先序判断,四者中先在先序出现的即为最早的根节点,上图先序中B最先出现,即B为左子树的根节点
4.因为B现在中序中出现,按照中序遍历的规则,其一定无左子树,否则B左侧还会有其他节点,于是DCE便为B的右子树部分,但具体位置也无法确定,所以同理利用先序进行判断
5.先序中DCE中最先出现的是C,所以右子树的最早的根节点为C,按照中序遍历的规则,C的左侧有一个D节点,说明C的左子树为D节点,之后返回到根节点C,再中序遍历右子树即图中的E节点
6.A的左子树求解完毕,右子树为FHG三个节点,通过先序判断前后顺序,最先出现的为F,即最早的根节点为F
7.因为F左侧没有节点,所以HG均为F的右子树部分,通过先序判断HG的先后顺序,先出现G,即G在H的前面
8.因为G左侧有一个H,说明H为G的左子树,先访问G的左子树H,之后返回到根节点G,最后遍历右子树,发现G无右子树,整棵二叉树还原完毕
已知中序和后序求先序
1.后序中最后的节点为根节点,即A为整棵树的根节点
2.之后将中序中的A左右分成两部分,即左侧为A的左子树,右侧为A的右子树部分
3.A的左子树中BDCE谁为根节点呢?即后序中最后出现的节点为根节点,于是得出B应为第一个根节点
4.由中序遍历的规则可知,B左侧没有节点即没有左子树,右侧DCE为其右子树,同理从后序中判断出C为接下来的根节点
5.C的左侧为D,即为C的左子树,右侧为E,即为C的右子树,至此A的左子树部分求解完毕
6.A的右子树部分为FHG,按照同样的方法从后序中找出最先出现的节点应为F
7.F的左侧没有节点,即没有左子树部分,右侧为HG,同理,找出G应为先出现的根节点
8.G左侧为H,即G的左子树部分为H,无右子树,至此整棵二叉树求解完毕
树的应用
树是数据库中数据组织的一种重要形式
操作系统子父进程的关系本身就是一棵树
面向对象语言中类的继承关系本身就是一棵树
哈夫曼树
链式二叉树的实现
#include "stdio.h"
#include "stdlib.h"
struct BinaryTreeNode{
char data;
struct BinaryTreeNode * pLchild;
struct BinaryTreeNode* pRchild;
};
struct BinaryTreeNode* createBinaryTree(){
struct BinaryTreeNode* pA=(struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* pB=(struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* pC=(struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* pD=(struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
struct BinaryTreeNode* pE=(struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));
pA->data='A';
pB->data='B';
pC->data='C';
pD->data='D';
pE->data='E';
pA->pLchild=pB;
pA->pRchild=pC;
pB->pRchild=pB->pLchild=NULL;
pC->pLchild=pD;
pC->pRchild=NULL;
pD->pLchild=NULL;
pD->pRchild=pE;
pE->pRchild=pE->pLchild=NULL;
return pA;
};
//先序遍历 先访问根节点 再访问左子树 最后访问右子树
//递归既浪费时间也浪费空间 所以要想着多做些特判
void PreTraverseBinaryTree(struct BinaryTreeNode * pT){
if(pT!=NULL){
printf("%c\n",pT->data);
if(pT->pLchild!=NULL){
PreTraverseBinaryTree(pT->pLchild);
}
if(pT->pRchild!=NULL){
PreTraverseBinaryTree(pT->pRchild);
}
}
}
//中序遍历
void InTraverseBinaryTree(struct BinaryTreeNode * pT){
if(pT->pLchild!=NULL){
InTraverseBinaryTree(pT->pLchild);
}
if(pT!=NULL){
printf("%c\n",pT->data);
if(pT->pRchild!=NULL){
InTraverseBinaryTree(pT->pRchild);
}
}
}
//后序遍历
void PostTraverseBinaryTree(struct BinaryTreeNode * pT){
if(pT->pLchild!=NULL){
PostTraverseBinaryTree(pT->pLchild);
}
if(pT->pRchild!=NULL){
PostTraverseBinaryTree(pT->pRchild);
}
if(pT!=NULL){
printf("%c\n",pT->data);
}
}
int main(){
struct BinaryTreeNode * pT=createBinaryTree();
// PreTraverseBinaryTree(pT);
// InTraverseBinaryTree(pT);
// PostTraverseBinaryTree(pT);
}
哈夫曼树
在开始哈夫曼树的学习之前,我们需要回顾一下关于树的概念
深度:从根节点到最底层节点的层数
叶子节点:没有子节点的节点,根节点可以是叶子也可以是非叶子
非终端节点:实际就是非叶子节点
度:子节点的个数称为度
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径
路径长度:两个结点间线的数量
结点的权:每一个结点被赋予的一个数值
结点的带权路径长度:指的是从根节点到该结点之间的路径长度与该结点的权的乘积
树的路径长度:从树根到每一个结点的路径长度之和
树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和
在结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树(不是充要条件,是充分条件)
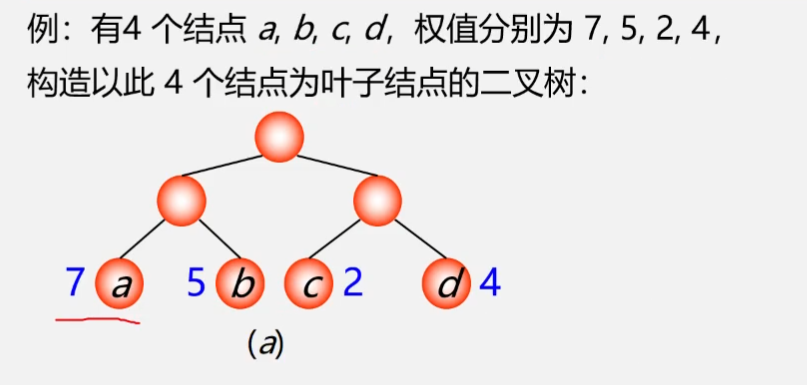
以上图为例,该树的带权路径长度为多少呢?
叶子节点为a、b、c、d,结点a的带权路径长度为$$2\times7=14$$,结点b的带权路径长度为$$2\times5=10$$,结点c的带权路径长度为$$2\times2=4$$,结点d的带权路径长度为$$2\times4=8$$,所以整棵树的带权路径长度为14+10+4+8=36
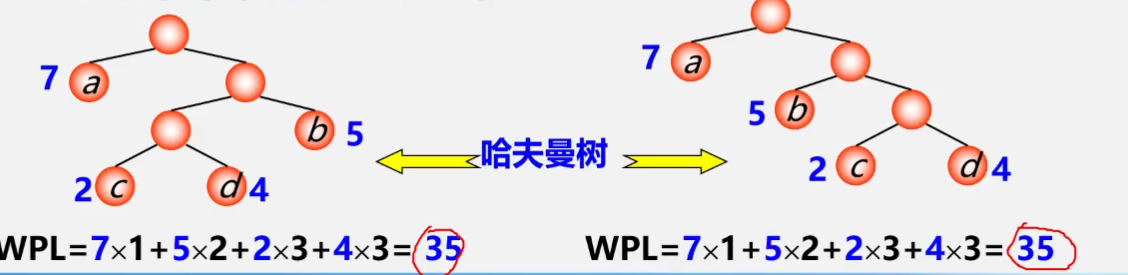
当叶子节点的个数相同且各节点对应的权值也相同时,并不代表构造出的树的带权路径长度就是唯一的,相反,实际上存在许多不同的情况,而哈夫曼树就应运而生
哈夫曼树也可以叫最优树,即带权路径长度(WPL)最短的树。这里的“带权路径长度”是在“度相同”的树中比较而得的结果,因此有最优二叉树、最优三叉树之称等
我们只讨论最优二叉树,接下来所说的哈夫曼树均指最优二叉树
上图即为例子的哈夫曼树,不难发现,满二叉树不一定是哈夫曼树,哈夫曼树中权越大的叶子离根越近,具有相同带权结点的哈夫曼树不唯一
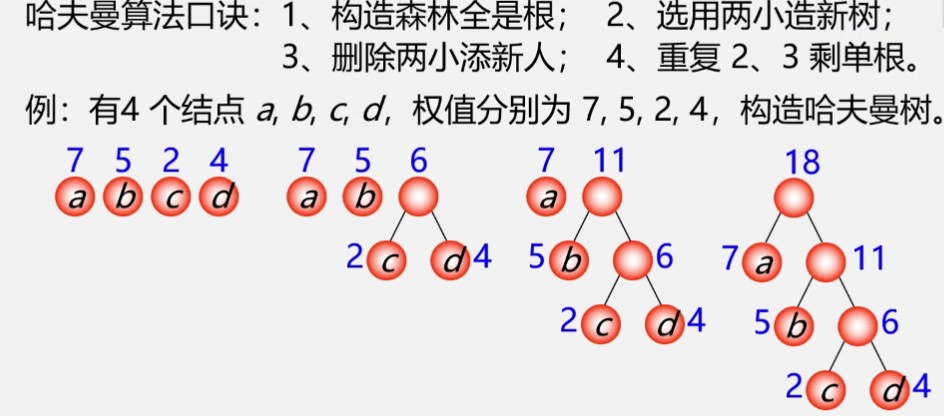
在哈夫曼树中,结点的度数均为0或2,没有度为1的结点;包含n个叶子结点的哈夫曼树中共有2n-1个结点;在哈夫曼算法中,初始有n棵二叉树,要经过n-1次合并最终形成哈夫曼树;经过n-1次合并产生n-1个新结点,且这n-1个新结点都是具有两个孩子的分支结点
代码实现:
//首先初始化 即将所有结点当作根节点构造森林 并且将双亲与左孩子右孩子都设置为0
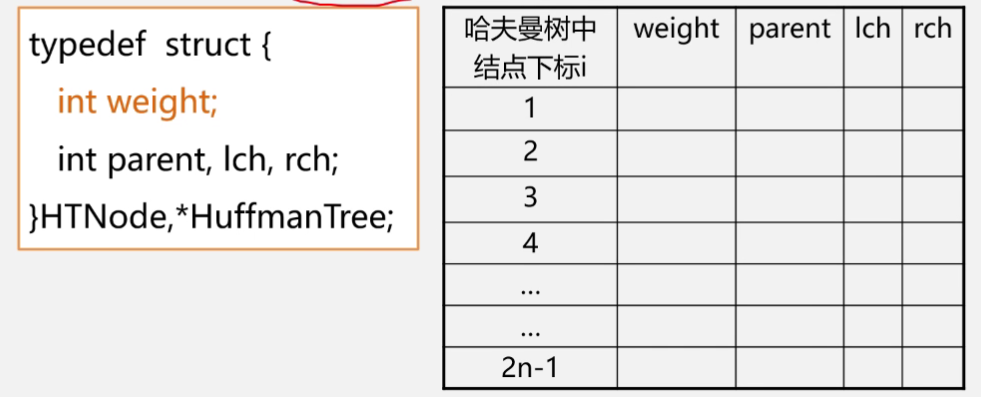
typedef struct{
int weight;
int parent,lch,rch;
}HTNode,*HuffmanTree;
void Select(HuffmanTree &H,const int n,int &i1,int &i2){
vector<int> vec;
for(int i=1;i<=n;++i){
if(H[i].parent==0){
vec.push_back(i);
}
}
auto flag1=vec.begin();
for(auto it=vec.begin()+1;it!=vec.end();++it){
if(H[*it].weight<H[*flag1].weight){
flag1=it;
}
}
i1=*flag1;
vec.erase(flag1);
auto flag2=vec.begin();
for(auto it=vec.begin()+1;it!=vec.end();++it){
if(H[*it].weight<H[*flag2].weight){
flag2=it;
}
}
i2=*flag2;
}
void CreatHuffmanTree(HuffmanTree HT,int n){
if(n<=1) return;
m=2*n-1; //我们一共需要2n-1个结点
HT=new HTNode[m+1]; //下标为0的位置我们不存放数据 从1-2n-1存放
for(i=1;i<=m;++i){ //初始化 置零
HT[i].lch=0;
HT[i].rch=0;
HT[i].parent=0;
}
for(i=1;i<=n;++i) cin>>HT[i].weight; //输入前n个元素的权值
//开始构造哈夫曼树
for(i=n+1;i<=m;i++){
Select(HT,i-1,s1,s2) //在已有的结点中找出最小的和次小的两个结点,返回他们的下标
HT[s1].parent=i;//Select算法中我们只在双亲为0的结点中进行选择,所以此步等于删除这两个结点
HT[s2].parent=i;
HT[i].lch=s1;//设置左右孩子
HT[i].rch=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;//权值求和
}
}
哈夫曼编码
哈夫曼编码是一种使电文总长最短的前缀码
性质:哈夫曼编码是前缀码且是最优前缀码
代码实现:
//从叶子到根逆向求每个字符的哈夫曼编码,存储在编码表HC中
void CreatHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n){
/*HC是一个字符指针数组 每一个单元内都存放了一个指向一个字符数组的指针
*/
HC=new char *[n+1];
cd=new char [n]; //分配临时存放编码的动态数组空间
cd[n-1]='\0'; //编码结束符
for(i=1;i<=n;++i){ //逐个字符求哈夫曼编码
start=n-1;c=i;f=HT[i].parent;
while(f!=0){ //从叶子结点开始向上回溯,直到根结点
--start; //回溯一次start向前指一个位置
if(HT[f].lchild==c) cd[start]='0'; //结点c是f的左孩子,则加入0
else cd[start]='1'; //结点c是f的右孩子 则加入1
c=f;f=HT[f].parent; //继续向上回溯
}
HC[i]=new char [n-start]; //为第i个字符串编码分配空间
strcpy(HC[i],&cd[start]); //将求得的哈夫曼编码复制到HC当前行
}
delete cd; //释放临时空间
}
文件的编码与译码
4.2图
标签:左子,结点,struct,int,笔记,学习,数据结构,节点,指针 来源: https://www.cnblogs.com/appletree24/p/16484130.html