统计基础篇之十二：怎么理解正态分布(一)

引用：https://zhuanlan.zhihu.com/p/24732117

一般正态分布的概率密度函数为：

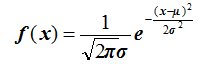
其中：μ、σ分别为均值和标准差

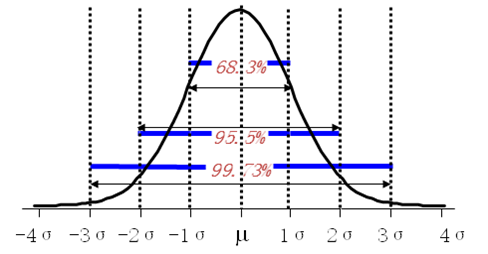
正态分布中，±1σ、±2σ、±3σ下的概率分别是68.3%、95.5%、99.73%，这3个数最好记住。

均值决定曲线的位置，标准差决定曲线的胖瘦。可以比较以下几种情况来理解正态分布。

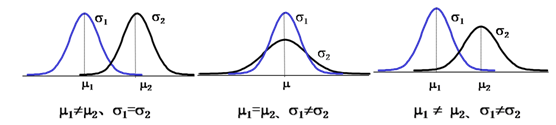
正态分布在实践中成功地被广泛应用，主要是因为正态分布在数学方面具有多种稳定性质，这些性质包括：

1.两个正态分布密度的乘积还是正态分布

2.两个正态分布密度的卷积还是正态分布，也就是两个正态分布的和还是正态分布

3.正态分布N(0，σ^2)的傅里叶变换还是正态分布

4.中心极限定理保证了多个随机变量的求和效应将导致正态分布

5.正态分布和其它分布具有相同方差的概率分布相比，具有最大熵

前上性质说明了正态分布一旦形成，就容易保持该形态的稳定。后两个性质则说你们，其它的概率分布在各种操作之下容易越来越靠近正态分布。

正是由于正态分布多种的稳定性质，使得它像一个黑洞一样处于一个中心的位置，其它概率分布形式在各种操作之下都逐渐向正态分布靠拢。

标签：其它,概率分布,均值,十二,理解,标准差,正态分布,性质
来源： https://www.cnblogs.com/bruce1992/p/16483632.html