教辅的组成

题目传送门 洛谷P1231 教辅的组成

题目背景

滚粗了的 HansBug 在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻 HansBug 在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而 HansBug 还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug 想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入格式

第一行包含三个正整数 \(N_1\)、\(N_2\)、\(N_3\)，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数 \(M_1\)，表示书和练习册可能的对应关系个数。

接下来 \(M_1\) 行每行包含两个正整数 \(x\)、\(y\)，表示第 \(x\) 本书和第 \(y\) 本练习册可能对应。（\(1\)\(\leq\)\(x\)\(\leq\)\(N_1\)，\(1\)\(\leq\)\(y\)\(\leq\)\(N_2\)）

第 \(M_{1+3}\) 行包含一个正整数 \(M_2\)，表述书和答案可能的对应关系个数。

接下来 \(M_2\) 行每行包含两个正整数 \(x\)、\(y\)，表示第 \(x\) 本书和第 \(y\) 本答案可能对应。（\(1\)\(\leq\)\(x\)\(\leq\)\(N_1\)，\(1\)\(\leq\)\(y\)\(\leq\)\(N_3\)）

输出格式

输出包含一个正整数，表示最多可能组成完整书册的数目。

样例 #1

样例输入 #1

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

样例输出 #1

2

提示

样例说明：

如题，\(N_1=5\)，\(N_2=3\)，\(N_3=4\)，表示书有 \(5\) 本、练习册有 \(3\) 本、答案有 \(4\) 本。

\(M_1=5\)，表示书和练习册共有 \(5\) 个可能的对应关系，分别为：书 4 和练习册 3、书 2 和练习册 2、书 5 和练习册 2、书 5 和练习册 1 以及书 5 和练习册 3。

\(M_2=5\)，表示数和答案共有 \(5\) 个可能的对应关系，分别为：书 1 和答案 3、书 3 和答案 1、书 2 和答案 2、书 3 和答案 3 以及书 4 和答案 3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书 2 + 练习册 2 + 答案 2、书 4 + 练习册 3 + 答案 3。

数据规模：

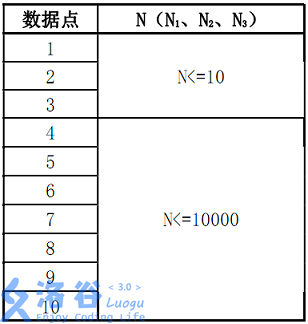
对于数据点 \(1\), \(2\), \(3\)，\(M_1\), \(M_2\leq 20\)

对于数据点 \(4-10\)，\(M_1\), \(M_2 \leq 20000\)

思路

题目最多蓝题难度没到紫题水平感觉

拆个点就行了..

blabla..

代码实现

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=1e6,M=200100,inf=1e8;
int is[N];

struct node
{
	int st,ed;
}edge[520];
	int tt,S,T,n,m,k;
    int e[M],ne[M],f[M];
    int q[N],cur[N],h[N],d[N],idx;
    
   int point[1010];
    
void add(int a,int b,int c)
{
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}
void add_(int a,int b,int c)
{
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;

}
inline bool bfs()
	{
		int tt=0,hh=0;
		memset(d,-1,sizeof d);
		q[0]=S,d[S]=0,cur[S]=h[S];
		
		while(hh<=tt)
		{
			int t=q[hh++];
			for(int i=h[t];~i;i=ne[i])
			{
				int ver=e[i];
				if(d[ver]==-1&&f[i])
				{
					d[ver]=d[t]+1;
					cur[ver]=h[ver];
					if(ver==T) return true;
					q[++tt]=ver;
				}
			}
		}
		return false;
	}	
 int find(int u,int limit)
	{
		if(u==T) return limit;
		int flow=0;
		
		for(int i=cur[u];~i&&flow<limit;i=ne[i])
		{
			int ver=e[i];
			cur[u]=i;
			if(d[ver]==d[u]+1&&f[i])
			{
				int t=find(ver,min(limit-flow,f[i]));
				if(!t) d[ver]=-1;
				f[i]-=t;
				f[i^1]+=t;
				flow+=t;	
			}
			
		}
		return flow;
	}
	
int dinic()
{
	int ans=0,flow;
	while(bfs())
	{
		while(flow=find(S,inf)) ans+=flow;
	}
	return ans;
}




int main()
{
	cin>>n>>m>>k;
	S=0,T=n+m+n+k+2;
	memset(h,-1,sizeof h);
	int q,qq;
	cin>>q;
	for(int i=1;i<=q;i++)
	{
		int u,v;
		cin>>v>>u;
		add(u,v+m,1);//练习册和书
	}
	cin>>qq;
	for(int i=1;i<=qq;i++)
	{
		int u,v;
		cin>>u>>v;
		add(u+m+n,n+n+m+v,1);//书和答案
	}
	for(int i=1;i<=n;i++)
	{
		add(i+m,i+n+m,1);
	}
    for(int i=1;i<=m;i++) add(S,i,1);
    for(int i=1;i<=k;i++) add(i+m+n+n,T,1);
	cout<<dinic();
	return 0;
}                

标签：正整数,idx,int,题解,教辅,leq,练习册,答案,组成
来源： https://www.cnblogs.com/watasky/p/16483520.html