1
作者:互联网
无损加密
题目描述
\(n\times m\) 的矩形,进行 \(q\) 次变换,设 \(k\) 次变换后的矩阵是 \(A_k\),初始 \(A_0\) 是单位矩阵。每次变换给定 \((l_k,r_k,c_k,d_k)\):
\[(A_k)_{ij}=\begin{cases}d_k(A_{k-1})_{ij} & j\not\in [l_k,r_k]\\d_k\sum_{t=l_k}^j(c_k)^{j-t}(A_{k-1})_{it} & j\in[l_k,r_k]\\\end{cases} \]求 \(f(A_q)\),其中 \(f(B)\) 定义为:
\[f(B)=\Big(\sum_{S\subseteq\{1,2...m\},|S|=n}\det B_{S}\Big)\bmod (10^9+7) \]其中 \(B_S\) 表示矩阵 \(B\) 的所有行与 \(S\) 中元素对应的列,交叉处生成的一个 \(n\times |S|\) 的矩阵。
数据范围保证对于所有的 \(1\leq i\leq m\),都有:
\[\sum_{i=1}^q[i\in[l_k,r_k]]\leq s \]\(2\leq n\leq m\leq 2\cdot 10^5,1\leq s\leq 8,q\leq sm\)
解法
真理:永远不要丝门弄数。
这题没有什么好的突破口,考虑从答案的角度入手,我们如何理解答案中出现的行列式?
谈到行列式,丝告诉我们,常见的模型有:\(\tt Binet-Cauthy\) 公式、矩阵树定理、\(\tt LGV\) 引理。最和本题贴合的是 \(\tt LGV\) 引理,我们把矩阵理解成 \(\tt LGV\) 引理中两点间路径的方案数,考虑构造一张分层图:
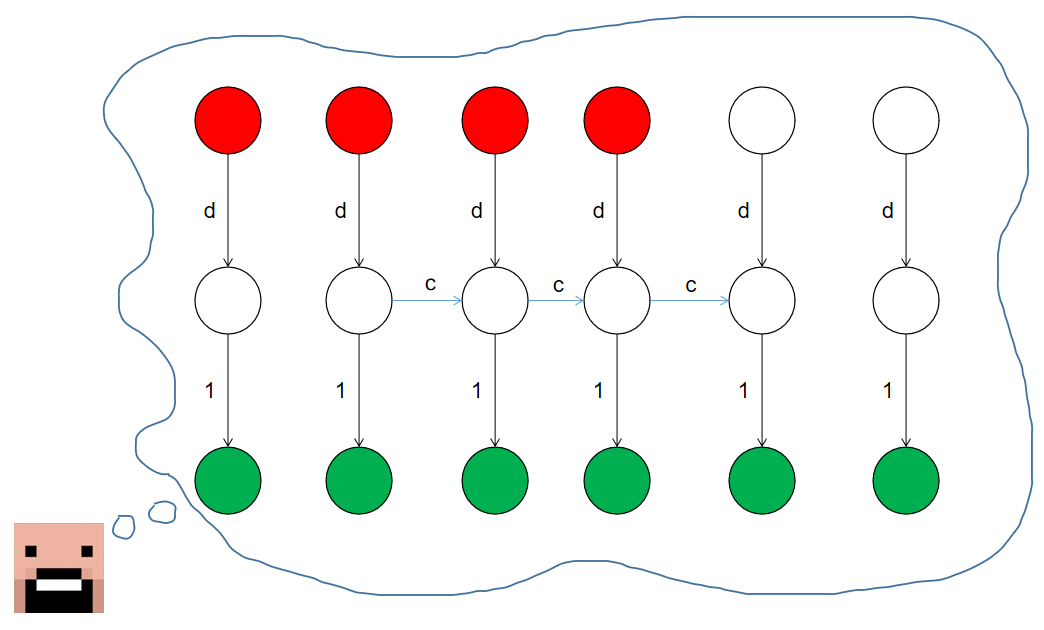
解释一下上面的构造:第一层有 \(n\) 个红点代表起点;最后一层有 \(m\) 个绿点代表终点。根据 \(\tt LGV\) 引理,我们只需要求出 \(n\) 条点不相交的路径,从红点开始在绿点结束的方案数。路径的权值是边权的乘积,方案的权值是路径权值的乘积。
再解释一下 \(B_S\) 这个东西,这对应了方案中的任意选择终点,所以被考虑进去了。
每一次变换相当于添加了 \(m\) 个点,和上一层的对应点连一条边权为 \(d\) 的边。对于在 \([l_i,r_i)\) 中的点,和下一个点连一条边权为 \(c\) 的边,这样构造正好能对应变换规则。
那么问题转化成在上图中求 \(n\) 条不交路径的方案数,直接 \(dp\) 很困难。
利用题目中 \(s\) 的条件,考虑切换 \(dp\) 主体,即我们不再按行 \(dp\) 而是按列 \(dp\)。那么每一列最多存在 \(9\) 个路径暂时的终点,可以暴力状压下来,设 \(dp[i][s]\) 表示考虑到第 \(i\) 列,集合 \(s\) 中的点作为终点的方案数(全集是这一列所有存在入边的点)
一个暴力的转移方法是,我们枚举这一层每个点对应走到下一层的哪个点,由于不交的限制,复杂度大概是 \(O(q\cdot 2^{2s})\)
再深入的分析,其实每个点都对应着下一层的一个范围,这个范围中的点是只有这个点能走到的。所以可以先传递给下一层离得最近的一个点,再考虑到下一层的时候考虑层间的转移,复杂度大概是 \(O(q\cdot 2^{s})\)
对于前 \(i\leq n\) 列,转移时需要加入起点;如果终点在 \(s\) 中,转移到下一层时需要把终点删除(代表这条路径结束)
还是不太好讲清楚,可以结合代码理解具体怎么 \(dp\) 的。
真理:永远不要丝门弄数。
总结
这种逆向思考的题目通常是难以下手的,但是出题人造出这道题一定是正向出发的。
所以正确的打开方式是,抓住题目中有特征的关键东西,然后考虑和这东西有关的理论,尝试套用一些经典模型。
#pragma GCC optimize("Ofast")
#pragma GCC target("avx", "sse")
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 200005;
#define int long long
#define pb push_back
#define z(x) (1<<(x))
const int MOD = 1e9+7;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,po,dp[2][1<<9];vector<int> v[M],W[M];
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
void add(int &x,int y) {x=(x+y)%MOD;}
signed main()
{
freopen("encode.in","r",stdin);
freopen("encode.out","w",stdout);
n=read();m=read();k=read();po=1;
for(int cnt=0;k--;)
{
int l=read(),r=read(),c=read(),h=read();
po=po*h%MOD;
for(int i=l;i<r;i++)
v[i].pb(++cnt),W[i].pb(c);
}
dp[0][0]=1;
for(int t=1,w=0;t<=m+1;t++,w^=1)
{
memset(dp[w^1],0,sizeof dp[w^1]);
static int a[11]={},b[11]={},d[11]={};
int n1=0,n2=0;
for(auto x:v[t-1]) a[n1++]=x;
for(auto x:v[t]) b[n2++]=x;
for(int i=0,k=0;i<n1;i++)
{
while(k<n2 && b[k]<a[i]) k++;
d[i]=k;
}
//down
for(int i=0;i<n1;i++)
for(int s=0;s<z(n1+1);s++)
if((s>>i&1) && !(s>>(i+1)&1))
add(dp[w][s^z(i)^z(i+1)],dp[w][s]);
//delete the last one
for(int s=0;s<z(n1);s++)
add(dp[w][s],dp[w][s|z(n1)]);
if(t>m) break;
//to next
for(int s=0;s<z(n1);s++) if(dp[w][s])
{
int ts=0,c=0,x=dp[w][s];
if(t<=n) ts=1,c++;
for(int i=0;i<n1;i++) if(s>>i&1)
ts|=z(d[i]),c++,x=x*W[t-1][i]%MOD;
if(__builtin_popcount(ts)!=c) continue;
add(dp[w^1][ts],x);
}
}
printf("%lld\n",dp[m&1][0]*qkpow(po,n)%MOD);
}
标签:,leq,int,tt,read,dp,MOD 来源: https://www.cnblogs.com/C202044zxy/p/16463153.html