Kruskal 重构树
作者:互联网
\(Kruskal\) 重构树
如何构造
先把边从小到大排序
在 \(Kruskal\) 合并两个点 \(a,b\) 所在的集合时,新建一个节点 \(x\) 同时连接 \(a,b\),且 \(x\) 的点权等于 \(a,b\) 之间的边权
如这样一个图
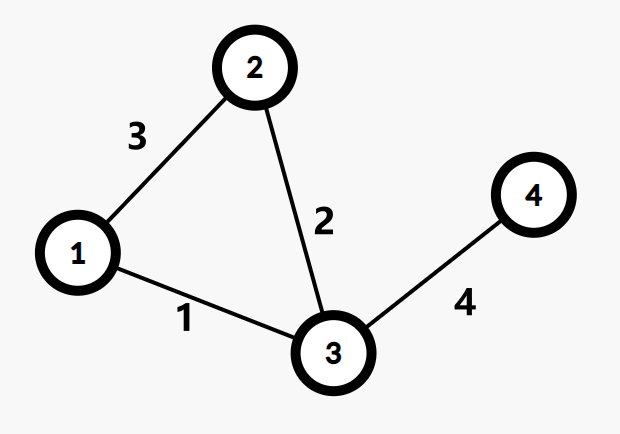
我们先把边权从小到大排序
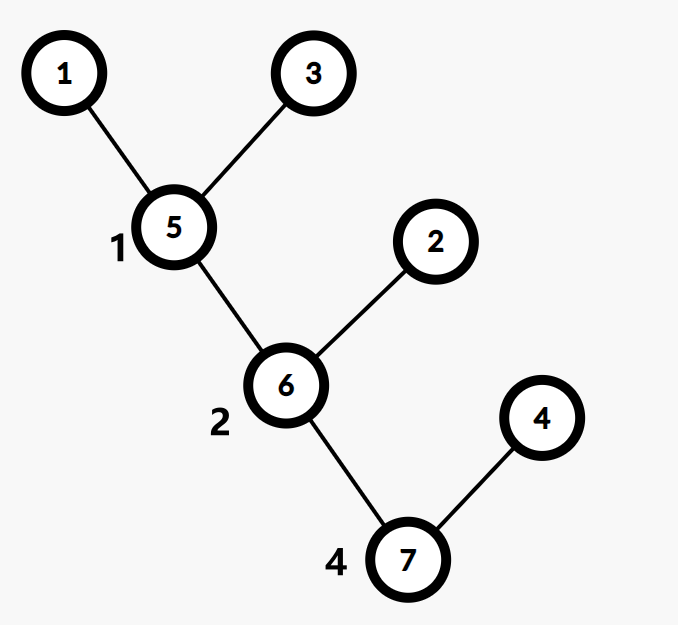
合并 \(1,3\) 时,新建点权为 \(1\) 的节点 \(5\) ,连接 \(1,5\),\(3,5\)
合并 \(2,3\) 时,新建点权为 \(2\) 的节点 \(6\) ,连接 \(2,6\),\(3,6\)
合并 \(3,4\) 时,新建点权为 \(4\) 的节点 \(7\) ,连接 \(3,7\),\(4,7\)
最后构造出的 \(Kruskal\) 重构树 如下:
若有 \(n\) 个点,这样构造一棵 \(Kruskal\) 重构树的时间复杂度是 \(O(n\log n)\) 的
性质
-
树上除叶子结点以外的点都对应着原来图中的边,叶子结点就是原来图上的节点
-
从每个点到根节点上除叶子结点外按顺序访问到的点的点权是单调的
-
出于 \(Kruskal\) 算法贪心的性质,两个点 \(u\) 和 \(v\) 的 \(lca\) 的点权就对应着它们最小生成树上的最大值,也是原图中两个点之间的所有简单路径上最大边权的最小值
-
这棵树是一个二叉堆
习题
P4768 归程
题意:
\(n\) 个点,\(m\) 条边,保证图联通,每条边有两个权值,一个长度 \(l\),一个海拔 \(y\)
多组询问,告诉你起点和水位线,小于等于水位线的边都会被淹没,只能走路,否则可以开车
问从当天起点到1号节点最少步行经过的长度,有些询问会强制在线
思路:
从 \(x\) 到 \(1\) 最小步行的长度 \(= \min\left\{dis(1,y)\right\}\),前提是 \(x\) 到 \(y\) 的路上海拔全大于 \(S\)
那么可以先跑一边从 \(1\) 到其他所有点的最短路
注意这里要用 \(dijkstra\) 因为 \(SPFA\) 死了
然后问题就转变为求 存在一条到 \(x\) 的路径海拔均大于 \(S\) 的点 \(y\) 组成的集合中 \(dis(1,y)\) 的最小值
很显然可以用 \(Kruskal\) 重构树了
我们先按照边的海拔值从大到小排序,然后跑一遍 \(Kruskal\) 重构树
这样对于树内的每一个节点 \(x\) ,他的所有祖先的海拔值自下而上递减
并且对于每一个节点 \(x\) 记录 \(d(x)\) 表示其子树内到 \(1\) 距离的最小值
搞一下倍增,找到 \(x\) 最上的祖先 \(y\) 使得 \(a(y)>S\) 且 \(a(fa(y))\leq s\)
这样 \(y\) 的子树内都是可以通过 \(x\) 开车到达的点
\(d(y)\) 即为答案
这样时间复杂度是 \(O(T\times (n+m+q)\log n)\)
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
#define pb push_back
#define mp make_pair
#define pii pair <int,int>
#define int long long
const int N=6e5+5;
const int M=1e6+5;
const int inf=1e18;
struct edge{
int x,y,l,a,id;
bool operator < (const edge X) const{
return a>X.a;
}
}e[M];
struct node{
int x,d;
bool operator < (const node X) const{
return d>X.d;
}
};
int n,m,rt;
int q,k,s,lastans;
int f[N][20],g[N],son[N][2];
int dep[N],v[N],d[N];
bool vis[N];
vector <pii> G[N];
inline void dijkstra(){
priority_queue <node> q;
for(int i=2;i<=2*n;++i) d[i]=inf,vis[i]=0;
d[1]=0;
q.push({1,0});
while(!q.empty()){
int x=q.top().x;
q.pop();
vis[x]=1;
for(auto y:G[x]){
int to=y.first,val=y.second;
if(vis[to]) continue;
if(d[to]>d[x]+val){
d[to]=d[x]+val;
q.push({to,d[to]});
}
}
}
}
inline int get(int x){
return x==g[x]?x:g[x]=get(g[x]);
}
inline void kruskal(){
int num=0;
sort(e+1,e+m+1);
for(int i=1;i<=2*n;++i) g[i]=i;
for(int i=1;i<=m;++i){
int x=e[i].x,y=e[i].y,l=e[i].l,a=e[i].a,id=e[i].id;
int fx=get(x),fy=get(y);
if(fx==fy) continue;
g[fy]=g[fx]=f[fx][0]=f[fy][0]=++rt;
son[rt][0]=fx,son[rt][1]=fy;
f[rt][0]=0;
v[rt]=a;
++num;
if(num==n-1) break;
}
}
inline int dfs(int x,int fa){
dep[x]=dep[fa]+1;
for(int i=1;i<=19;++i) f[x][i]=f[f[x][i-1]][i-1];
if(son[x][0]) d[x]=min(dfs(son[x][0],x),d[x]);
if(son[x][1]) d[x]=min(dfs(son[x][1],x),d[x]);
return d[x];
}
inline int query(int x,int y){
for(int i=19;i>=0;--i)
if(dep[x]>(1<<i)&&v[f[x][i]]>y) x=f[x][i];
return d[x];
}
inline void solve(){
memset(f,0,sizeof(f));
memset(son,0,sizeof(son));
n=read(),m=read();rt=n;
for(int i=1;i<=n;++i) G[i].clear();
for(int i=1;i<=m;++i){
int x=read(),y=read(),l=read(),a=read();
e[i]=(edge){x,y,l,a,i};
G[x].pb(mp(y,l));
G[y].pb(mp(x,l));
}
dijkstra();
kruskal();
dfs(rt,0);
q=read(),k=read(),s=read();
lastans=0;
while(q--){
int x=read(),y=read();
x=(k*lastans+x-1)%n+1,y=(k*lastans+y)%(s+1);
lastans=query(x,y);
printf("%lld\n",lastans);
}
}
signed main(){
int T=read();
while(T--)
solve();
}
标签:重构,const,int,Kruskal,点权,节点 来源: https://www.cnblogs.com/into-qwq/p/16451336.html