Manacher

Manacher

题意 :

求最长回文串

预处理 :

奇回文串的对称中心是中间的字符，偶回文串对称中心是中间两个字符的空隙处，若分开处理很麻烦，因此在每两个字符中间插入一个字符|使得对称中心都为一个字符

算法 :

定义 p[i] : 以 i 为回文中心的最长回文半径 ( p[i]-1 为最长回文串的长度 )

定义 mx 和 mid : 目前找到的回文串的右端的最右是mx，中心是mid

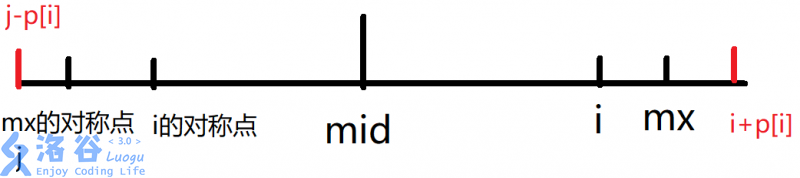
以i的对称点为回文中心的字符串 \(=\) 以i为回文中心的字符串，因此p[i]可以等于p[j]

但是由于超过mx的部分（即右红边部分）不能保证必定等于左红边的部分，所以p[i]不能超过mx-i

时间复杂度 : \(O(n)\)

code :

#include <bits/stdc++.h>
using namespace std;

const int N=11000005;

#define re register

int n,m,p[N*2],ans=1;
char a[N],s[N*2];

inline void make_s(){
	s[0]='$',s[1]='|';
	for(re int i=0;i<n;++i){
		s[m++]=a[i];
		s[m++]='|';
	}
	s[m]='%';
	n=m;
}

inline int manacher(){
	int mid=1,mx=1;
	for(re int i=1;i<n;++i){
		if(i<mx)
			p[i]=min(p[mid*2-i],mx-i);
		else
			p[i]=1;
		for(;s[i+p[i]]==s[i-p[i]];++p[i]);
		if(p[i]+i>mx){
			mx=p[i]+i;
			mid=i;
		}
		ans=max(ans,p[i]-1);
	}
	return ans;
}

signed main(){
	scanf("%s",a);
	n=strlen(a);
    m=2;
	make_s();
	cout<<manacher();
}

标签：字符,int,Manacher,mid,ans,mx,回文
来源： https://www.cnblogs.com/into-qwq/p/16437063.html