首页 > 其他分享> > lyndon 分解学习笔记

lyndon 分解学习笔记

2022-06-28 09:37:16 作者：互联网

lyndon 分解学习笔记

定义

lyndon 串

一个字符串，如果他是他的最小后缀，那么他就是 lyndon 串。

还有一种定义是，在他的循环同构里他是字典序最小的那个。

近似 lyndon 串

设 $t$ 是一个 lyndon 串，$t^c$ 为 $t$ 拼接 $c$ 次，$t'$ 为 $t$ 可空前缀，那么 $t^c + t'$ 为近似 lyndon 串。

lyndon 分解

将一个字符串分解为若干个字典序非严格递减的 Lyndon 串。

也就是将 $s$ 分解为 $s=t_1+ t_2+ \dots+ t_n$，使得每个 $i\in[1, n]$，$t_i$ 为 lyndon 串，并且 $t_i \geq t_{i + 1}$。

一些规定

$pre(s, x)$ 表示 $s$ 的长度为 $x$ 的前缀，$suf(s, x)$ 表示 $s$ 的长度为 $x$ 的后缀。

真前缀真后缀不是他本身。

性质

引理 1

若两个字符串 $u, v$ 均为 lyndon 串，并且 $u < v$，那么 $uv$ 都为 lyndon 串。

证明：

需要按长度进行分类讨论。

$1.$ $|u| > |v|$，因为 $v$ 是 lyndon 串，所以 $v$ 的所有后缀都大于 $v$，那么只证明 $uv < v$ 就好了，又因为 $u < v$ 已知，那么 $uv < v$。

$2.$ $|u| \leq |v|$，首先和上面一样，$uv$ 中 $v$ 是 lyndon 串，那么 $v$ 的所有后缀都大于 $v$，仍然只用证明 $uv < v$，但是此时 $|u| \leq |v|$ 有点难受。

首先你看 $u$ 是不是 $v$ 的前缀，如果 $u$ 不是 $v$ 的前缀，那么 $u < v$ 就比较出答案了，所以 $uv < v$。
如果 $u$ 是 $v$ 的前缀，那么 $u< v$ 的原因是因为他是前缀，后面是空的，所以没法比较了，那么这个时候是 $v$ 和 $v$ 的一段后缀去进行比较。

又因为，我们已知 $v$ 是一个 lyndon 串，根据我们之前的定义，$v$ 比他的任何一段后缀的字典序都要小，那么性质证毕。

引理 2

lyndon 分解具有唯一性，一个串的 lyndon 分解是唯一的。

证明：

考虑反证法，假设存在两种及以上的方式使得 lyndon 分解不唯一。

那么 $s= t_1 + t_2 + \dots + t_n = t'_1+t'_2 + \dots + t'_m$。

假设第一次不相同的 lyndon 串位置为 $i$，假设 $|t_i| > |t'_i|$，那么 $t_i > t'_i$。

令 $t_i = t'_i+t'_{i+1} + \dots + t'_m + pre(t'_{k+1}, l)$，那么根据定义，$t_i < pre(t'_{k + 1}, l) \leq t'_{k + 1} \leq t'_i < t_i$，推出矛盾。

所以分解一定唯一！

引理 3

lyndon 分解具有存在性，每个字符串都存在 lyndon 分解。

证明：

显然。

引理 4

如果字符串 $v(|v| = r - 1)$ 和字符串 $c(|c| = 1)$，满足 $vc = pre(s, r)$，并且 $s$ 为一个 lyndon 串，那么对于一个字符串 $d(d > c 且 |d| = 1)$ ， $vd$ 为一个 lyndon 串。

证明：

首先考虑一个 lyndon 串的前缀是啥玩意。

好像啥也不是，一个 lyndon 串的前缀也不一定是一个 lyndon 串。

分类讨论一下，如果这个前缀本身是一个 lyndon 串了，那么显然成立，因为最后一个字符的字典序反而被升高了。

如果这个前缀不是一个 lyndon 串。

就你考虑那么他一定是加入的这个字符 $c$ 让他不是 lyndon。

否则，如果是在之前的话，那么这个前缀最后会是一个 lyndon。

因此变大之后，仍然是个 lyndon。

引理 5

设三个字符串 $s_1>s_2>s_3$，其中 $s_1$ 是 lyndon 串，那么 $s_1 > s_2^2 \geq s_2 + s_3$。

证明：

如果 $s_2$ 为 $s_1$ 的后缀，那么根据定义 $s_1 > pre(s_1,|s_2|) > s_2 \geq s_3$。

如果 $s_2$ 不为 $s_1$ 的后缀，这东西绝对成立啊（

性质 1

一个 lyndon 串不会存在 border。

证明：

如果存在 border，那么 border 就是最小后缀，这个串就不是 lyndon 串。

性质 2

假设 lyndon 串 $s = uv$，并且 $|u| > 0, |v| > 0$，那么 $u < v$。

性质 3

如果 $|s| > 2$，$s$ 是一个 lyndon 串的充要条件是 $s = uv$，且 $|u| > 0$,$|v| > 0,u < v$，并且 $u$ 和 $v$ 都是 lyndon 串。

证明：

充分性是引理 $1$。

必要性：去看 sh 写的吧 orz

算法

如何将一个串 $s$ 进行 lyndon 分解。

后缀数组解法

我们可以先跑一遍后缀数组，设 $a_i$ 表示最小的 $j$ 使得 $s[j\dots n] < s[i \dots n]$。

那么一开始你在 $a_1$ 的位置切一下，然后继续往后考虑后面的串就好了。

实现的时候，可以按后缀数组的 rank 加入，用 set 维护后面比它小的最前面的，然后将其设为新的开头继续做，通过这种方法，我们还可以知道每一个后缀的 lyndon 分解。

然后甚至你发现这东西构成了一个树形关系，或许可以有很优雅的性质。

复杂度是 $n\log(n)$ 的，可能会被卡，所以我也没写（雾），不过这东西挺好写的吧。

Duval 算法

这是专门求解 lyndon 分解的算法。

将整个串分成 $3$ 部分，$s_1 + s_2 + s_3$，其中 $s_1$ 为已经完成的分解，$s_2$ 为正在分解的，$s_3$ 为还未分解的。

这个部分我们可以通过两个指针进行划分。

其中 $s_2$ 表示为 $w^k + p$，其中 $p$ 是 $w$ 的一个可空真前缀。

维护 $s_3$ 的第一个字符位置 $k$，以及 $s_1$ 的最后位置 $i$ 表示 $[1 \dots i]$ 被分解完毕。

令 $j = $k - |w|$，那么加入 $k$ 的时候，比较 $S_j$ 和 $S_k$ 的关系。

如果 $S_j < S_k$ 那么将 $w$ 变成 $[i, k]$，也就是 $j := i,k:=k+1$。

如果 $S_j = S_k$，那么 $s_2$ 作为一个 $lyndon$ 串的性质仍然成立，$j:=j +1,k:=k+1$。

如果 $S_j > S_k$，那么 $[i, i + |w|), [i+|w|, i + 2|w|) \dots$ 会是若干个 lyndon 分解。

每个字符最多被遍历 $3$ 次，复杂度为 $O(n)$。

贴个代码。

  cin >> (S + 1);
  int n = strlen(S + 1), ans = 0, i = 1;
  while (i <= n)  {
    int j = i, k = i + 1;
    while (S[j] <= S[k]) {
      if (S[j] == S[k])  ++j, ++k; 
      else j = i, ++k;
    }
    // S[j] > S[k]，s2被当成若干个 lyndon 分解
    int len = k - j; // 这些 lyndon 的串长
    while (i <= j) {
      // i 为左端点，i + len - 1 为右端点
      // ans ^= (i + len - 1);
      cout << i + len - 1 << " " ;
      i += len;
    }
  }

最小表示法

一个字符串的最小表示被定义为其所有循环同构里字典序最小的串。

我们发现这和上面给出的 lyndon 串的另一种定义相符的。

于是我们可以将串复制一遍接在末尾成为串 $t$，对 $t$ 进行 lyndon 分解，找到首字母位置 $\leq n$ 且最大的 lyndon 串。

模板题目是 $\text{Luogu P1368}$。

贴个代码：

  cin >> n;
  rep (i, 1, n)  cin >> S[i];
  int ans = 0, i = 1;
  rep (i, n + 1, n + n)  S[i] = S[i - n];
  while (i <= n)  {
    int j = i, k = i + 1;
    ans = i;
    while (S[j] <= S[k] && k <= n * 2) {
      if (S[j] == S[k])  ++j, ++k; 
      else j = i, ++k;
    }
    int len = k - j;
    while (i <= j)  i += len;
  }
  rep (i, 1, n)  cout << S[ans + i - 1] << " ";

例题 Luogu P5334 [JSOI2019]节日庆典

题目大意：给定一个串 $S$，求每个前缀的最小表示法。

考虑 lyndon 分解，如果我们对每个前缀都跑一边 lyndon 分解的话，答案应该是最后一个开头 $\leq i$ 的 lyndon 串。

这样不优秀啊，但是我们仍然考虑 lyndon 分解。

假设我们现在维护的是 $pu^tv$，仍然维护指针 $i,j,k$。

我们其实当前位置要加入的一个字符 $k$ 的最小表示法的开头只会有两种情况，一种是在我的当前开始的位置 $i$，一种是在我加入的这个 $v$ 里面的。

在 $v$ 里面的话，你考虑他最终的表示法会是什么样子，比如 $pu^tv$，那么最终他会是 $vpu^t$。

你仔细发现，反正我没发现，然后你发现如果你去掉最后的 $|u|$ 个字符，他就会变成 $vpu^{t-1}$，然后这就是一个已经求解过的答案了，他是 $pu^{t-1}v$ 的最小表示法。

现在我们需要根据 $S_j$ 和 $S_k$ 的大小进行分类。

如果 $S_j < S_k$，那么根据 lyndon 串的性质，那么 $u^tv+S_k$ 仍然是一个 lyndon 串，那么此时的 $i$ 就是我们的 $ans_k$。

如果 $S_j > S_k$，那么之前的 lyndon 串被划分了出来，但是当前位置仍然不知道，于是我们将其放到后面进行求解。

如果 $S_j = S_k$，那么可以选择两种位置，首先就是当前的 $i$ 可以作为 $ans_k$，另一种是，先前循环节中 $k$ 的对应位置 $j$ 的答案向后移一个循环节的对应位置 $ans_j + k - j$。

然后需要对这两个部分进行取 $\min$ 判断，我们知道 $z$ 函数是可以通过 $O(n)$ 的预处理做到线性复杂度进行预处理一个字符串和他每个后缀的 $lcp$。

令 $x = i, y = ans_j + k - j,R = k$。

那么需要比较的为 $S[i\dots k] + S[1 \dots (i - 1)]$ 和 $S[(ans_j + k - j) \dots k] + S[1\dots ans_{j} + k - j - 1]$ 的字典序大小。

首先我们只会在 $S_j = S_k$ 的时候遇到这种情况，那么 $S[i \dots (i + k - (ans_j + k - j))]$ 和 $S[(ans_j + k - j) \dots k]$ 肯定都是相同的。

如下图：

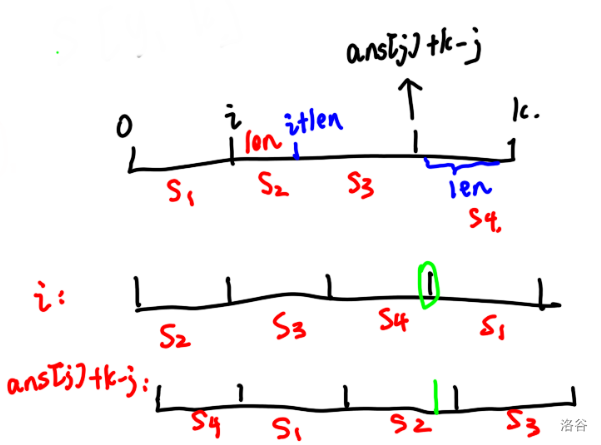
也就是说上面的 $S_2$ 和 $S_4$ 一定是相同的。

然后你分着来比较，先比较 $S_3 + S_4$ 和与他对应长度的那一部分。

也就是图中画着绿线的那一部分，然后再比较后面的剩下部分就好了。

这样你发现，每次都是将一个子串 $S[a \dots b]$ 与原串的一个前缀 $S[1 \dots b - a + 1]$ 进行比较。

那么我们可以使用 $z$ 函数，判断后缀 $a$ 与原串的一个 lcp 长度判断是否再比较范围内，并找到这个不同即可。

使用 $\text{exkmp}$ 可以求解。

于是直接跑 Duval 算法就好了，复杂度 $O(n)$，真神仙。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
// Problem: P5334 [JSOI2019]节日庆典
// Contest: Luogu
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// The Author : Pt

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
using namespace std;
namespace io {
  const int SIZE = (1 << 21) + 1; char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55]; int f, qr;
  #define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
  inline void flush () {  fwrite (obuf, 1, oS - obuf, stdout); oS = obuf; }
  inline void putc (char x) { *oS ++ = x; if (oS == oT) flush (); }
  template <class I> inline void gi (I &x) { for (f = 1, c = gc(); c < '0' || c > '9'; c = gc()) if (c == '-') f = -1; for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15); x *= f; }
  string getstr(void) { string s = ""; char c = gc(); while (c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF) c = gc(); while (!(c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == EOF))s.push_back(c), c = gc(); return s;}
  template <class I> inline void print (I x) { if (!x) putc ('0'); if (x < 0) putc ('-'), x = -x; while (x) qu[++ qr] = x % 10 + '0',  x /= 10; while (qr) putc (qu[qr --]); }
  struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
}
using io :: gi;  using io :: putc;  using io :: print;
#define V inline void
#define I inline int
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
const int N = 3e6 + 5;
char S[N];
int z[N], n, ans[N];
void exkmp() {
  z[1] = n;
  for (int i = 2, l = 0, r = 0; i <= n; i++) {
    if (i <= r)  z[i] = min(z[i - l + 1], r - i + 1);
    while (i + z[i] <= n && S[i + z[i]] == S[1 + z[i]]) ++ z[i];
    if (i + z[i] - 1 > r)  r = i + z[l = i] - 1;
  }
}
int compare(int x,int y,int r) {
  if (x == y)  return x;
  int zz = z[x + r - y + 1];
  if (zz < y - x)  return S[x + r - y + 1 + zz] < S[1 + zz] ? x : y;
  zz = z[y - x + 1];
  if (zz < x - 1)  return S[1 + zz] < S[y - x + 1 + zz] ? x : y;
  return x;
}
void solve() {
  int i = 1;
  while (i <= n) {
    int j = i, k = i + 1;
    if (!ans[i])  ans[i] = i;
    while (k <= n && S[j] <= S[k]) {
      if (S[j] < S[k]) {
        if (!ans[k])  ans[k] = i;  j = i;  ++k;
      }  else {
        if (!ans[k]) {
          if (ans[j] < i)  ans[k] = i;
          else  ans[k] = compare(i, ans[j] + k - j, k);
        }
        ++k;  ++j;
      }
    }
    int len = k - j;
    while (i <= j)  i += len;
  }
}
signed main () {
#ifdef LOCAL_DEFINE
  freopen("input.txt", "r", stdin);
#endif
  cin >> (S + 1);  n = strlen(S + 1);
  exkmp();  solve();
  rep (i, 1, n)  cout << ans[i] << " ";
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

参考的神仙资料

https://www.cnblogs.com/chenxiaoran666/p/Luogu5334.html

https://www.luogu.com.cn/blog/blog10086001/qian-tan-lyndon-word

fsy 哥哥的讲课内容。

标签：dots,int,笔记,后缀,分解,lyndon,丽莎
来源： https://www.cnblogs.com/ptno/p/16418308.html