Baozi Training Leetcode solution 2304. Minimum Path Cost in a Grid

Problem Statement 

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

 

Example 1:

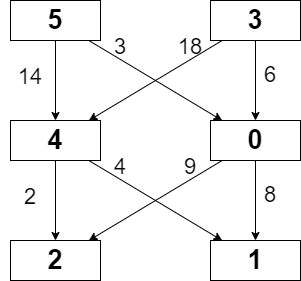
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid consists of distinct integers from 0 to m * n - 1.
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

 Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

A classic DP problem (Dynamic Programming) because it's either ask you a boolean yes or no questions, Or ask for extreme values, e.g., min, max

• Build up a minCost 2 day array, each array element denotes by far the min cost to reach to that element
• Make sure to initialize the values.

 

 

 

Solutions

 1 public int minPathCost(int[][] grid, int[][] moveCost) {
 2     if (grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0 || moveCost == null) {
 3         return -1; // or throw exception
 4     }
 5 
 6     int[][] minCost = new int[grid.length][grid[0].length];
 7     for (int i = 0; i < minCost[0].length; i++) {
 8         minCost[0][i] = grid[0][i];  // first row costs are the init values
 9     }
10 
11     for (int i = 1; i < minCost.length; i++) {
12         for (int j = 0; j < minCost[0].length; j++) {
13             int min = Integer.MAX_VALUE;
14             for (int k = 0; k < minCost[0].length; k++) {
15                 min = Math.min(min, minCost[i - 1][k] + moveCost[grid[i - 1][k]][j]);
16             }
17             minCost[i][j] = grid[i][j] + min;
18         }
19     }
20     int finalMin = Integer.MAX_VALUE;
21 
22     for (int i = 0; i < minCost[0].length; i++) {
23         finalMin = Math.min(minCost[minCost.length - 1][i], finalMin);
24     }
25     return finalMin;
26 }

 

 

  Time Complexity: O(N^3) since going through the 2-d array and another nested loop
Space Complexity: O(N^2) used the 2-d minCost array

References

• None

标签：Training,int,minCost,2304,solution,moveCost,length,cost,grid
来源： https://www.cnblogs.com/baozitraining/p/16410625.html