[HNOI2002]公交车路线
作者:互联网
[HNOI2002]公交车路线
注:今天做到的有点意思的题目。
题意简述
有\(8\)个站点,从\(A\) 出发一共走\(n\) 步到\(E\)(中途不可经过\(E\)),问一共有多少种走法?
图:
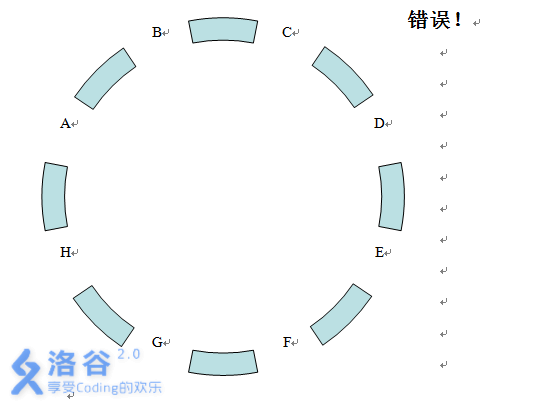
思路一:矩阵(假弗洛伊德)
这个题感觉和矩阵半毛钱关系都没有,那可能用矩阵?
不过不慌哈,让我们细细道来。
我们设\(dp[i][j]\) 为从\(i\)到 \(j\)有\(m\)种方式。
\[\notag 当走每一步时,都有以下转移方程:\\ dp[i][j] = \sum\limits _{k=1}^{n} dp[i][k]*dp[k][j] \]这是显然的,因为此时从 \(i\) 到 \(k\) 有 \(dp[i][k]\) 种方式,从 \(k\) 到 \(j\) 有 \(dp[k][j]\) 种方式,乘法原理一下,就可以得到以上方程。
题外话:不知各位是否有一种熟悉的感觉,看看以下式子(弗洛伊德):
\[\notag dis[i][j] = \sum\limits _{k=1}^{n} \min(dis[i][k]+dis[k][j],dis[i][j]) \]嘿嘿,好了回到这个题。
上面这个式子又和矩阵有什么关系呢?
让我们先看看矩阵乘法的表达式:
\[\notag A(n*n),B(n*n)\\ C=AB\\ C[i][j]=\sum\limits _{k=1}^{n} A[i][k]*B[k][j] \]emm....不能说一模一样吧,但可以说完全一致。
所以结果就显然了。
但是!还没有完,我们只有转移方程但没有最开始的矩阵,就像数学归纳法一样只有\(n>=2\)时成立,但\(n=1\)时不成立又有什么用呢?
以下依据 \(dp[i][j]\) 为从\(i\)到 \(j\)的方式给出基础矩阵:
\[\notag \begin{bmatrix} Z&A&B&C&D&E&F&G&H\\ A&0&1&0&0&0&0&0&1\\ B&1&0&1&0&0&0&0&0\\ C&0&1&0&1&0&0&0&0\\ D&0&0&1&0&1&0&0&0\\ E&0&0&0&0&0&0&0&0\\ F&0&0&0&0&1&0&1&0\\ G&0&0&0&0&0&1&0&1\\ H&1&0&0&0&0&0&1&0\\ \end{bmatrix} \]解释:行表示出发点,列表示到达到点,其中由于不可以经过\(E\)所以\(E\)所在行为\(0\)。
时间复杂度
\(O(8^2\log n)\)
CODE
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn = 5e5+32;
ll int_maxn=1e9;
ll ll_maxn=1e18;
inline ll read_int(){
ll a=0,f=0,g=getchar();
while(g<'0'||g>'9'){if(g=='-') f=1;g=getchar();}
while('0'<=g&&g<='9') a=a*10+g-'0',g=getchar();
return f ? -a : a;
}
inline void write(ll s,bool f,int cnt=0){
ll top=0,a[40];
if(s<0) s=-s,putchar('-');
while(s) a[++top]=s%10,s/=10;
if(top==0) a[++top]=0;
while(top) putchar(a[top]+'0'),top--;
if(f) putchar('\n');
while(cnt--) putchar(' ');
}
const int maxm=10;
int lin[9][9]={
// a b c d e f g h
0,0,0,0,0,0,0,0,0,
0,0,1,0,0,0,0,0,1,
0,1,0,1,0,0,0,0,0,
0,0,1,0,1,0,0,0,0,
0,0,0,1,0,1,0,0,0,
0,0,0,0,0,0,0,0,0,
0,0,0,0,0,1,0,1,0,
0,0,0,0,0,0,1,0,1,
0,1,0,0,0,0,0,1,0,
};
int mod=1000;
struct Matrix{
ll n,m;
ll matrix[maxm][maxm];
inline void clear(){n=m=0,memset(matrix,0,sizeof matrix);}
inline void jc(ll M){
clear();
n=m=M;
for(ll i=1;i<=n;i++) matrix[i][i]=1;
}
Matrix operator * (Matrix a)const{
Matrix b;
b.clear();
b.n=n,b.m=a.m;
for(ll i=1;i<=b.n;i++){
for(ll e=1;e<=b.m;e++){
for(ll k=1;k<=m;k++){
b.matrix[i][e]+=matrix[i][k]*a.matrix[k][e];
b.matrix[i][e]%=mod;
}
}
}
return b;
}
friend inline Matrix qpow(Matrix a,ll C){
Matrix base;
base.jc(a.n);
while(C){
if(C&1) base=base*a;
a=a*a,C>>=1;
}
return base;
}
inline void write_(bool a){
if(a) write(n,0),putchar(' '),write(m,1);
for(ll i=1;i<=n;i++){
for(ll e=1;e<=m;e++){
write(matrix[i][e],0),putchar(' ');
}
puts("");
}
}
inline void td(){
clear();
n=m=8;
for(int i=1;i<=8;i++){
for(int e=1;e<=8;e++){
matrix[i][e]=lin[i][e];
}
}
}
inline int add_m(int cnt){
ll ans=0;
for(int i=1;i<=n;i++){
ans+=matrix[i][cnt];
ans%=mod;
}
return ans;
}
};
inline void read(){
int n=read_int();
Matrix A;
A.td();
A=qpow(A,n);
write(A.matrix[1][5],1);
}
int main (){
read();
}
思路二:DP
注:转自题解。
时间复杂有点高(相对于上一个来说):\(O(n)\)
我们把\(E\)去掉,这个系统分成了以\(A\)为中心的完全对称的列。
我们记\(dp[i][j]\)表示第\(i\)站在\(j\)次乘坐后到达的方案数。
因为每次只能从相邻的站到达,那么第\(N\)次到达\(E\)的方案数等于第\(N-1\)次到达\(D\)和\(F\)的方案数。
以此类推\(dp[i][j]=dp[i-1][j-1]+dp[i+1][j-1]\) 这里的\(i-1\)\(,\)i+1$表示相邻的站。
之前说过以\(A\)为中心完全对称,所以\(D\)和\(F\),\(C\)和\(G\)......的方案数完全相同,只需算一边。
仔细观察,每个状态只与上一个状态有关,因此可以压位为\(dp[4][2]\)
CODE
#include<iostream>
using namespace std;
int dp[4][2]; //具体含义如上所述
int main()
{
fill(dp[0],dp[0]+4*2,0);
dp[0][0]=1;
int N,pos=0;
cni>>N;
for(int k=1;k<N;k++)
{
pos=pos^1;
dp[0][pos]=2*dp[1][pos^1]%1000; //A处的方案等于两边的方案相加,由于相等只算一边的*2
dp[1][pos]=(dp[0][pos^1]+dp[2][pos^1])%1000;
dp[2][pos]=(dp[1][pos^1]+dp[3][pos^1])%1000;
dp[3][pos]=dp[2][pos^1]; //D只能由C来
}
cout<<2*dp[3][pos]%1000<<endl; //E由D和F来
return 0;
}
标签:公交车,int,ll,矩阵,notag,路线,HNOI2002,dp,dis 来源: https://www.cnblogs.com/LQX-OI/p/16391467.html