首页 > 其他分享> > 【计算机基础】计算机原理-浮点数存储

【计算机基础】计算机原理-浮点数存储

2022-06-16 01:31:08 作者：互联网

原文：https://www.taowong.com/blog/2018/07/10/principle-of-computer-float-num.html

1、精度丢失

作为程序员大家应该都遇到过下面这种情况，用浮点数做运算，发现结果与预期有偏差，比如下面的JAVA代码

public static void main( String[] args )
    {
    	 int i = 3;
    	 float j = 0.9f;
    	 System.out.println("3乘以0.9的结果是：" + i*j);
    }

用一个整数3乘以浮点数0.9，期望结果是2.7，实际结果却是

20180227004

与2.7相差0.0000002，这道连小学生都不会算错的题目，为什么计算机会算错？真正的原因要从计算机保存浮点数的底层原理说起。

2、计算机如何保存浮点数

2.1、二进制小数

在计算机中数字使用二进制方式存储，所以理解浮点数的第一步是理解如何用二进制表示小数。

首先，对于我们比较了解的十进制，可以使用下面的公式表示：

d_md_m-1···d₁d₀.d_-1d_-2···d_-n

d的取值范围是0-9的任意数字。 m则从左向右依次递减，在小数点左边m=0，小数点右边m=-1。

在小数点左边的数字，取10的m次正幂，得到整数。小数点右边则取10的m次负幂，得到小数。例如12.34 表示数字

同样的，二进制小数也可以用类似方式表示，b的取值范围变成了0-1，小数点左边计算2的m次正幂，右边计算2的m次负幂。例如101.11 表示数字

但是这种表示方法并不完美，存在两个缺陷。

1) 无法准确的表示所有数字。

例如十进制小数0.20，我们无法通过二进制小数来准确表示，只能不断增加二进制长度来提高精度。

二进制	值	十进制
0.0		0.0
0.01		0.25
0.0011		0.1875
0.001101		0.203125
0.00110011		0.19921875

从上图可以看到，数字的值在不断的接近0.20，但是始终存在偏差。

2) 无法有效表示非常大的数字。

例如表达式 5×2^100 是二进制101后面跟了100个0，如果用上面的方式表示非常浪费空间。

因此，人们需要一种更加简洁的方式来表示浮点数。1985年，Intel公司赞助美国加州大学的William Kahan教授，设计了一套处理器浮点数标准，这个标准最终被IEEE(电气和电子工程师协会)借鉴，制定出IEEE浮点标准。目前，所有的计算机都支持这个标准。

2.2、IEEE 浮点标准

根据IEEE 浮点标准，任意一个二进制浮点数V可以表示成下面的形式：

V = (-1)^s × 2^E ×M

符号(sign) s表示符号位，当s=0，V为正数；当s=1，V为负数。

尾数(significand) M是一个二进制小数，1≤M<2。

阶码(exponent) E的作用是对浮点数加权，这个权重是2的E次幂(可能是负数)

比如十进制的11.0，写成二进制就是1011.0，用IEEE标准表示就是(-1)^0 × 1.011 × 2^3 ，s=0，M=1.011，E=3。

那么，计算机是如何存储s，M，E这三个值呢？如果是一个单精度(32位)浮点数，计算机会在内存中开辟一个32位的存储空间，最高1位保存s，中间8位保存E，最后23位保存M。

20180227001

如果是一个双精度(64位)浮点数，则开辟64位的存储空间，最高1位保存s，中间11位保存E，最后52位保存M。

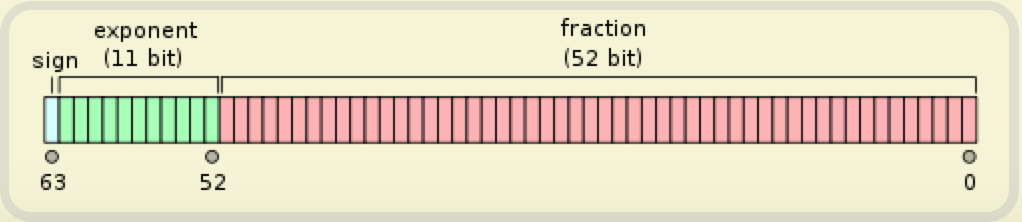
20180227002

对于符号s，存储值非0即1。

对于尾数M，只保存后面的小数部分。这是由于1≤M<2，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，这样做的好处是可以节省一位有效数字。

而对于阶码E，情况较为复杂。

首先，E要通过中间值换算得到真实值。这是由于E要能够表示负数，也就是负次幂。而E本身是无符号的，因此IEEE浮点标准规定，在计算真实值时，E要减去一个中间值。单精度情况下，E减去127，双精度情况下，E减去1023。

以二进制数1011.0为例，E的真实值是3，但是存储在计算机中是3+127=130(单精度)，换算成二进制就是10000010。

另外，当E的值不同时，对最终结果计算方法也不一样，一共有下面三种情况。

1) 当E不全为0，也不全为1时。　表示规格化形式的数字。此时E减去中间值得到真实值，M的整数部分取1。

2) 当E全为0时。　表示非规格化形式的数字，主要是0或者非常接近于0的数。此时E减去中间值得到真实值，M的整数部分取0。

3) 当E全为1时。　表示特殊值。如果M全为0，表示±无穷大(正负取决于符号s），如果M不全为0，表示这不是一个数（NaN）。　

3、精度丢失的原因

了解了原理，现在我们可以开始分析精度丢失的原因，下面我们来模拟计算机的运算过程。

第一步，将十进制结果转换成二进制。文章开头的例子中，十进制结果是2.7，由于2.7无法用二进制精确表示，因此出现第一次精度丢失。

2.7 => 10.10110011001…

第二步，用IEEE标准表示二进制浮点数，得到s=0，M=1.010110011001…，E=1。

10.1011001… => (-1)^0 × 1.01011001… × 2^1

第三步，按照IEEE标准保存数据。此时是单精度浮点数，M只能保存小数点后23位，多余的部分被丢弃了，因此出现第二次精度丢失。下面是计算机中实际保存的结果。

1位	8位	23位	丢弃
0	10000000	01011001100110011001100	11001…

第四步，从内存中取出二进制数值，还原成十进制后显示在屏幕上。由于前面已经经历了两次精度丢失，因此还原出来的结果也就不正确了。

4、如何避免精度丢失

使用整数替代浮点数。二进制整数可以完整的表示所有十进制整数，不存在精度丢失问题，因此我们可以将小数位数固定或者较少的数字转换成整数存储。比如存储货币金额，如果存储单位是元，则需要保留两位小数，例如23.45元。如果将单位改成分，则可以完全使用整数存储，例如2345分。
使用特殊类处理高精度运算。例如JAVA中的Bigdecimal类。不过要注意，使用这些特殊类虽然可以解决精度问题，但有可能带来其它问题，JAVA中的Bigdecimal类在处理性能上就比float和double要低很多。

标签：表示,存储,计算机,二进制,浮点数,IEEE,精度,小数
来源： https://www.cnblogs.com/cdaniu/p/16380528.html