1245. 树的直径(拓扑排序+BFS)

1245. 树的直径

给你这棵「无向树」，请你测算并返回它的「直径」：这棵树上最长简单路径的 边数。

我们用一个由所有「边」组成的数组 edges 来表示一棵无向树，其中 edges[i] = [u, v] 表示节点 u 和 v 之间的双向边。

树上的节点都已经用 {0, 1, ..., edges.length} 中的数做了标记，每个节点上的标记都是独一无二的。

示例 1：

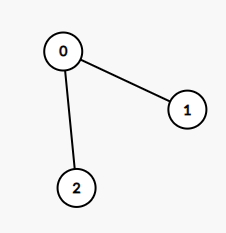
输入：edges = [[0,1],[0,2]]
输出：2
解释：
这棵树上最长的路径是 1 - 0 - 2，边数为 2。

示例 2：

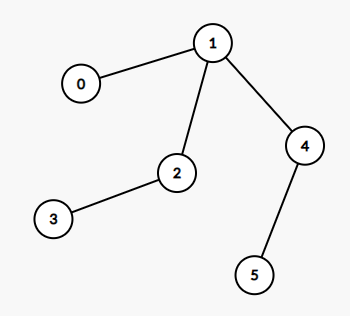
输入：edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
输出：4
解释： 
这棵树上最长的路径是 3 - 2 - 1 - 4 - 5，边数为 4。

提示：

• 0 <= edges.length < 10^4
• edges[i][0] != edges[i][1]
• 0 <= edges[i][j] <= edges.length
• edges 会形成一棵无向树

class Solution {
public:
    int treeDiameter(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<vector<int>> grap(n);
        vector<std::pair<int,int>> ans;
        vector<int> degree(n);
        // 构建无向图
        for(auto &edge : edges){
            grap[edge[0]].push_back(edge[1]);
            grap[edge[1]].push_back(edge[0]);
            degree[edge[0]]++;
            degree[edge[1]]++;
        }

        queue<int> q;
        for (unsigned int i = 0; i < degree.size(); i++) {
            // 针对无向图入度为1的入队
            if (degree[i] == 1) {
                q.push(i);
            }
        }
        int step = 0;
        while (q.size() > 2) { // 等于2时找到树的直径
            n -= q.size();
            int mSize = q.size();
            for (int i = 0; i < mSize; i++) {
                int cur = q.front();
                q.pop();
                degree[cur] = 0; // 防重复  
                for (auto &i : grap[cur]){
                    degree[i]--;
                    if (degree[i]==1) {//叶子节点入队列
                        q.push(i);
                    }
                }
            }
            step += 2;
        }
        return step + n - 1;
    }
};

标签：degree,int,拓扑,edge,BFS,grap,edges,1245,size
来源： https://www.cnblogs.com/MGFangel/p/16294292.html