前言

许久不写博客，趁着五一假期复习一下前面的知识点。

同样的，某些未额外注明的图片或者想法来自网络大佬，如有冒犯立即删除。

理解

积分的形式一般是这样的：

$\int_LF(x,y)\mathrm ds$

我们按两种方式，一步步分解。

面积理解

先考虑简单情况，按照二元函数讨论第一类曲线积分：

$F(x,y)$

这个函数表示了三维坐标系中的一个平面，应该不难理解。

随便画的 \(F(x,y) = \sin(x) \sin(y)+2\)

所以函数 \(F(x,y)\) 在这里的含义是：点\(F(x_a,y_a)\) 到 \(xoy\) 平面的距离（高度）。

那我们的积分区域是 \(L\).这是代表了什么呢？

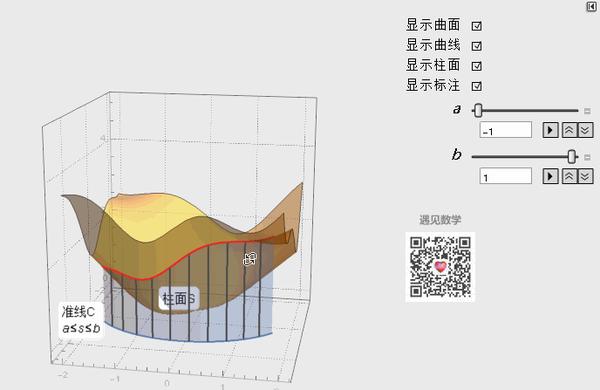
位于下面 \(xoy\) 平面的小弧线就是我们的积分区域 \(L\) 了。对应的 \(\mathrm ds\) 微元切割也能很容易地理解。
（如果不能理解那说明你的前置课程需要巩固一下了）

所以根据 \(F(x,y) \times \mathrm ds\) 可以理解为图中小竖条面积。因此取极限求和之后就会得到这一块积分区域下的异形曲面的面积了。这样我们把曲线积分变又回到了熟悉的曲线下面积的理解上来了。

线密度理解

而教材上面使用的 线密度 定义又是怎么来的呢？

假如我们将整个曲线（积分区域）压缩回二维（俯视图），那么 \(F(x,y)\) 去了哪里呢？
（麻烦各位自己想象一下把 \(x\) 轴拍扁的样子。。。不想做动图了）

隐藏的第三维——密度

现在想象 \(xoy\) 平面的俯视图上面的一条线，这代表了我们需要的积分区域 \(L\) 。在这里我们可以巧妙地将第三维映射到颜色上，用它来表示线密度。
因为我有点红绿色弱，所以我想规定：

$$颜色越红则线密度高，颜色越蓝则线密度低。中间色为紫色。$$

灵感来源于3b1b的 这个视频

（视频截图）

所以我们可以得到一张铺满整个二维坐标系的彩色的函数图片（只有红色和蓝色以及中间色紫色）。上面的每个点有三个坐标：x位置，y位置，颜色。写到函数里面看起来像这样：

$颜色 = F(位置x,位置y)$ $\rho = F(x,y)$

记得图像上面那一条代表了积分区域 \(L\) 的线吗？我们只需要沿着这条线对着颜色（密度）积分就能得到曲线积分了。

为什么我想用颜色可视化函数呢？因为好看啊！

计算

理解了曲线积分是怎么一回事之后我们就可以着手开始计算了。

变形

形式只需要记住：

$\int_LF(x,y)\mathrm ds = \int_L F(x,y)\sqrt{(dx)^2+(dy)^2}$

即可开始计算

我是怎么理解的？
后面的 \(ds\) 就相当于对弧长求微分，对弧长微分用直角三角形求长度就可以了。也不知道对不对

或者可以写成参数方程的形式：

$\int_LF(x,y)\mathrm ds = \int_\alpha^\beta F(\varphi(t),\psi(t))\sqrt{\varphi'^2(t)+\psi'^2(t)}$

注意：
曲线积分的下限一定小于上限。
如果曲线 \(L\) 平行于x或y坐标轴，则把函数中的y或x变为常数。

实际计算

绝大部分都需要转化为参数方程计算。一般会需要使用到：

$\cos x^2 + \sin x^2 = 1$ （记得配方变形）

如果积分曲线于圆相关，不妨尝试改变为极坐标：

x^2 + y^2 = a \Rightarrow r=a\cos\theta

熟悉计算后就像一般积分一样容易，只是多一步代换或者变形。

标签：int,积分,曲线,理解,第一类,ds,mathrm
来源： https://www.cnblogs.com/canisidea/p/first_line_intergral.html