DLX 学习笔记
作者:互联网
Dancing Links X
用来解决精确覆盖问题
正题
给定一个由 \(0-1\) 组成的矩阵,是否能找到一个行的集合,使得集合中每一列都恰好包含一个 \(1\)
考虑如下矩阵:
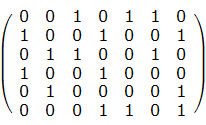
先假定选择第1行,如下所示:
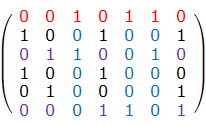
如上图中所示,红色的那行是选中的一行,这一行中有 \(3\) 个 \(1\) ,分别是第\(3\) 、\(5\) 、\(6\) 列。
由于这 \(3\) 列已经包含了 \(1\) ,故,把这三列往下标示,图中的蓝色部分。蓝色部分包含 \(3\) 个\(1\) ,分别在 \(2\) 行中,把这 \(2\) 行用紫色标示出来
根据定义,同一列的 \(1\) 只能有 \(1\) 个,故紫色的两行,和红色的一行的 \(1\) 相冲突。
那么在接下来的求解中,红色的部分、蓝色的部分、紫色的部分都不能用了,把这些部分都删除
得到一个新的矩阵
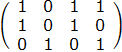
行分别对应矩阵 \(1\) 中的第\(2\)、\(4\)、\(5\)行
列分别对应矩阵 \(1\) 中的第\(1\)、\(2\)、\(4\)、\(7\)列
于是问题就转换为一个规模小点的精确覆盖问题
在新的矩阵中再选择第1行,如下图所示

还是按照之前的步骤,进行标示。红色、蓝色和紫色的部分又全都删除,导致新的空矩阵产生,而红色的一行中有 \(0\)(有 \(0\) 就说明这一列没有 \(1\) 覆盖)。说明,第 \(1\) 行选择是错误的
那么回到之前,选择第 \(2\) 行,如下图所示
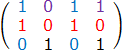
按照之前的步骤,进行标示。把红色、蓝色、紫色部分删除后,得到新的矩阵

行对应矩阵 \(2\) 中的第 \(3\) 行,矩阵 \(1\) 中的第 \(5\) 行
列对应矩阵 \(2\) 中的第 \(2\) 、 \(4\) 列,矩阵 \(1\) 中的第 \(2\) 、 \(7\) 列
由于剩下的矩阵只有 \(1\) 行,且都是 \(1\) ,选择这一行,问题就解决
于是该问题的解就是矩阵 \(1\) 中第 \(1\) 行、矩阵 \(2\) 中的第 \(2\) 行、矩阵 \(3\) 中的第 \(1\) 行。也就是矩阵 \(1\) 中的第 \(1\) 、 \(4\) 、 \(5\) 行
在求解这个问题的过程中,我们第 \(1\) 步选择第 \(1\) 行是正确的,但是不是每个题目第 \(1\) 步选择都是正确的,如果选择第 \(1\) 行无法求解出结果出来,那么就要推倒之前的选择,从选择第 \(2\) 行开始,以此类推
从上面的求解过程来看,实际上求解过程可以如下表示
1、从矩阵中选择一行
2、根据定义,标示矩阵中其他行的元素
3、删除相关行和列的元素,得到新矩阵
4、如果新矩阵是空矩阵,并且之前的一行都是 \(1\),那么求解结束,跳转到6;新矩阵不是空矩阵,继续求解,跳转到1;新矩阵是空矩阵,之前的一行中有 \(0\),跳转到5
5、说明之前的选择有误,回溯到之前的一个矩阵,跳转到1;如果没有矩阵可以回溯,说明该问题无解,跳转到7
6、求解结束,把结果输出
7、求解结束,输出无解消息
相关题目
Luogu P4929 【模板】舞蹈链(DLX)
原题链接
思路
咕咕咕
Luogu P1074 [NOIP2009 提高组] 靶形数独
原题链接
思路
咕咕咕
Luogu P4205 [NOI2005] 智慧珠游戏
原题链接
思路
咕咕咕
参考内容
标签:选择,求解,矩阵,标示,笔记,学习,一行,跳转,DLX 来源: https://www.cnblogs.com/syqwq/p/16206811.html