首页 > 其他分享> > SP12005 GRASSPLA - Grass Planting 题解

SP12005 GRASSPLA - Grass Planting 题解

2022-04-20 20:31:59 作者：互联网

题目传送门

更好的阅读体验

Solution I

这几乎是一道树链剖分模板题，和模板题唯一的区别在于这题维护的是边权。

因为除了根以外的节点都有父亲，但是叶子数量很多，所以我们让深度大的节点存储边的信息，就方便处理很多了。

在操作的时候，因为深度大的节点存储的才是边的信息，所以最顶端的节点是不能计算的。

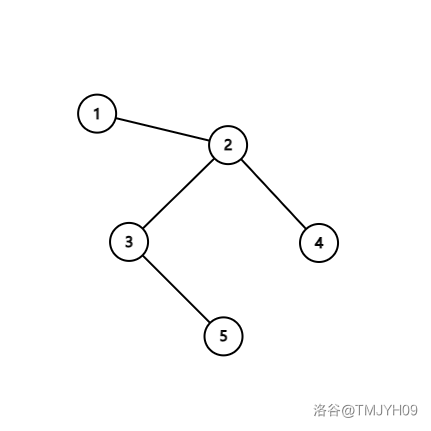
如图，若操作 \([2,5]\)，那么操作到最后（处于同一条重链上），就得操作顶端节点的重儿子。

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

const int N = 1e5+10;
int n,m;
struct edge{
    int to,nxt;
}e[N<<1];
int head[N],idx;
void add(int x,int y){
    e[++idx]={y,head[x]};
    head[x]=idx;
}

int fa[N],son[N],dep[N],siz[N],top[N];
int seg[N],dfn;
void dfs1(int u,int f,int depth){
    fa[u]=f;dep[u]=depth;siz[u]=1;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v!=f){
            dfs1(v,u,depth+1);
            siz[u]+=siz[v];
            if(siz[v]>siz[son[u]])son[u]=v;
        }
    }
}
void dfs2(int u,int tp){
    top[u]=tp;
    seg[u]=++dfn;
    if(!son[u])return;
    dfs2(son[u],tp);
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(!seg[v]){
            dfs2(v,v);
        }
    }
}
struct segment{
    int l,r;
    int sum,add;
}tr[N<<4];
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
inline void pushup(int p){tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;}
void build(int p,int l,int r){
    tr[p].l=l;tr[p].r=r;
    if(l==r)return;
    int mid=l+r>>1;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    pushup(p);
}
void pushdown(int p){
    if(tr[p].add){
        tr[ls(p)].add+=tr[p].add;
        tr[rs(p)].add+=tr[p].add;
        tr[ls(p)].sum+=(tr[ls(p)].r-tr[ls(p)].l+1)*tr[p].add;
        tr[rs(p)].sum+=(tr[rs(p)].r-tr[rs(p)].l+1)*tr[p].add;
        tr[p].add=0;
    }
}
void tr_add(int p,int l,int r,int k){
    if(l<=tr[p].l&&tr[p].r<=r){
        tr[p].add+=k;tr[p].sum+=(tr[p].r-tr[p].l+1)*k;
        return;
    }
    pushdown(p);
    int mid=tr[p].l+tr[p].r>>1;
    if(l<=mid)tr_add(ls(p),l,r,k);
    if(mid<r)tr_add(rs(p),l,r,k);
    pushup(p);
}
int tr_query(int p,int l,int r){
    if(l<=tr[p].l&&tr[p].r<=r)return tr[p].sum;
    pushdown(p);
    int mid=tr[p].l+tr[p].r>>1;
    int ans=0;
    if(l<=mid)ans+=tr_query(ls(p),l,r);
    if(mid<r)ans+=tr_query(rs(p),l,r);
    return ans;
}
void seg_add(int x,int y,int k){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        tr_add(1,seg[top[x]],seg[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    tr_add(1,seg[x]+1,seg[y],k);
}
int seg_query(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        ans+=tr_query(1,seg[top[x]],seg[x]);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    ans+=tr_query(1,seg[x]+1,seg[y]);
    return ans;
}


int main(){
    ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
    cin>>n>>m;
    for(int i=1,x,y;i<n;i++){
        cin>>x>>y;
        add(x,y);add(y,x);
    }
    dfs1(1,0,1);
    dfs2(1,1);
    build(1,1,n);
    while(m--){
        char op;int x,y;
        cin>>op>>x>>y;
        if(op=='P'){
            seg_add(x,y,1);
        }if(op=='Q'){
            cout<<seg_query(x,y)<<endl;
        }
    }
    return 0;
}

Solution II

维护树上问题还有一种更加强大的数据结构，就是 Link Cut Tree，简称 LCT。

当然这题用 LCT 来做简直是降维打击，LCT 的更多精彩操作请前往模板题。

跟树链剖分一样，LCT 通常维护点权，该如何维护边权呢？

由于 LCT 是由动态的 splay 维护，父亲及儿子会因为旋转不停改变，所以不能像树剖那样存储在深度大的节点。

解决方案是建虚节点，第 \(i\) 条边的权值存储在 \(i+n\) 个节点，连接 \(x\rightarrow y\) 这条边就是连接 \(x\rightarrow i+n\)，再连接 \(i+n\rightarrow y\)。至于 \(x\) 和 \(y\) 节点直接赋值 \(0\) 就行了。

由于维护了边权，pushup() 和 pushdown() 需要判断 \(x\) 是边（虚节点）还是普通节点。

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

const int N = 1e6 + 10;
int n,m;
struct lct{
    int son[2],fa,val,siz,sum;
    int add,rev;
}tr[N<<2];
#define ls(x) (tr[x].son[0])
#define rs(x) (tr[x].son[1])
#define fa(x) (tr[x].fa)
inline void pushup(int x){
    tr[x].siz=tr[ls(x)].siz+tr[rs(x)].siz+x>n?1:0;
    tr[x].sum=tr[ls(x)].sum+tr[rs(x)].sum+tr[x].val;
}
inline bool isroot(int x){return !(ls(fa(x))==x || rs(fa(x))==x);}
inline void reverse(int x){swap(ls(x),rs(x));tr[x].rev^=1;}
inline void add(int x,int k){
    if(x>n){
        tr[x].val+=k;tr[x].sum+=tr[x].siz*k;
    }
    tr[x].add+=k;
}
void pushdown(int x){
    if(tr[x].add){
        if(ls(x))add(ls(x),tr[x].add);
        if(rs(x))add(rs(x),tr[x].add);
        tr[x].add=0;
    }
    if(tr[x].rev){
        if(ls(x))reverse(ls(x));
        if(rs(x))reverse(rs(x));
        tr[x].rev=0;
    }
}
void pushall(int x){
    if(!isroot(x))pushall(fa(x));
    pushdown(x);
}
void rotate(int x){
    int y=fa(x),z=fa(y);
    int k=rs(y)==x;
    if(!isroot(y))tr[z].son[rs(z)==y]=x;
    fa(x)=z;
    tr[y].son[k]=tr[x].son[k^1],fa(tr[x].son[k^1])=y;
    tr[x].son[k^1]=y,fa(y)=x;
    pushup(y);pushup(x);
}
void splay(int x){
    pushall(x);
    while(!isroot(x)){
        int y=fa(x),z=fa(y);
        if(!isroot(y)){
            if((rs(z)==y) ^ (rs(y)==x))rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
}
void access(int x){
    for(int y=0;x;x=fa(y=x)){
        splay(x);rs(x)=y;pushup(x);
    }
}
void makeroot(int x){
    access(x);splay(x);reverse(x);
}
int findroot(int x){
    access(x);splay(x);
    while(ls(x)){
        pushdown(x);
        x=ls(x);
    }
    splay(x);
    return x;
}
void link(int x,int y){
    makeroot(x);
    if(findroot(y)==x)return;
    fa(x)=y;
}
void split(int x,int y){
    makeroot(x);access(y);splay(y);
}

int main(){
    ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
    cin>>n>>m;
    for(int i=1,x,y;i<n;i++){
        cin>>x>>y;
        tr[i+n].siz=1;
        link(x,i+n);link(i+n,y);
    }
    while(m--){
        char p;int a,b;
        cin>>p>>a>>b;
        if(p=='P'){
            split(a,b);add(b,1);
        }else{
            split(a,b);cout<<tr[b].sum<<endl;
        }
    }
    return 0;
}

时空对比

树链剖分

Link Cut Tree

可以发现，树链剖分的时间复杂度是优于 LCT 的（线段树快过 splay），但是在空间上以及码量上，LCT 都胜过树剖。

标签：Planting,rs,int,题解,tr,fa,add,ls,Grass
来源： https://www.cnblogs.com/tmjyh09/p/16171589.html