首页 > 其他分享> > 机器学习性能指标

机器学习性能指标

2022-04-18 16:33:23 作者：互联网

一、混淆矩阵

混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目：第一行第一列中的43表示有43个实际归属第一类的实例被预测为第一类，同理，第一行第二列的2表示有2个实际归属为第一类的实例被错误预测为第二类。

如有150个样本数据，预测为1,2,3类各为50个。分类结束后得到的混淆矩阵为：

	预测
类1	类2	类3
实际	类1	43	2	0
类2	5	45	1
类3	2	3	49

每一行之和表示该类别的真实样本数量，每一列之和表示被预测为该类别的样本数量，

第一行说明有43个属于第一类的样本被正确预测为了第一类，有两个属于第一类的样本被错误预测为了第二类。

True Positive(真正, TP)：将正类预测为正类数.

True Negative(真负 , TN)：将负类预测为负类数.

False Positive(假正, FP)：将负类预测为正类数 $\rightarrow$ 误报 (Type I error).

False Negative(假负 , FN)：将正类预测为负类数 $\rightarrow$ 漏报 (Type II error).

以下信息来自：

https://www.zhihu.com/question/19645541/answer/91694636

精确率(precision)和准确率(accuracy)是不一样的。

一.定义辨析

刚开始接触这两个概念的时候总搞混，时间一长就记不清了。

实际上非常简单，精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了，一种就是把正类预测为正类(TP)，另一种就是把负类预测为正类(FP)，也就是
$P = \frac{TP}{TP+FP}$
而召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN)。
$R = \frac{TP}{TP+FN}$

其实就是分母不同，一个分母是预测为正的样本数，另一个是原来样本中所有的正样本数。

在信息检索领域，精确率和召回率又被称为查准率和查全率，

查准率＝检索出的相关信息量 / 检索出的信息总量

查全率＝检索出的相关信息量 / 系统中的相关信息总量

二.举个栗子

假设我们手上有60个正样本，40个负样本，我们要找出所有的正样本，系统查找出50个，其中只有40个是真正的正样本，计算上述各指标。

TP: 将正类预测为正类数 40
FN: 将正类预测为负类数 20
FP: 将负类预测为正类数 10
TN: 将负类预测为负类数 30

准确率(accuracy) = 预测对的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%

精确率(precision) = TP/(TP+FP) = 80%

召回率(recall) = TP/(TP+FN) = 2/3

二、ROC曲线

定义：

In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied

比如在逻辑回归里面，我们会设一个阈值，大于这个值的为正类，小于这个值为负类。如果我们减小这个阀值，那么更多的样本会被识别为正类。这会提高正类的识别率，但同时也会使得更多的负类被错误识别为正类。为了形象化这一变化，在此引入 ROC ，ROC 曲线可以用于评价一个分类器好坏。

ROC 关注两个指标，直观上，TPR 代表能将正例分对的概率，FPR 代表将负例错分为正例的概率。在 ROC 空间中，每个点的横坐标是 FPR，纵坐标是 TPR，这也就描绘了分类器在 TP（真正率）和 FP（假正率）间的 trade-off。

解释：

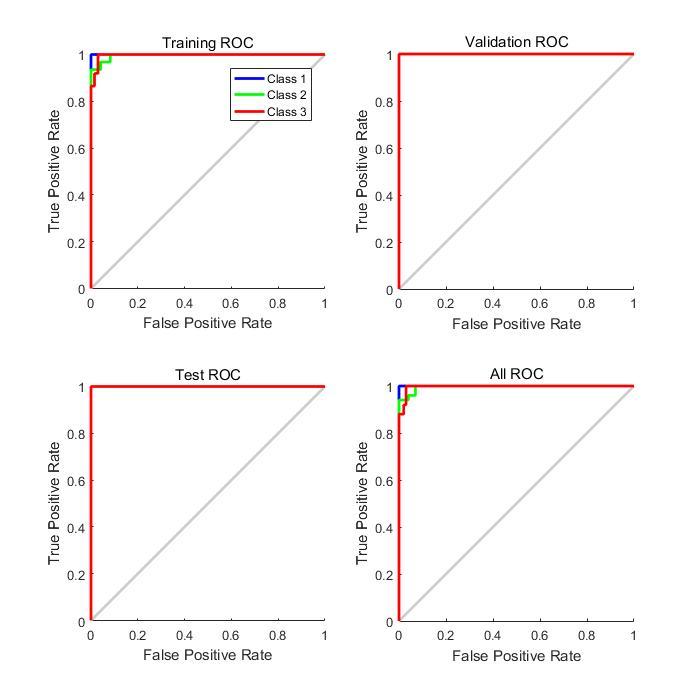
ROC曲线简介

通过ROC空间，我们明白了一条ROC曲线其实代表了无数个分类器。那么我们为什么常常用一条ROC曲线来描述一个分类器呢？仔细观察ROC曲线，发现其都是上升的曲线（斜率大于0），且都通过点（0,0）和点（1,1）。其实，这些点代表着一个分类器在不同阈值下的分类效果，具体的，曲线从左往右可以认为是阈值从0到1的变化过程。当分类器阈值为0，代表不加以识别全部判断为0，此时TP=FP=0，TPR=TP/P=0，FPR=FR/N=0；当分类器阈值为1，代表不加以识别全部判断为1，此时FN=TN=0，P=TP+FN=TP, TPR=TP/P=1，N=FP+TN=FP, FPR=FR/N=1。所以，ROC曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。

AUC曲线

定义：

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。

The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.

翻译过来就是，随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。

简单说：AUC值越大的分类器，正确率越高3。

$AUC = 1$，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
$0.5 < AUC < 1$，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
$AUC = 0.5$，跟随机猜测一样（例：丢铜板），模型没有预测价值。
$AUC < 0.5$，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在 $AUC < 0.5$ 的情况。

AUC面积为0.5为随机分类，识别能力为0，面积越接近于1识别能力越强，面积等于1为完全识别。

三、回归

平均绝对误差

平均绝对误差MAE（Mean Absolute Error）又被称为 $l_1$ 范数损失（l1-norm loss）：

平均平方误差

平均平方误差 MSE（Mean Squared Error）又被称为 $l_2$ 范数损失（l2-norm loss）：

标签：分类器,ROC,机器,预测,样本,TP,学习,正类,性能指标
来源： https://www.cnblogs.com/limbercode/p/16160242.html