CF930C Teodor is not a liar! 结论

看了看没有人写详细的证明……可能觉得太简单了？

另外，我不觉得题面上的翻译是给人类阅读的……

万老爷翻的题意：

Teodor 有 \(n\) 条线段,端点都是正整数且在 \([1,m]\) 之间.他发现 没有一个整点满足在所有线段上。他把这个事实告诉 Sasha 然而她不信. Sasha 可以向 Teodor 询问若干个整点 \(x_i\) ,Teodor会回答 \(cnt(x_i)\) 表示 \(x_i\) 在多少条线段上.

提醒：Sasha 不知道 \(n\) 的大小。Sasha 很聪明，所以 \(x_i\) 互不相同。

\(cnt_x\) : 整数点 \(x\) 出现在 \(cnt_x\) 条线段上（题面中的定义），可以 \(O(n)\) 差分预处理。

所有整数点都不同时存在于所有线段上 其实就说明有至少两条线段不相交。不相交那就有一个点在“分界“上。那么或许 【能证明某点是分界点】 就说明有 【至少两条线段不相交】？

我们有结论：能判断出所有整数点都不同时存在于所有线段上 \(\Leftrightarrow \exists x_1<x_2<x_3\)，满足 \(cnt_{x_2}<cnt_{x_1},cnt_{x_2}<cnt_{x,3}\)

Proof

必要性：

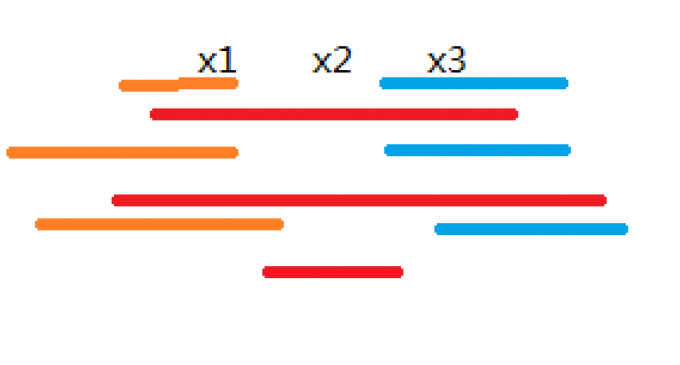
有至多 \(cnt_{x_2}\) 条线段（红色）同时经过 \(x_1,x_3\)，那么还有 \(cnt_{x_1}-cnt_{x_2}\) 条（橙色）无法到达 \(x_2\)，\(cnt_{x_3}-cnt_{x_2}\) 条（蓝色）无法到达 \(x_2\)，那么 \(x_2\) 就成为了橙色和蓝色的分界线，每个整数点会“属于”橙色 或 “属于”蓝色 或 都不属于。

充分性：
如果当前还没有问出来这么一个 \(x_2\)，那么根据当前问出来的信息，是一个单峰的序列，肯定能构造出一种 【存在一个整数点同时存在于所有线段上】 的情况。（例如一层层叠上去，峰点会存在于所有线段上）

那么我们不能满足这一条件的最大问题数，其实就是 单峰的最长序列。

树状数组正着和反着求两遍最长上升子序列即可。

虽然但是，这种结论到底是怎么想出来的啊/ll

标签：cnt,liar,线段,所有,整数,Sasha,Teodor,CF930C
来源： https://www.cnblogs.com/zdsrs060330/p/16151793.html