首页 > 其他分享> > 【Black-Panda】LCA最近公共祖先学习笔记

【Black-Panda】LCA最近公共祖先学习笔记

2022-04-05 18:00:58 作者：互联网

1. 定义：

LCA（Least Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点 \(x\) 和 \(y\) 最近的公共祖先（深度最大的祖先），记为：\(LCA(x,y)\)。

举例：

\(LCA(15,12)=4\)
\(LCA(10,12)=10\)

图例：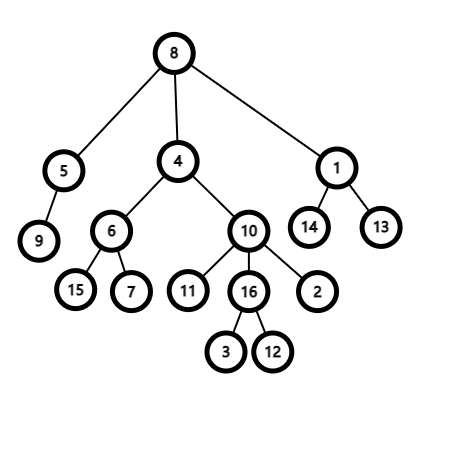

作用：能在 \(log(n)\) 解决从 \(u\) 到 \(v\) 的路线问题。

2. 求解：

方法一：向上标记法（暴力求解）

从 \(x\) 向上走到根节点，并标记所有走过的结点。
从 \(y\) 走到根，当第一次遇到有标记的结点时，就找到了 \(LCA(x,y)\)。
最坏时间 \(O(n)\)。
给出代码片段：

int LCA(int x,int y){
	while(x>0)vis[x]=1,x=fa[x];
	while(y>0 && !vis[y])y=fa[y];
	return y;
}

方法二：暴力优化

用 \(fa[i]\) 记录 \(i\) 的父亲结点。
首先将 \(x\) 和 \(y\) 中深度较深的那个点跳到和较浅的点同样的深度。
然后两个点一起一步一步向上跳，直到跳到同一个点 \(p\)，就是它们的 \(LCA\)。
复杂度：最坏情况 \(O(o)\)，适合只计算一次 \(LCA(x,y)\)。

\(p=LCA(x,y)\)
结点深度：\(d[x],d[y]\)
\(x\) 向上走 \(d[x]-d[p]\)

\(y\) 向上走 \(d[y]-d[p]\)
实现方法：\(u\) 和 \(v\) 深度大的向上走 \(|d[x]-d[y]|\)，再一起一步一步向上走，直到走到同一个结点 \(p\)。
时间：\(O(d[x]+d[y])\)
存储：有向图的邻接表

vector<int> G[maxn];
int fa[maxn];
int d[maxn];

深度优先遍历，同时求 \(fa[]\)

\(dfs(root,1);\)

void dfs(int u,int depth){
	d[u]=depth;
	int m=G[u].size();
	for(int i=0;i<m;i++){
		int v=G[u][i];
		dfs(v,depth+1);
	}
}

参考代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;

vector<int> G[maxn];
int fa[maxn],d[maxn],n,m,s;

void dfs(int u,int p,int depth){
	d[u]=depth;
	fa[u]=p;
	for(int i=0;i<G[u].size();i++){
		int v=G[u][i];
		if(v!=p)	dfs(v,u,depth+1);
	}
}

int LCA(int x,int y){
	while(d[x]>d[y])	x=fa[x];
	while(d[x]<d[y])	y=fa[y];
	while(x!=y){
		x=fa[x];y=fa[y];
	}
	return x;
}

int main(){
	scanf("%d%d%d",&n,&m,&s);
	int u,v;
	for(int i=1;i<n;i++){
		scanf("%d%d",&u,&v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs(s,-1,1);
	for(int i=0;i<m;i++){
		scanf("%d%d",&u,&v);
		printf("%d\n",LCA(u,v));
	}
	return 0;
}

方法三：二进制拆分思想（倍增）

求 \(LCA(x,y)\) 的步骤：

设 \(d[x]\) 表示 \(x\) 的深度。假设 \(d[x]>=d[y]\) （否则可以交换 \(x\) 和 \(y\)）。
利用二进制拆分思想，把 \(x\) 向上调整到 \(y\) 同一高度。
\(x\) 向上走 \(i=2^{log_n},...,2^1,2^0\) 步，检查 \(x\) 到达的节点是否比 \(y\) 深，若是则 \(x=fa[x][i]\)。
如果 \(x=y\)，\(LCA(x,y)=y\)。
利用二进制思想，\(x\) 和 \(y\) 同时往上跳，并保持深度一致且二者\(\color{#ff0000}{\text{不相遇}}\)。
\(x\) 和 \(y\) 同时向上走 \(i=2^{log_n},...,2^1,2^0\) 步。
如果 \(fa[x][i]!=fa[y][i]\)，则 \(x=fa[x][i],y=fa[y][i]\)。
此时只差一步就得相遇了，它们的父亲节点 \(fa[x][0]\)（或\(fa[y][0]\)），就是 \(LCA(x,y)\)。

3.推荐

bilibili:BV1nE411L7rz

标签：结点,int,fa,maxn,LCA,Black,向上,Panda
来源： https://www.cnblogs.com/liu-black/p/lca-biji.html

【Black-Panda】LCA最近公共祖先 学习笔记