卷积

理解卷积公式（狭隘）

\[\int_{-\infty}^{\infty} f(\tau) g(x-\tau) \mathrm{d} \tau \]

一个人24小时不间断进食，且一直在消化，消化的速率和他吃的东西没有关系。问下午两点这个人胃里还剩多少食物。

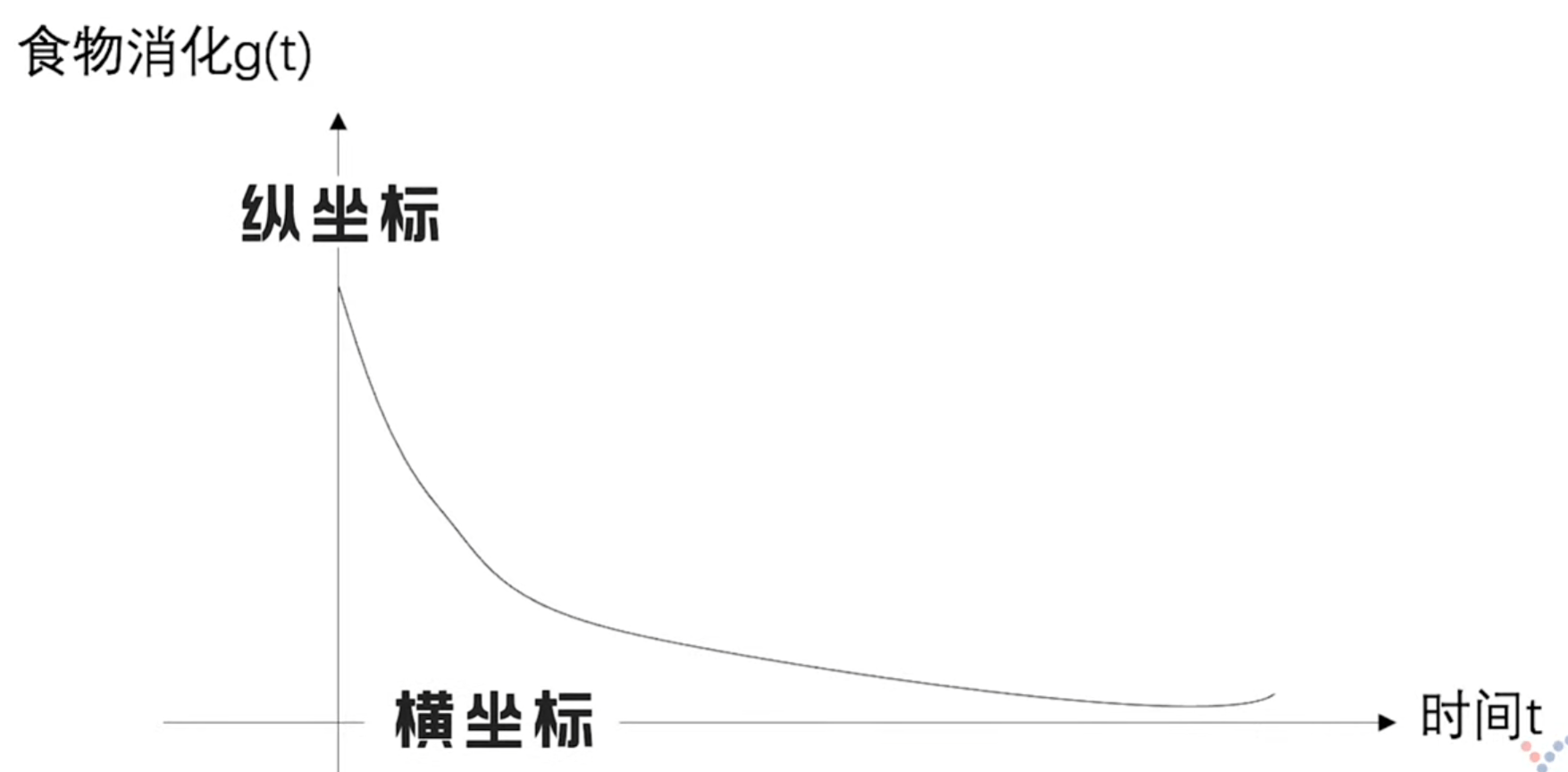
用f函数表示进食，用\(g\)函数表示消化，就能把下午两点这个人胃里还剩多少食物求解出来。

假设我们不考虑消化问题，那么就是对f函数的简单积分。但是引入消化，只看f函数就不够了。

比如中午12点吃了一碗米饭。那么到下午两点米饭在胃里还剩余 \(f(12) \cdot g(14-12)\)，其他食物同理。

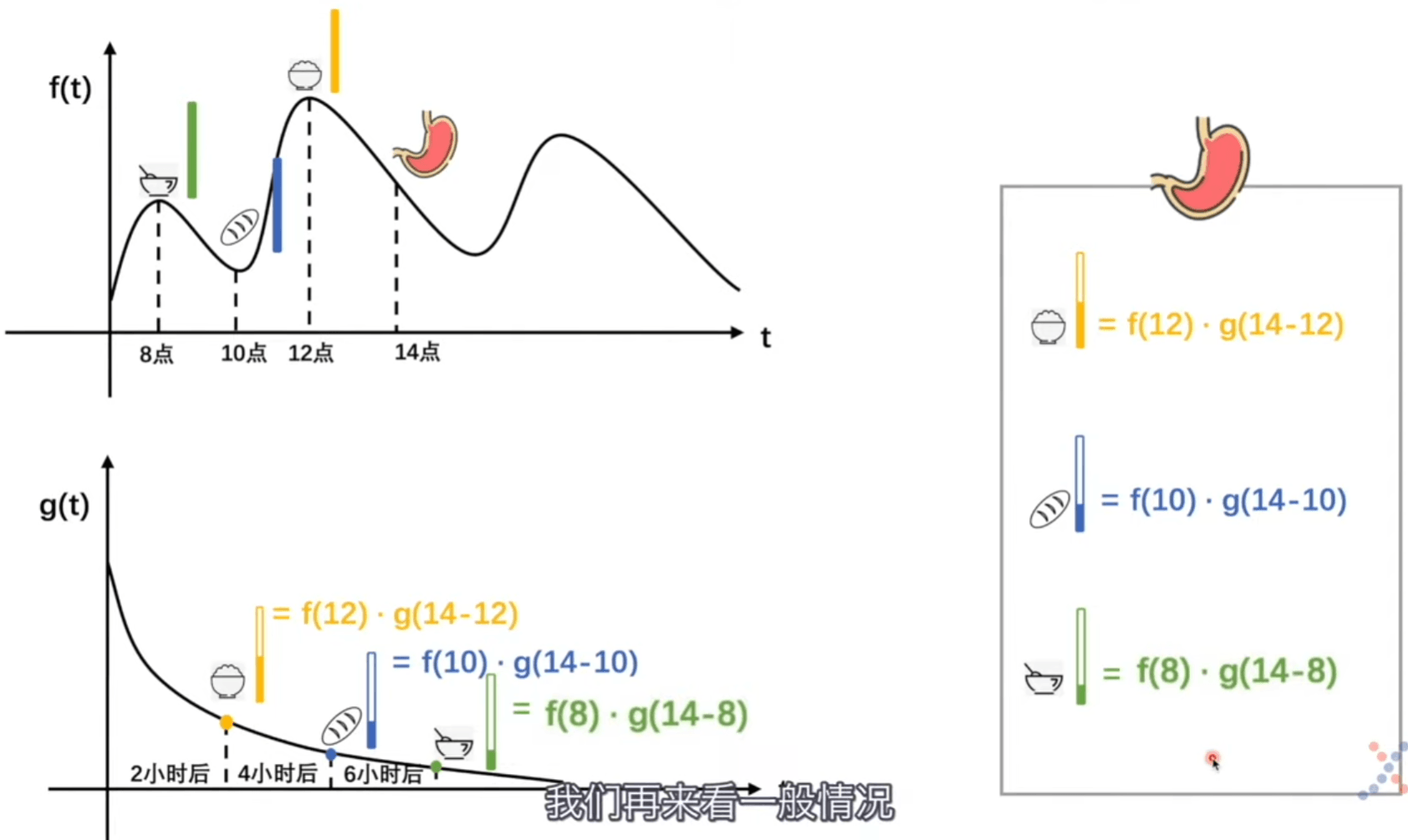
这是考虑特殊情况（单独食物），现在我们考虑一般情况（所有食物）。

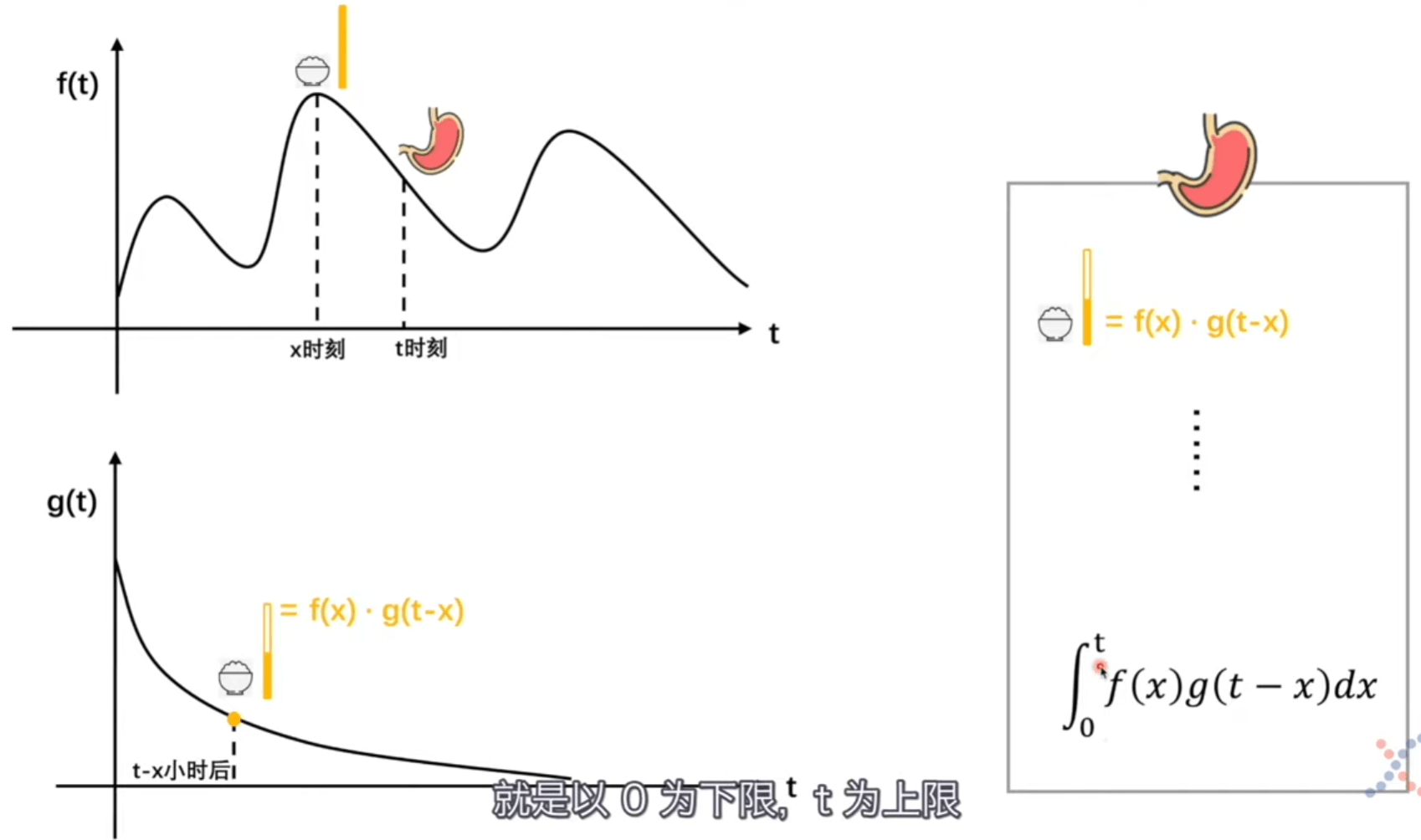
关注 \(x 、t-x\) 两个变量，两个变量相加后会消掉其中一个。

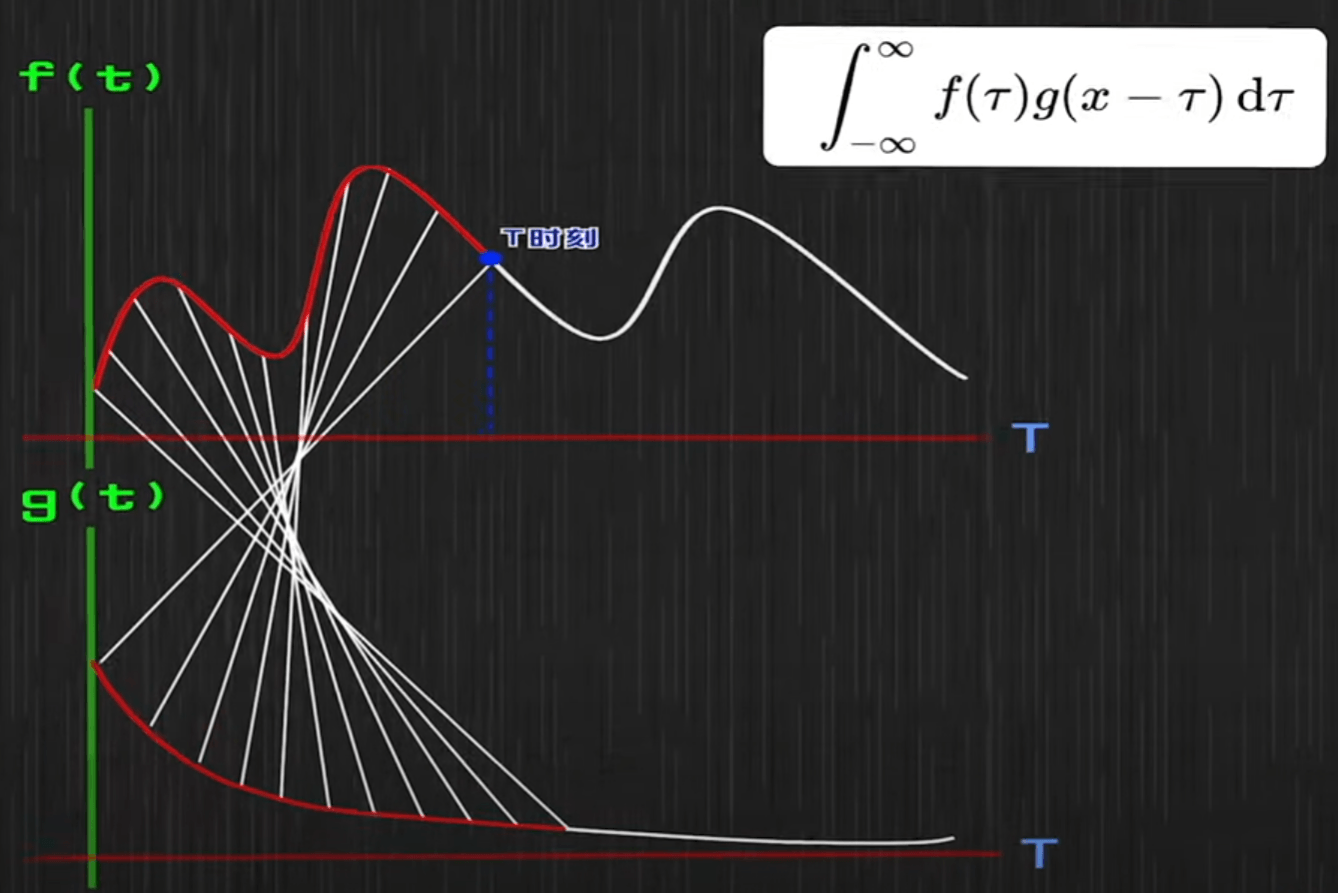
\(x、t-x\) 对应的是f函数到g函数的一条连线。每一对连线都是 \(f(x)\) 和 \(g(t-x)\)，我们把它相加起来。

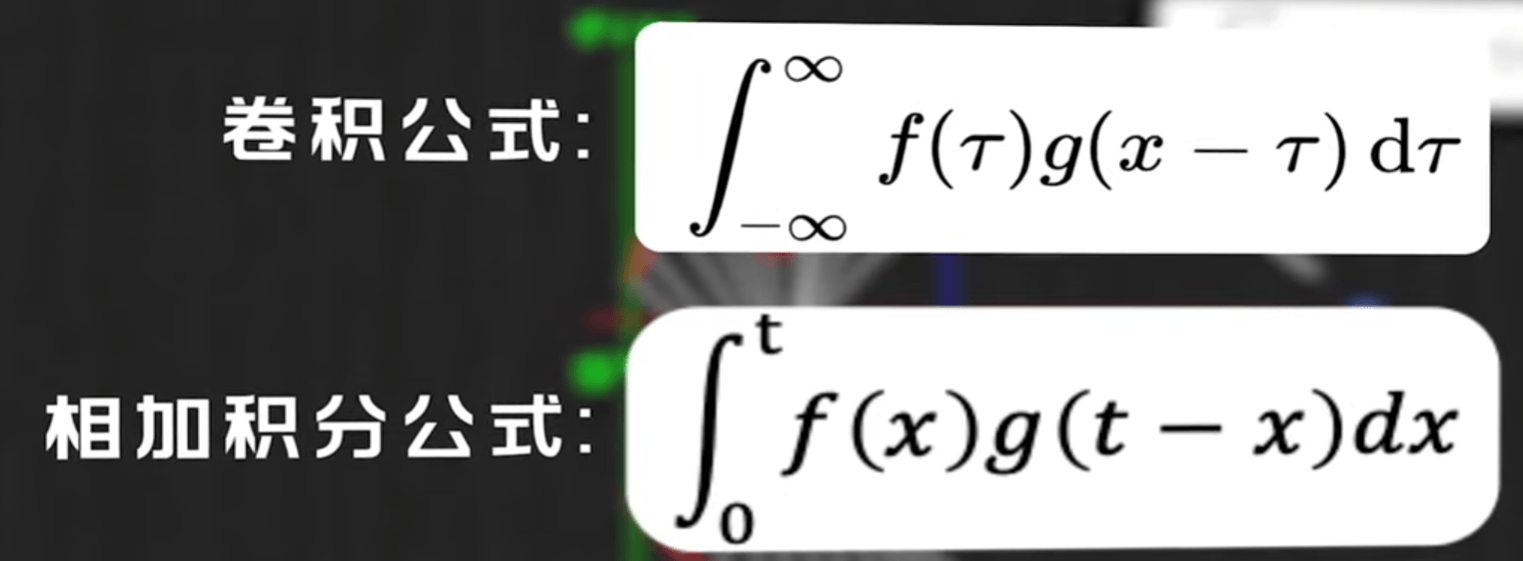
我们这里引入了时间，是具有物理意义的。所以不能负无穷，像距离就可以负无穷了。

卷积的物理意义

• 一个系统
• 输入不稳定
• 输出稳定
• 用卷积求系统存量

为什么叫卷积（狭隘）

把g函数翻转一下，所以叫卷积

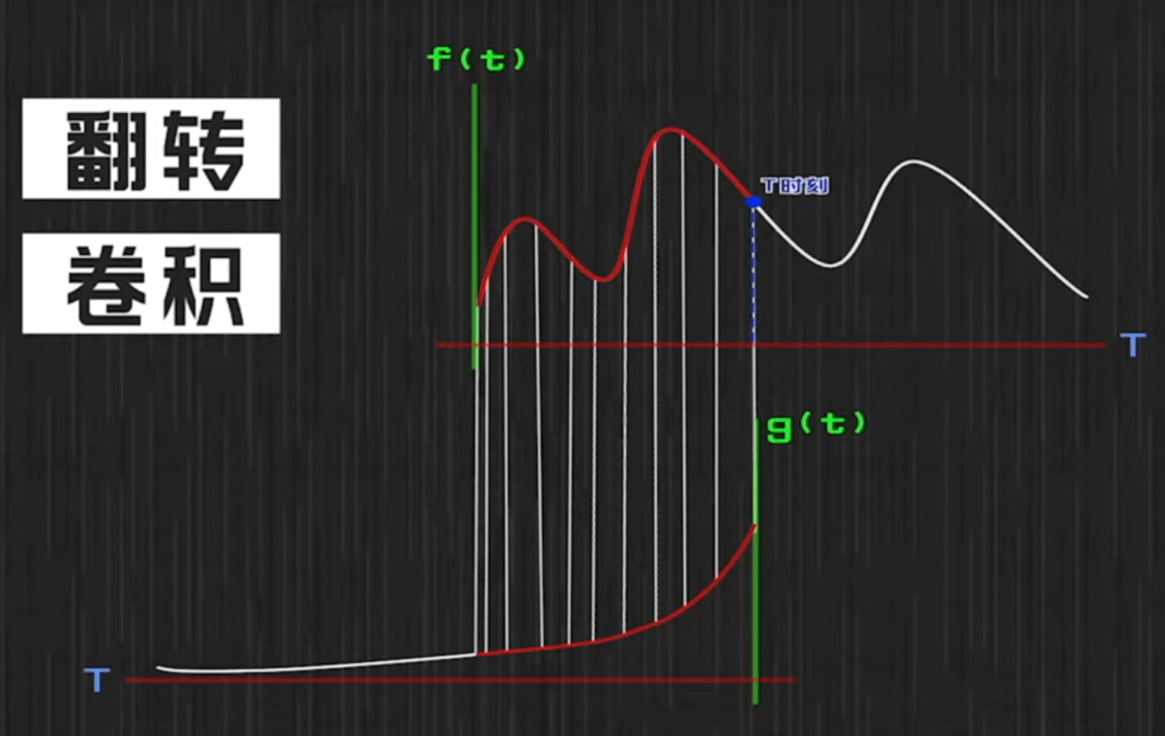
图像的卷积操作

从前面的例子，卷积操作无非就是 f、g两个函数。所以我们要去找图像卷积操作两个f、g的函数。

f函数就是不稳定输入，g函数就是稳定输出。

电脑里的图片可以看做是一个个像素点组成的，具有灰度值，rgb值等信息。

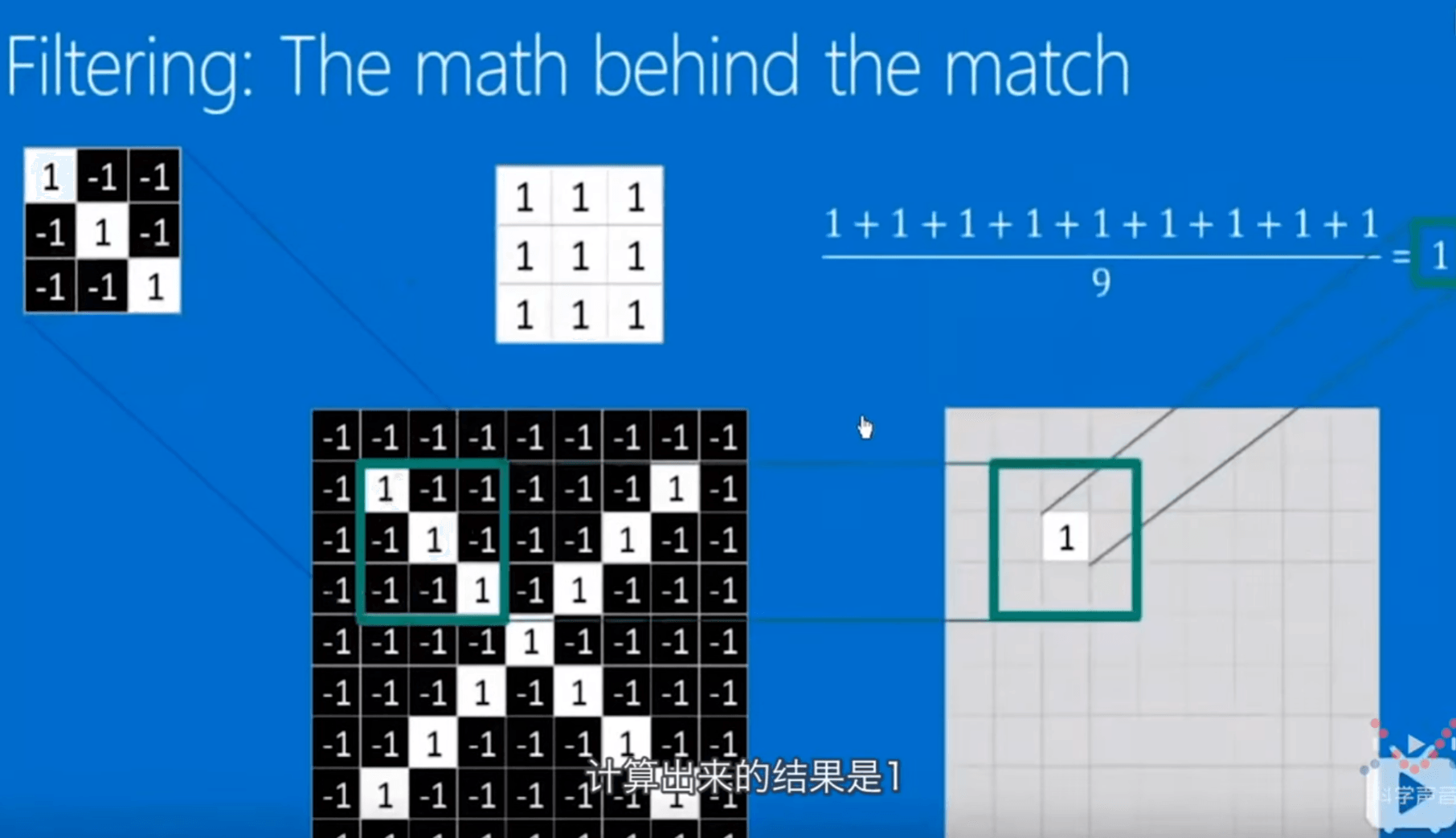
卷积操作就是用 3*3 的点阵（卷积核）和图像进行一个操作，将卷积核扣在图像的点阵上。对应的两个格子相乘。将相乘的九个结果相加保存对应到一个新像素值。用卷积核把整个图像都扫一遍，图像外围加一层0像素边使边缘像素点也能被计算。

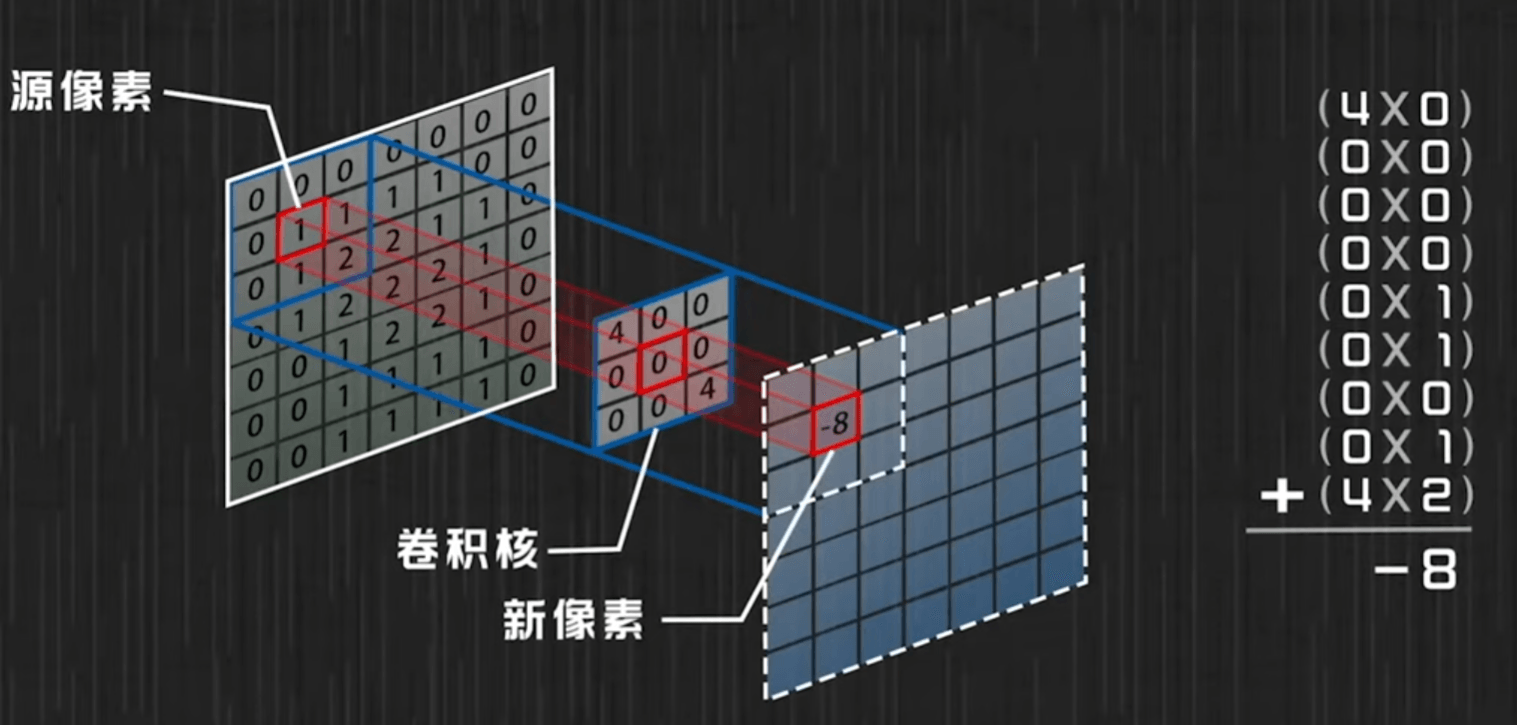
图像的卷积操作就是拿图片和卷积核先相乘再相加。直觉上看。图像和卷积核一个应该是f，一个应该是g。

图像里的像素点总在变化对应系统不稳定的输入，而卷积核不变对应的是稳定的输出。

这里的问题跟之前的吃饭问题不一样，这里是一个二维问题，f函数应该是一个平面波。

卷积核和g函数有什么关系呢？我们需要改变对卷积的理解。一个图像不是系统，没有稳定输入也没有稳定输出。

再回到原来吃饭的例子，我们把吃东西看成系统的输入，消化看成系统的输出，胃里的存量是系统的存量，仅靠这个例子很难跳出去对他有一个更广泛的理解。所以我们换一个例子。

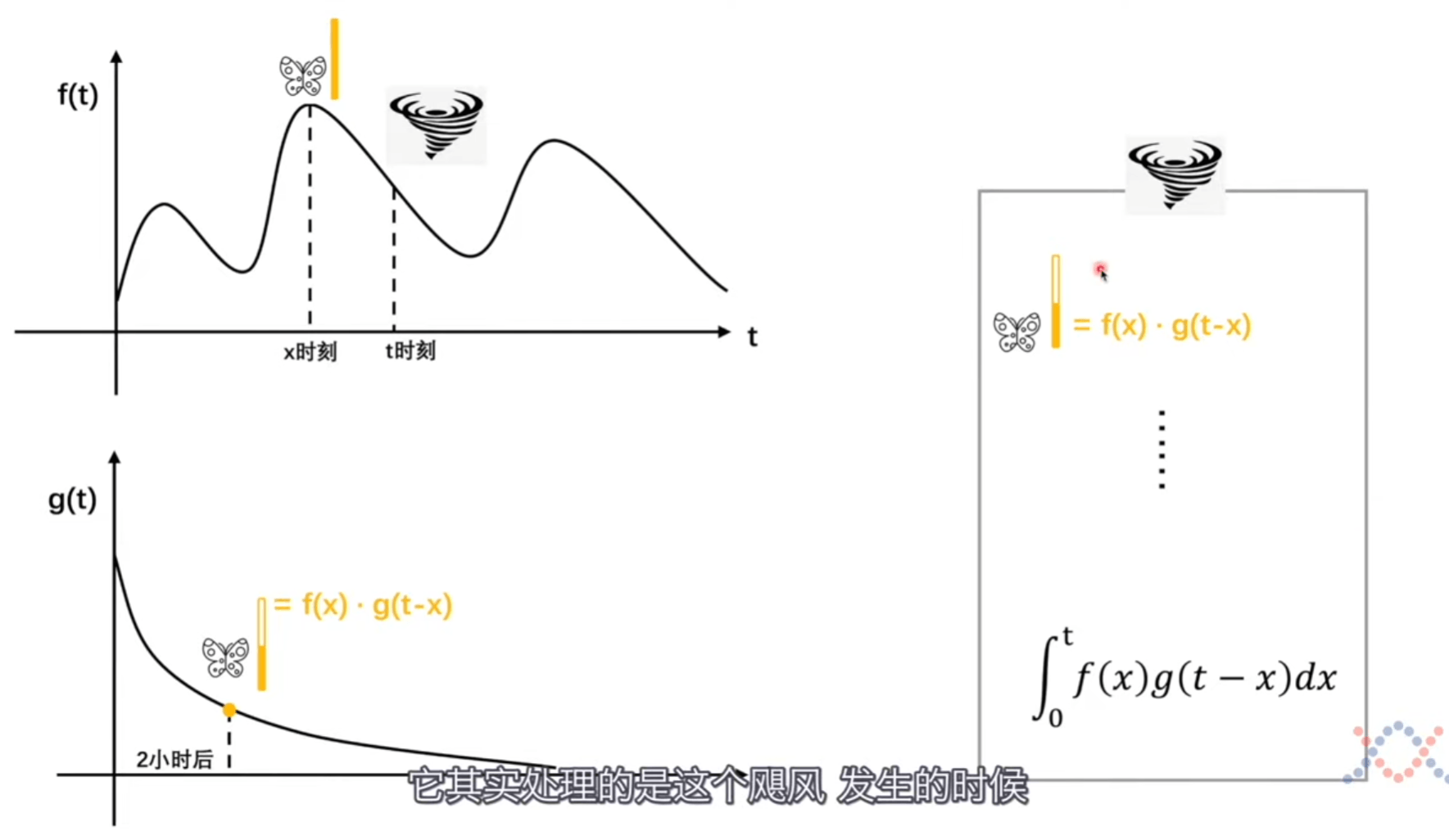
假如在t时刻发生飓风，原因是很多蝴蝶煽动翅膀。在x时刻对飓风产生影响，产生的影响力会随时间变化逐渐衰减。

我们可以这样理解卷积，在某一个时刻发生一件事，而这件事会受到之前很多事的影响，比如x时刻发生的一件事，会对t时刻产生影响，具体怎么影响要看x到t时刻经历的时间，规定随时间影响力变化的函数是g函数。我们也可以把视野放宽一点，不仅仅是时间，而是发生事件的位置等等。

平滑卷积操作

平滑就是让周围的像素点和自己相差不要太大。

卷积核就是周围像素点对当前像素点产生的影响。卷积核理论上可以无限大，由于我们这是计算机问题，要考虑性价比，所以就用 3*3 的点阵。

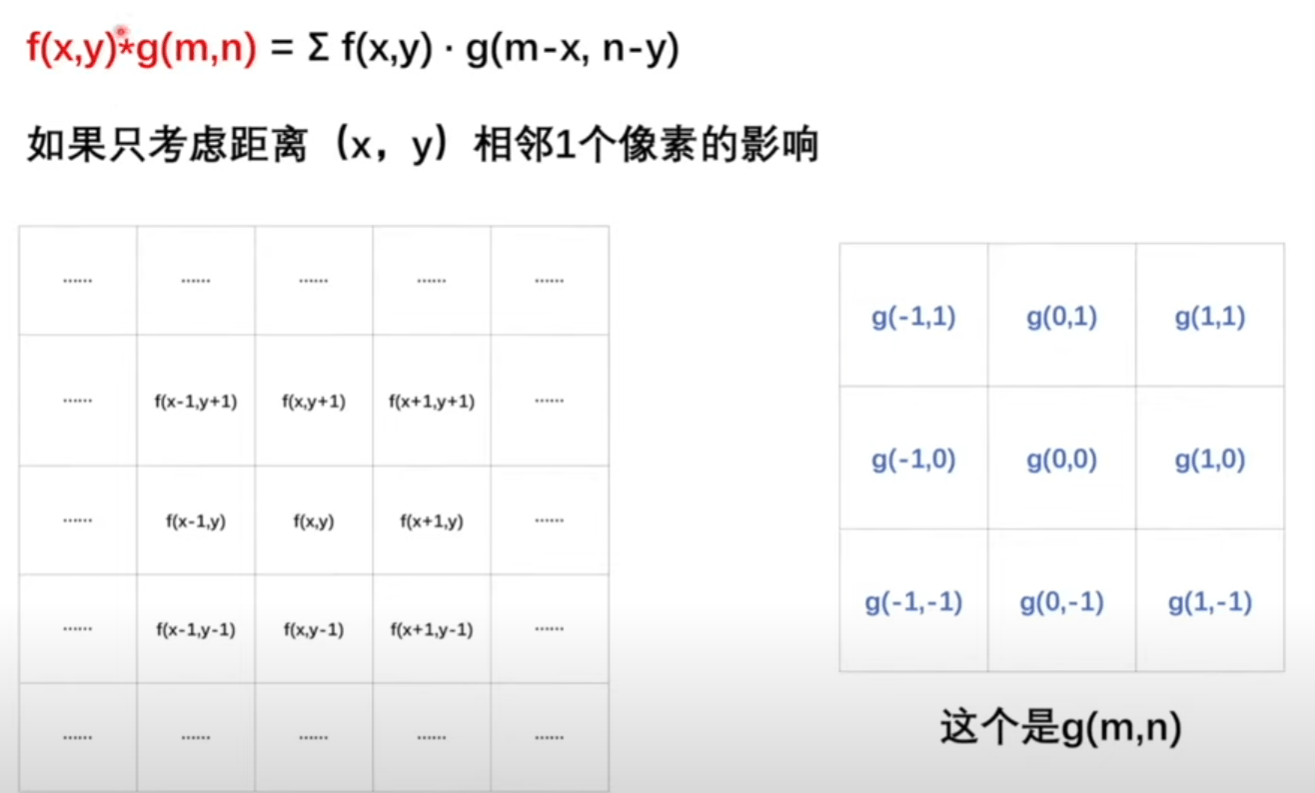
红色公式是进行卷积操作，后面参数相加消掉其中一项可以拿来判断是不是卷积的典型标志。

前面的求和符号因为考虑的是像素点，所以不是连续的，需要连加表示。

求一个像素点对另一个像素点产生了什么影响，我们使用类比法，可以把两个像素点看成不同时刻的事件。我们要考虑的就是t时刻之前所有的时间对t时刻发生的事情产生的影响。现在我们就是相当于在考虑周围像素点对中心像素点产生的影响。那么g函数里的参数是 \(t-x\)，同样可以类比计算 \(x-(x-1) = 1\) 、\(y-(y-1) = 1\)

将右侧g函数图像旋转180度，就可以清晰对应。

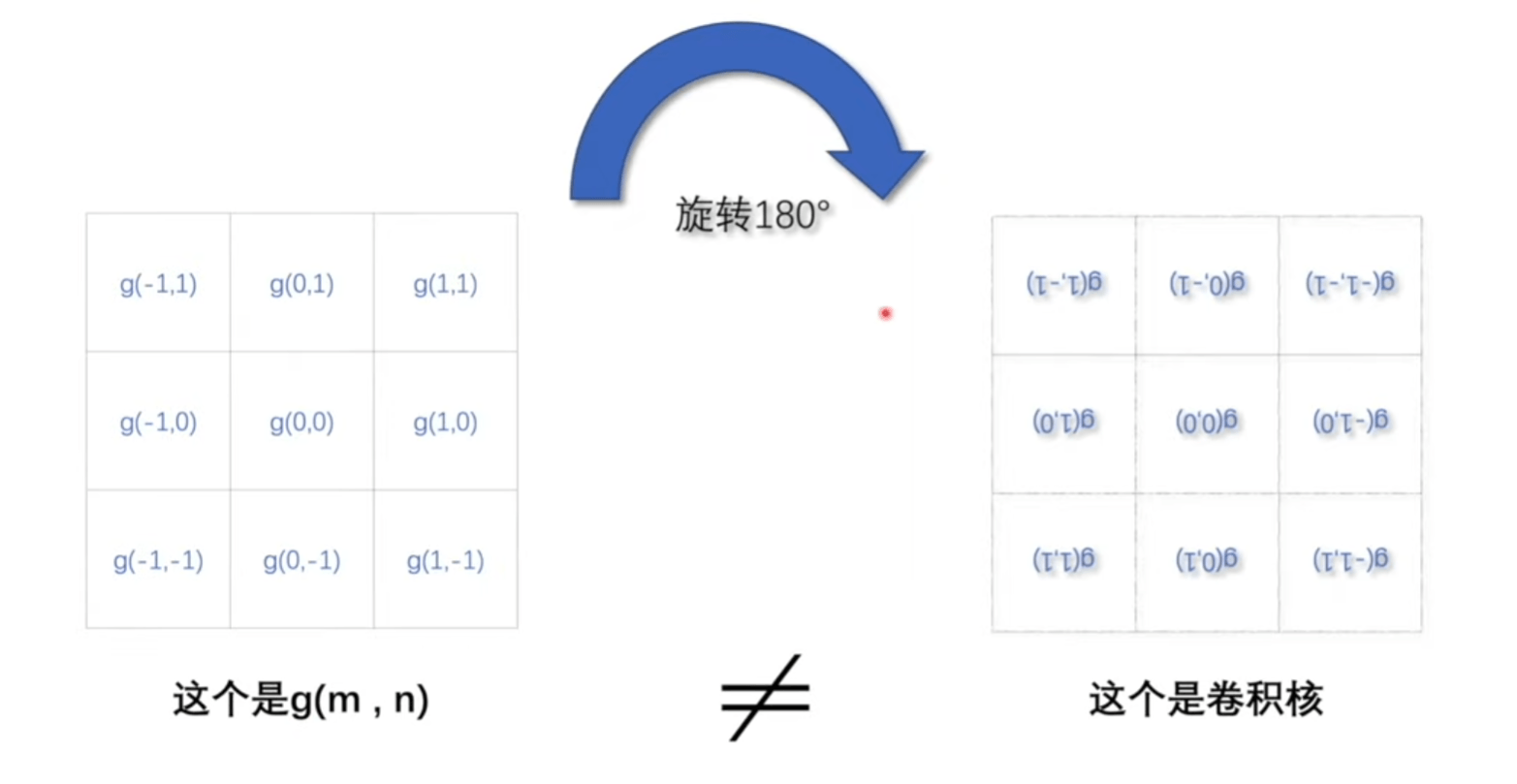
卷积核是可以直接扣在图像上进行卷积相加。

把卷积当做是周围像素点对当前像素点的影响，而g函数规定了如何影响的关键。

考虑图像的卷积操作不只能看平滑卷积核，卷积操作不只有平滑卷积核。

使用特定的卷积核可以挑出图片里的特征。

卷积神经网络

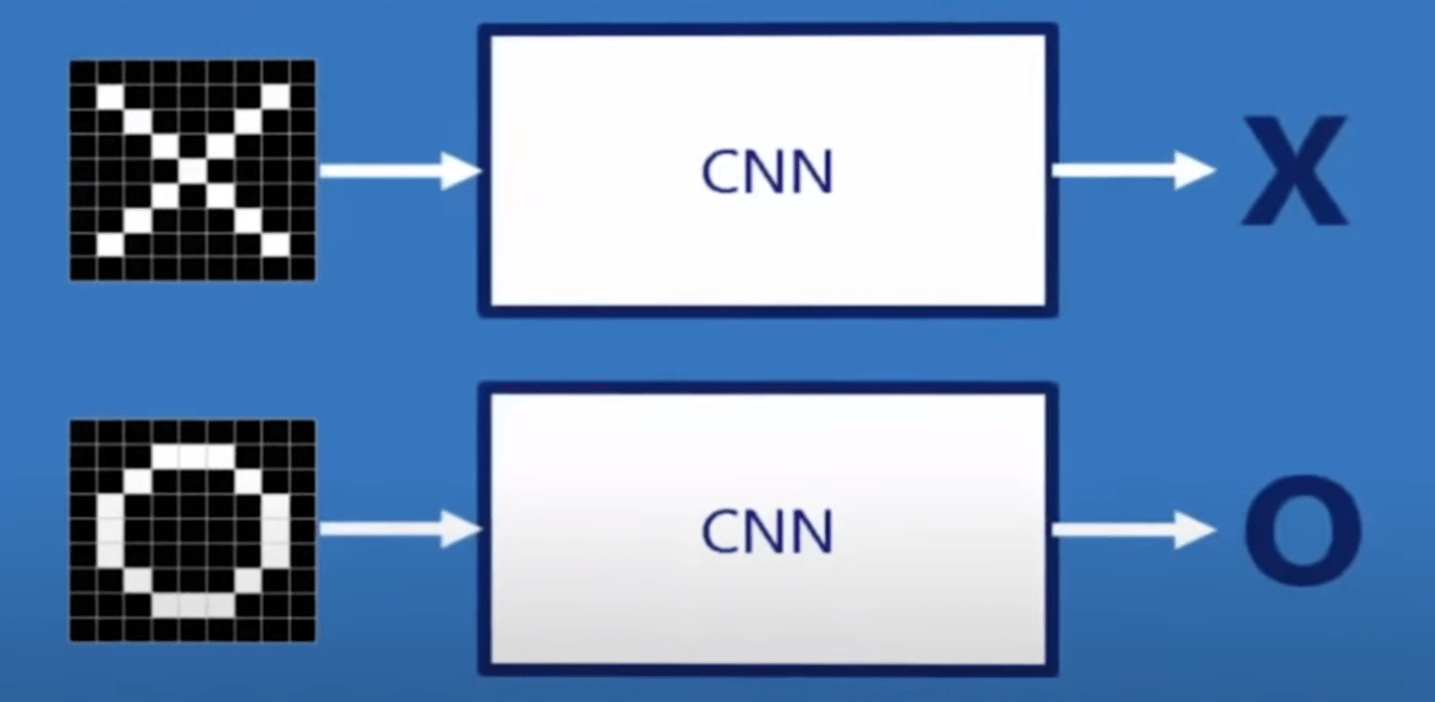
卷积神经网络识别图像的第一步就是把图像的局部特征挑出来（图像进行卷积操作），把局部特征交给神经网络去做判断。

如果挑选的卷积核合适，可以把图像里的某些特征挑出来，其他特征就被过滤掉了。如垂直边界过滤器、水平边界过滤器。

相乘相加是自己对周围像素点的试探，而卷积核则是试探的模板。是对周围像素点的主动试探和选择。

卷积的三层含义

• 一个系统有不稳定输入、稳定输出，就可以通过卷积求系统存量
• 一个卷积核规定周围像素点对当前像素点会产生怎么样的影响
• 一个过滤器的卷积核就是规定一个像素点会如何试探周围的像素点，如何筛选图像特征

感知机

是什么

由罗森布拉特提出。神经网络的基本单元叫感知机。多个输入，一个输出 0、1。是一个分类的工具。

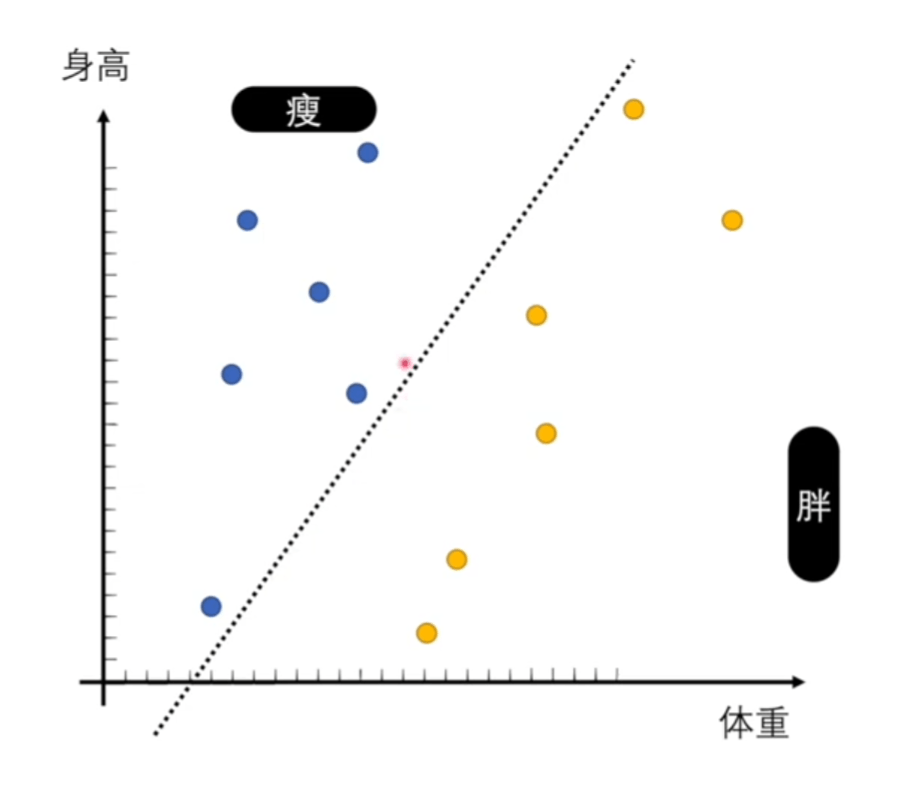
一个感知机至少有两部分，一个分界线，一个数据到底在自己的上面还是下面（二维情况），三维情况就是平面了。只能处理二分问题。

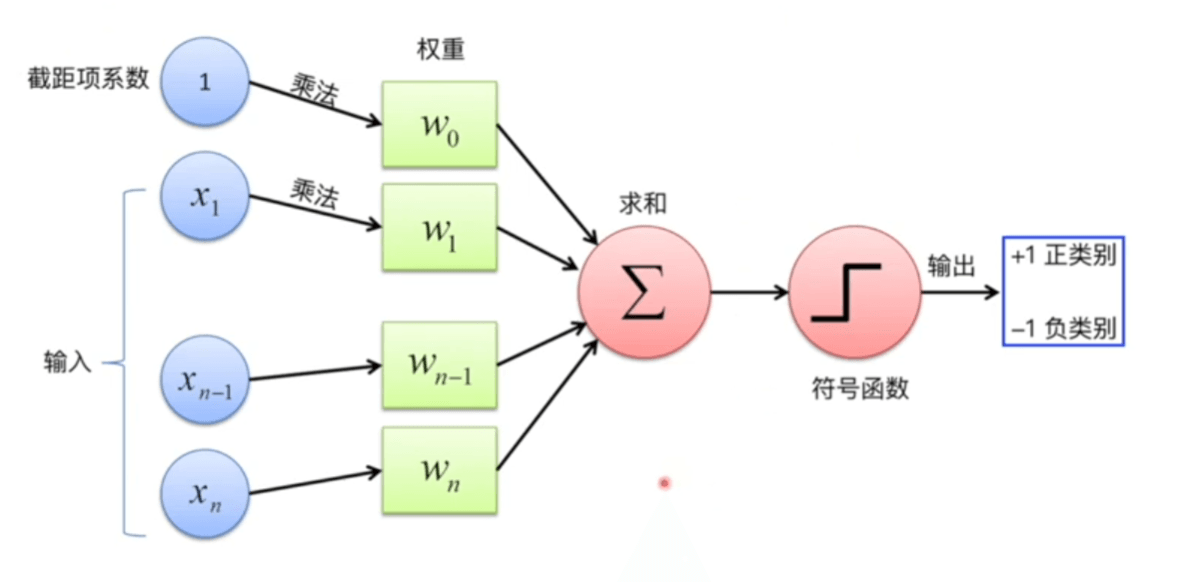
找直接分类的函数的话要去找那个函数能分成几段，分几段呢，每个表达式是什么样子，要不停的去尝试。面对分类问题需要中找到一个统一的模板，所以感知机就是线性二分的模板。体现分而治之的思想。

数学表达式一定有两部分，线性函数、激活函数（判断）。

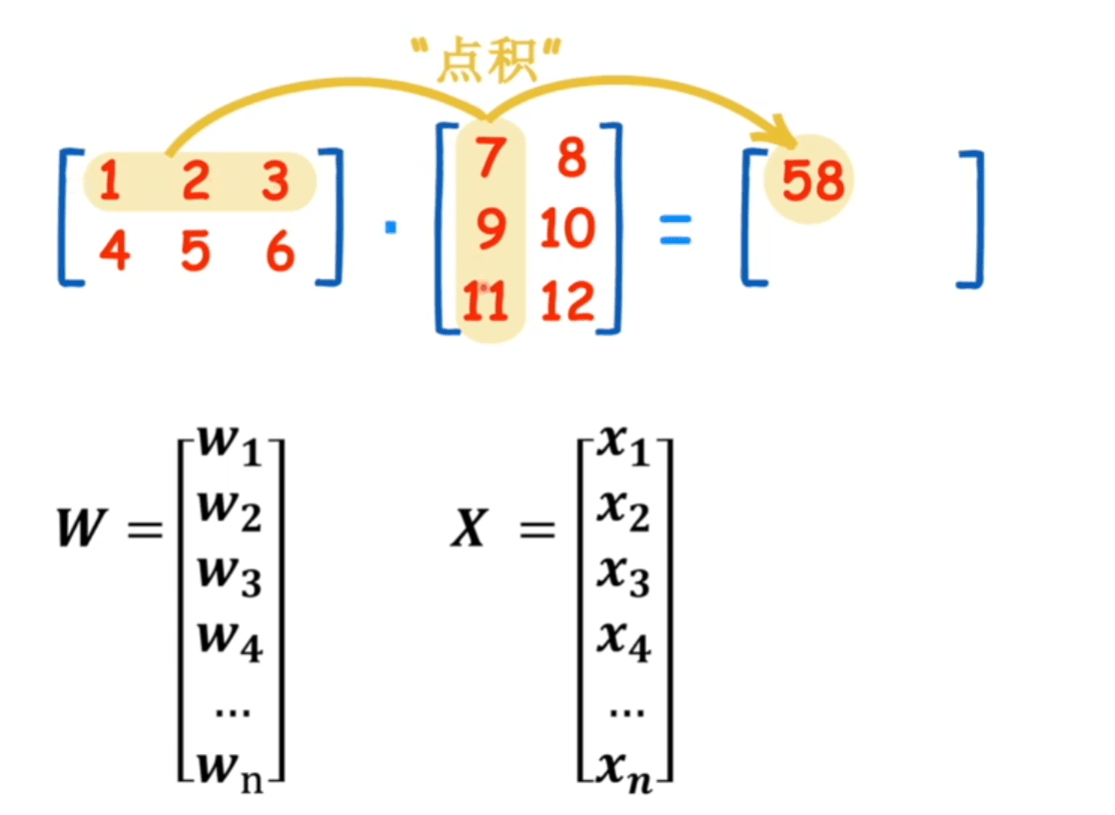
\[t=f\left(\sum_{i=1}^{n} w_{i} x_{i}+b\right)=f\left(\mathbf{w}^{T} \mathbf{x}\right) \]

\[f(n)=\left\{\begin{array}{ll} +1 & \text { if } n \geq 0 \\ -1 & \text { otherwise } \end{array}\right. \]

分界线的具体表示

\[w_{1} \cdot x_{1}+w_{2} \cdot x_{2}+w_{3} \cdot x_{3}+w_{4} \cdot x_{4}+w_{5} \cdot x_{5}+\cdots \cdots+b=0 \]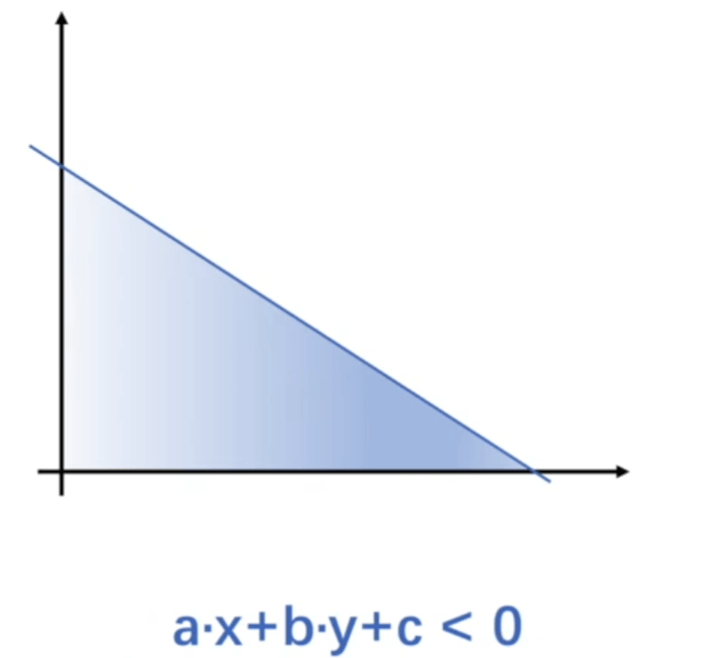

通过判断函数大于0还是小于0就能知道在分界线上面还是下面。

\(w^Tx\) 表达的是两个矩阵的点积关系。\(T\) 符号是矩阵转置。这里只是形式上。\(b\) 也被写到矩阵里了。

感知机的缺陷

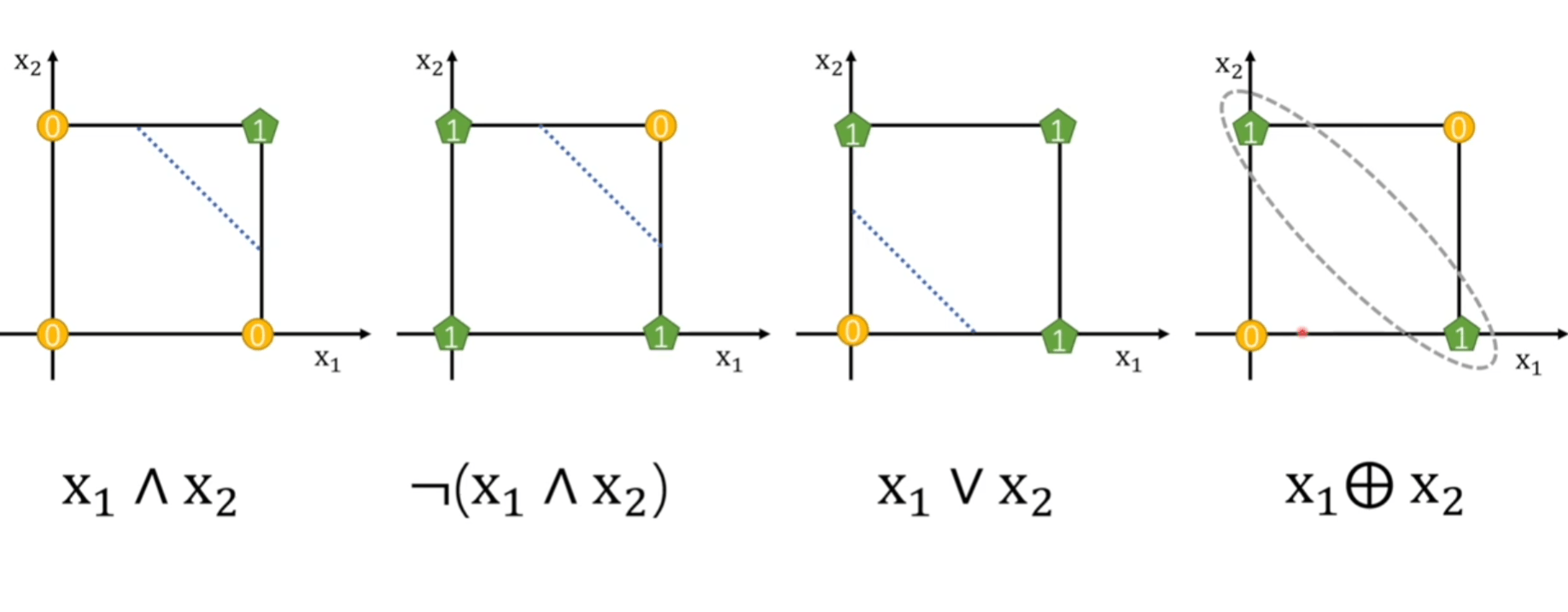
异或没有办法被线性可分。

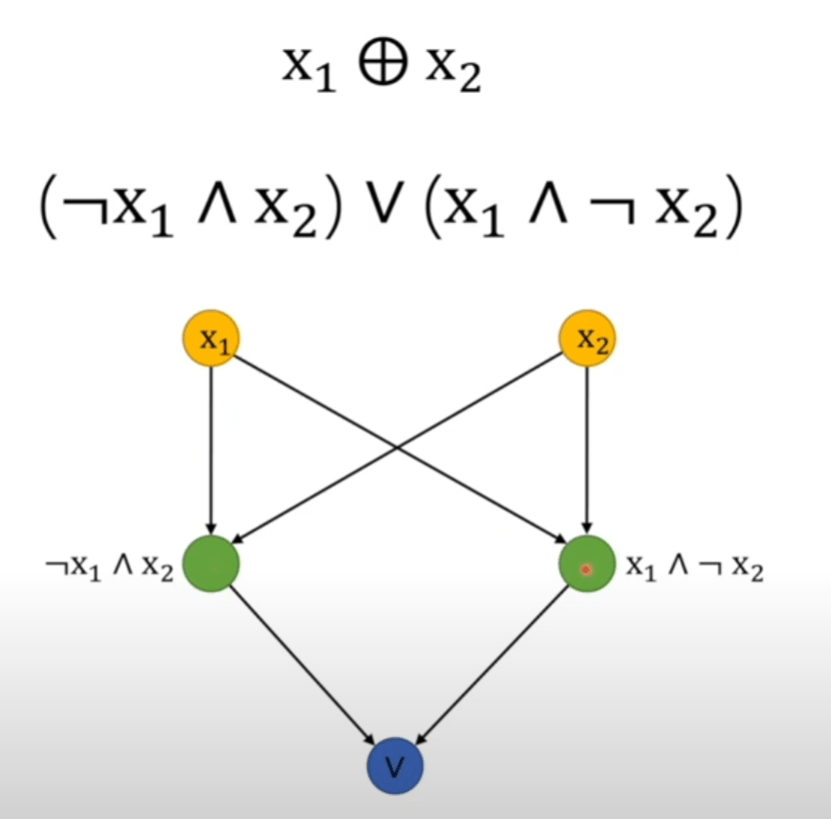
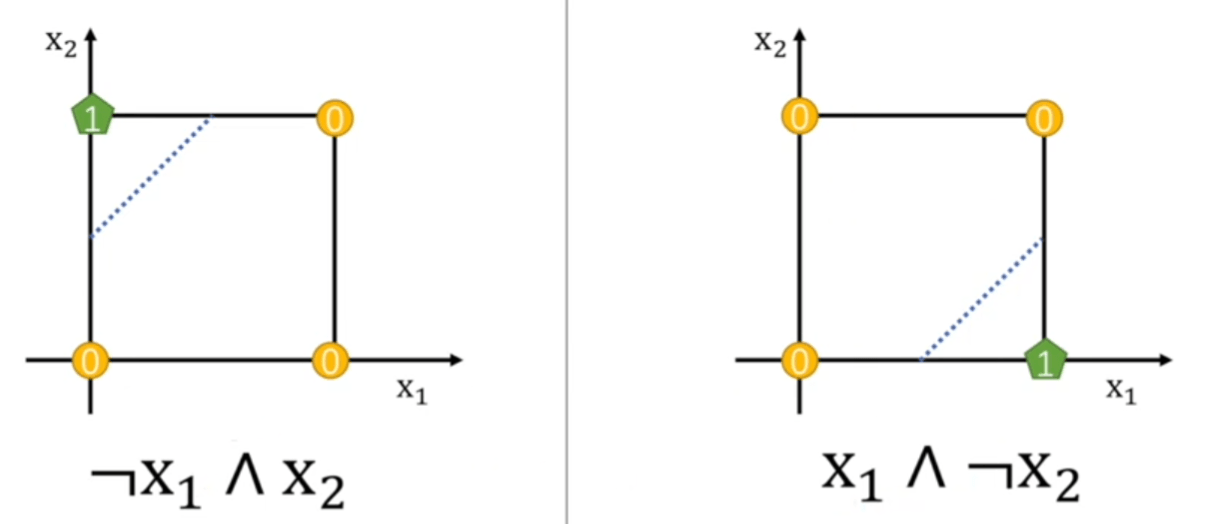
解决方法是输入两个感知机，再把结果给第三个感知机。

通过叠加感知机，实现线性可分。

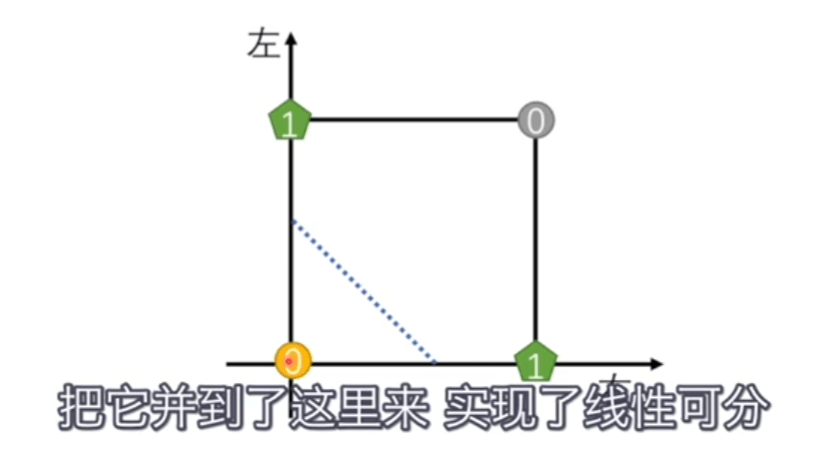
还可以使用升维的方法（盖尔定理），具体升维的方式叫核方法。

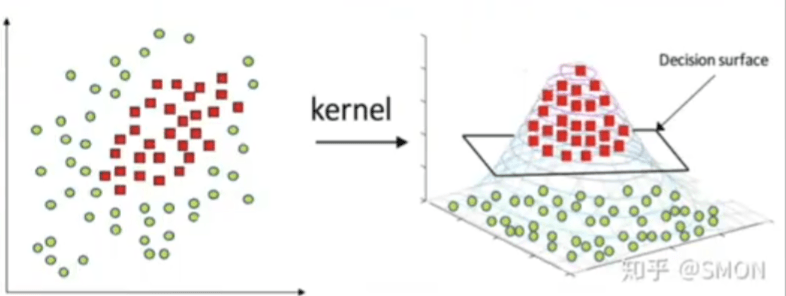
总结

感知机就是分类的模板，一个线性函数加一个激活函数，这个模板能力有限，只能解决线性二分问题，如果是异或非线性问题就有问题，需要用升维或者变形，那么会变成三部分，多一个升维或变形的函数。用多个感知机解决问题会更加简单。

神经网络

是什么

神经网络的基本单元就是感知机。

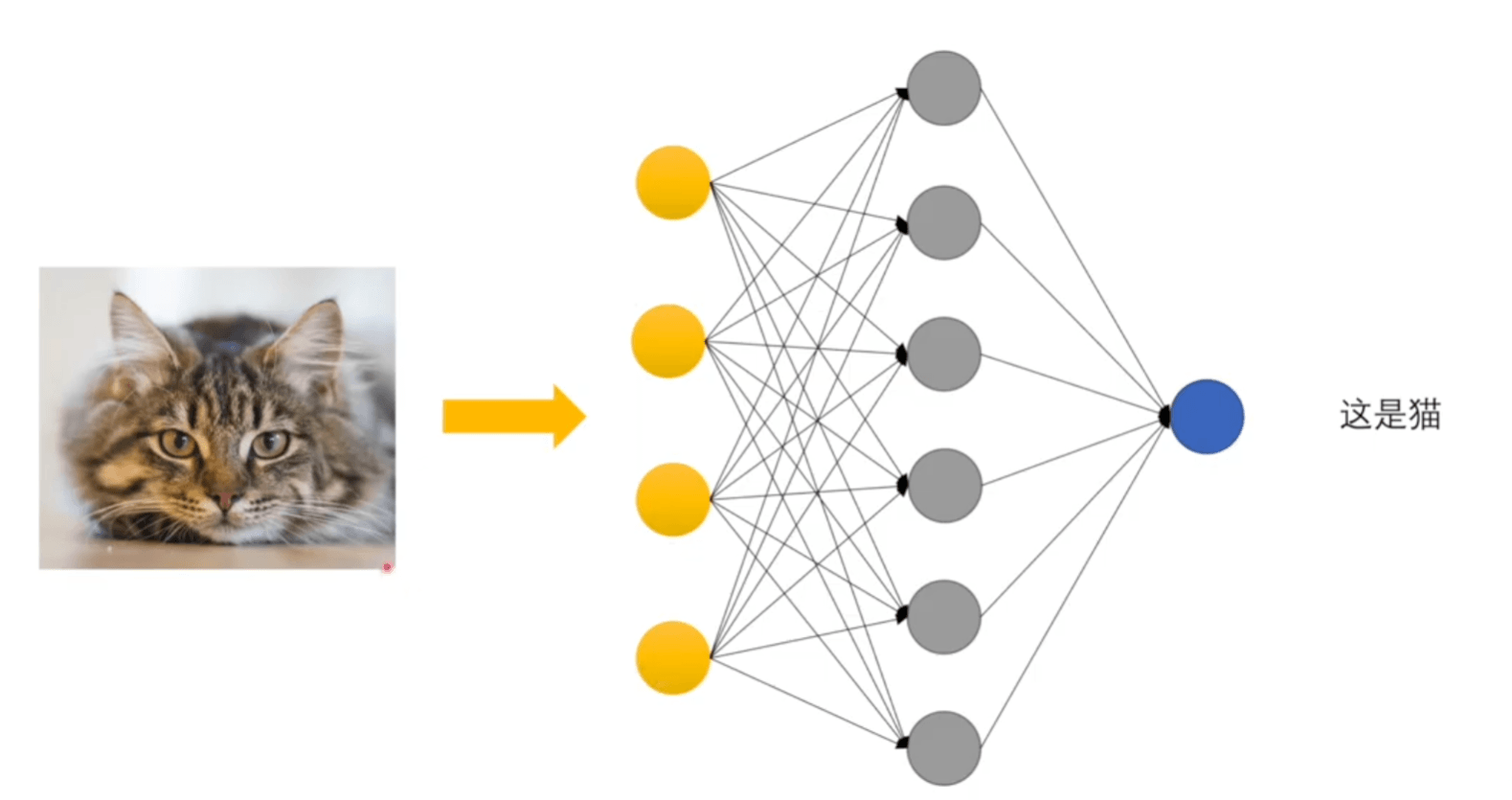
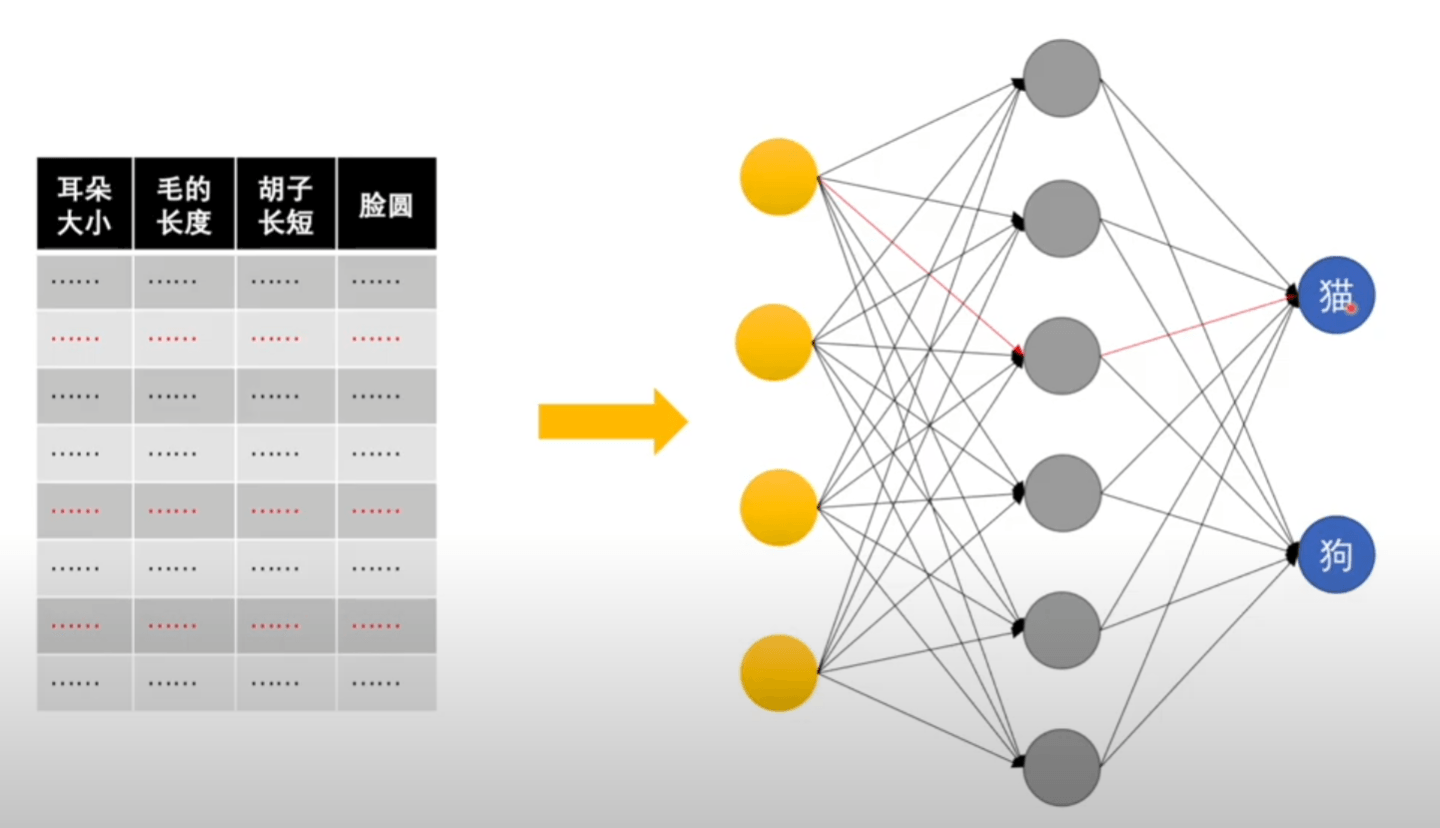
这种可以被称作全神经网络（每个节点都跟下一层节点全部相连）、前馈神经网络（单向）。也有不一样的神经网络。

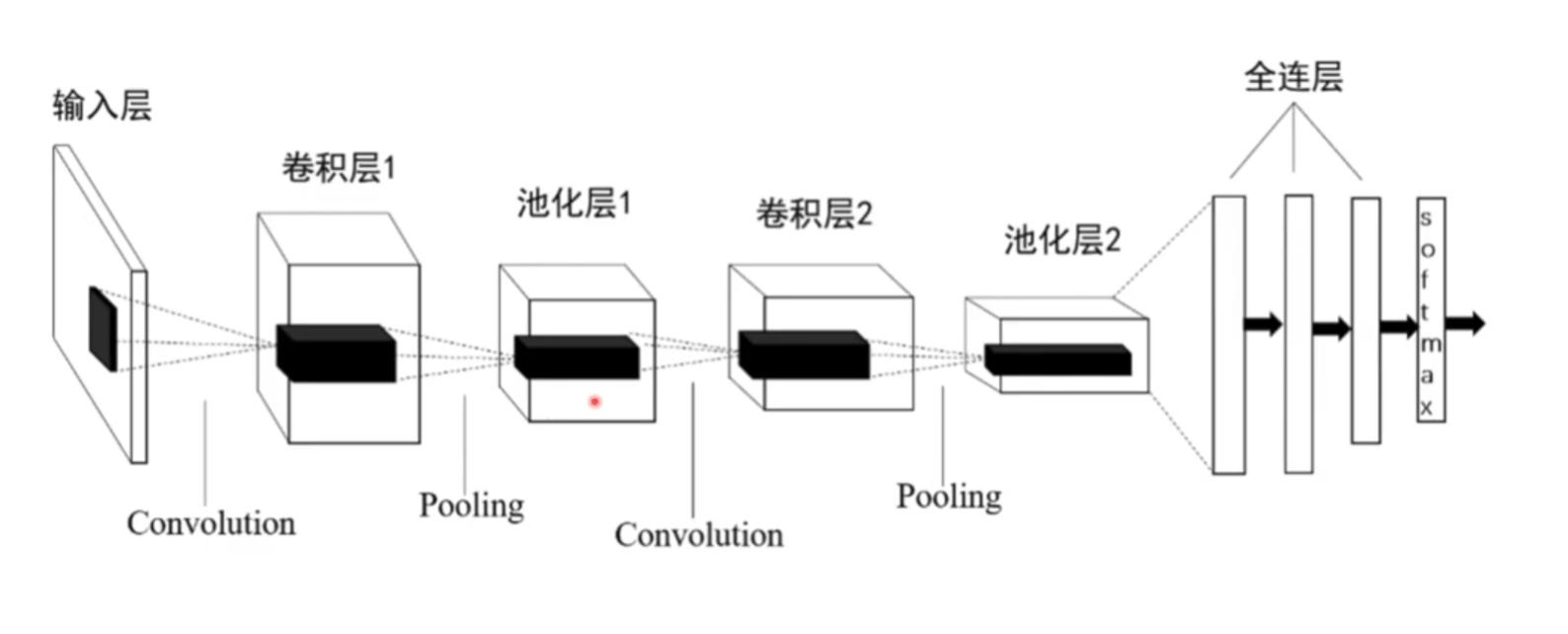
卷积神经网络，不是全连接网络，经过卷积、池化，把数据降维了。

循环神经网络。

缺陷

假如一张图片有200万个像素点，这样输入到神经网络，那么有200万个参数需要被调节。可靠的方法叫梯度下降法，升级成随机梯度下降法，还可以通过卷积、池化降维。

我们给的是肯定的数据，而不是否定的数据，就不能像感知机那样夹逼出分界线。留作之后的问题。

激活函数

激活函数从 0,1 跃迁函数换成了 \(sigmoid\) 函数。感知机的线性函数可以理解成对某个类型里的标准模型的描述，比如对猫的标准模型的描述，激活函数则是判断数据符不符合标准。

我们在真实世界里挑不出一个标准的猫来代替所有的猫，所以我们在理念世界里面抽象创造出一个抽象完美标准的猫神，所有猫是猫神的具象化。训练神经网络本质上就是寻找猫神模型的近似表达。

标签：02,函数,卷积,Machine,感知机,神经网络,图像,像素点
来源： https://www.cnblogs.com/linxiaoxu/p/16101879.html