Dinic Rush
作者:互联网
2022.3.20 模拟赛 T1
之 直角拐弯绳子
因为是私题,所以没有题面。
手玩可得全为偶数的点 能且仅能 为 \(A_0\),全为奇数的点 能且仅能 为 \(A_k\)。
显然是,最小割。如果点 \(P\) 可以通过将数值为偶数的一维 +1 或 -1 变成 \(Q\),那么连边 \(P\to Q\)。
以及生而注定 \(A_0\) 点被源点连,生而注定 \(A_k\) 点把汇点连。
跑最小割即可。
P5934 - [清华集训2012]最小生成树
https://www.luogu.com.cn/problem/P5934
\(u\to v:w\) 存在于最小生成树中,当且仅当连上所有 \(< w\) 的边后,\(u,v\) 不连通。于是最小割即可,最大生成树同理。
如果是要求 \(u\to v:w\) 在所有的最小生成树中,那么将 \(<w\) 改成 \(\le w\)。
P1361 - 小M的作物
https://www.luogu.com.cn/problem/P1361
最大流不行就最小割。
P3980 - [NOI2008] 志愿者招募
https://www.luogu.com.cn/problem/P3980
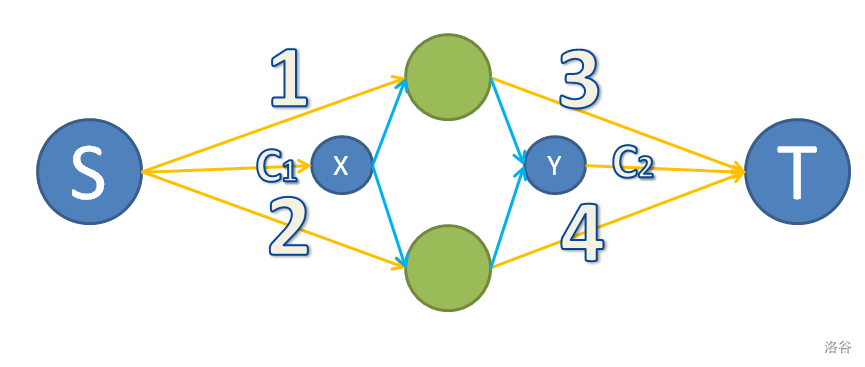
首先看到有两种条件:费用和人数,那么想到费用流
首先建立 \(n\) 个点代表 \(n\) 天,从 S 向 1 连边,\(i\) 和 \(i+1\) 连边,\(n\) 向 T 连边。这些边边权为 \(\inf-a_i\)(S,T的边是 inf),费用是 0.
然后对于一个人,连边 \(s_i\to t_i:[\inf,c_i]\)。流量为 inf,因为有无限个志愿者。
为什么是正确的?考虑如果 \(i\) 号点得到的流量是 inf,那么 \(i+1\) 号点 通过 \(i\to i+1\) 边得到的流量,就是 \(\inf-a_i\),剩下的 \(a_i\) 个流量,就必须要通过「人」边来传递了!
P7425 - [THUPC2017] 机场
https://www.luogu.com.cn/problem/P7425
与上题原理相同。然而我懒得看题面
FROM https://www.luogu.com.cn/training/1230#problems
CF311E - Biologist
https://www.luogu.com.cn/problem/CF311E
最大权闭合子图问题。(此问题的模板https://blog.csdn.net/can919/article/details/77603353)
先把原串全变成 1,然后计算此时的答案,ans0 =【所有变 1 要求的奖励之和】-【 0 变成 1 的所有 \(v_i\) 】-【非法的要求的赔偿之和】。
如果想满足一个要求,就要满足所有的 0,1 都匹配,于是想到最大权闭合子图。
我们给原串的 \(n\) 个位置,建立相应的 \(n\) 个点。对于 \(m\) 个要求,也建立相应的 \(m\) 个点。
对于一个变 0 要求,连边它到所有所需位置的原串点,权值为 inf。然后源点给他连上边权为 \(w+g\) 的边(相当于反悔)。
对于一个变 1 要求,连边所有位置到它所需位置的原串点,权值为 inf。然后他给汇点连上 \(-w-g\) 的边。
答案就是 所有正权边 减去 最小割(注意:事实上跑最小割时,边权都是绝对值)再加上原来的 ans0。
注:事实上发现答案加上 ans0,刚好就是 \(\sum w\) 减去 最小割。
P6054 - [RC-02] 开门大吉
https://www.luogu.com.cn/problem/P6054
算出 \(i\) 人答 \(j\) 题的期望得分 \(v(i,j)\)。
这种分配的问题,考虑最小割。
那么考虑给每个人弄一个“答题链”,也就是 \(dot(i,j),j\in [1,m]\),然后相邻的点连边 \(v(i,j)\)。如此做出,则【刚好答一套题】就是【割掉一条边】。
对于限制:第 \(i\) 个人比第 \(j\) 个人大 \(k\),连边 \(dot(j,x),dot(i,\ \min(m,x+k)\ )\),容量为 inf,代表如果 \(i,j\) 相差小于 \(k\) 那么 就会导致流 inf 边流过。
P2053 - [SCOI2007]修车
https://www.luogu.com.cn/problem/P2053
对于每个人的等待时间不好考虑,转而考虑每辆车会对答案产生多少贡献。
不难看出,如果第 \(i\) 辆车是第 \(j\) 位技术人员倒数第 \(k\) 个修的,那么就会产生 \(k*cost_{i,j}\) 的代价。
那么我们把每个技术人员拆成 \(k\) 个点,每个点表示倒数第 \(k\) 个进行的工作,每个结点连的边的费用也就乘以对应的 \(k\) 倍。
由于费用流的最优性,这些点一定是顺次选取的。
P4043 - [AHOI2014/JSOI2014]支线剧情
https://www.luogu.com.cn/problem/P4043 之 galgame 玩家
首先保证每个点至少流量为 1.然后还要求费用最小。
这把 【费用 + 可行流】写在脸上了。不愧是 2014 的题目。
标签:www,cn,luogu,Rush,https,Dinic,inf,com 来源: https://www.cnblogs.com/BlankAo/p/16084016.html