多层语法糖,有参函数,递归函数,二分法等
作者:互联网
语法糖
语法糖(Syntactic sugar):
计算机语言中特殊的某种语法
这种语法对语言的功能并没有影响
对于程序员有更好的易用性
能够增加程序的可读性
'''
简而言之,语法糖就是程序语言中提供的一种手段和方式而已。 通过这类方式编写出来的代码,即好
看又好用,好似糖一般的语法。美其名曰:语法糖。
'''
装饰器--多层语法糖
Python 的装饰器能够在不破坏函数原本结构的基础上,对函数的功能进行补充。当我们需要对一个函数补
充不同的功能,可能需要用到多层的装饰器。
def deco1(func):
print(1)
def wrapper1():
print(2)
func()
print(3)
print(4)
return wrapper1
def deco2(func):
print(5)
def wrapper2():
print(6)
func()
print(7)
print(8)
return wrapper2
@deco1
@deco2
def foo():
print('foo')
foo()
执行结果:
5
8
1
4
2
6
foo
7
3
1.修饰器本质上就是一个函数,只不过它的传入参数同样是一个函数。因此,依次加了deco1和deco2两个装饰器的原函数foo实际上相当于deco1(deco2(foo))。
2.明白了第1步后,下面进入这个复合函数。首先执行的是内层函数deco2(foo)。因此第一个打印值是5。接下来要注意,在deco2这个函数内定义了一个wrapper2函数,但是并没有类似于wrapper2()的语句,因此该函数内的语句并没有立即执行,而是作为了返
回值。因此wrapper2内的3条语句作为输入参数传递到了deco1内。wrapper2函数内还有一行print(8),因此第二个打印值为8。
3.下一步是执行deco1()函数内容。与2类似,先打印出1和4,返回值为wrapper1。由于更外层没有装饰器,因此接下来就将执行wrapper1内的内容。第五个打印值为2。接着执行func()函数,注意此处func()表示的是wrapper2中的内容,因此跳到wrapper2中
执行。第六个打印值为6。类似的,wrapper2中的func()为foo(),因此接着会输出foo。最后,回到wrapper2和wrapper1的最后一行,依次输出7和3。到这里,整个装饰器的运行过程结束。
有参装饰器
实际是对原有装饰器的一个函数的封装,并返回一个装饰器(一个含有参数的闭包函数)
当使用@f4(0)调用的时候,Python能发现这一层封装,并将参数传递到装饰器的环境去
import time
def f4(flag = 0):
def f1(func):
def f2(*args,**kwargs):
t1 = time.time()
func(*args,**kwargs)
t2 = time.time()
print(t2 - t1)
print(flag)
return f2
return f1
@f4(0)
def f3(*args,**kwargs):
print('春游去动物园')
time.sleep(1)
f3(1,2,3)
'''
有参装饰器目的仅仅是给装饰器传递额外的参数
装饰器最多就三层嵌套
并且三层嵌套的结构使用频率不高(最多是使用别人写好的有参装饰器)
'''
递归函数
在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数。
递归函数特性:
1.必须有一个明确的结束条件;
2.每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3.相邻两次重复之间有紧密的联系,前一次要为后一次做准备(通常前一次的输出就作为后一次的输入)。
4.递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
例一:
先举个简单的例子:计算1到100之间相加之和;通过循环和递归两种方式实现
# 循环方式
def sum_cycle(n):
sum = 0
for i in range(1,n+1) :
sum += i print(sum)
# 递归方式
def sum_recu(n):
if n>0:
return n +sum_recu(n-1)
else:
return 0
sum_cycle(100)
sum = sum_recu(100)
print(sum)
例二:
使用递归函数实现数学中的阶乘6!(1*2*3*4*5*6)
def f1(n):
if n < 1:
return 1
else:
return n*f1(n-1)
a = f1(6)
print(a) # 720
最大递归限制(深度):官网给出的是1000
import sys
print(sys.getrecursionlimit()) # 获取默认的最大递归深度1000
sys.setrecursionlimit(2000) # 还可以修改最大递归深度
算法----二分法
最早接触二分法是在高中的时候,那个时候我们是叫它对分查找,但是逻辑是一样的。
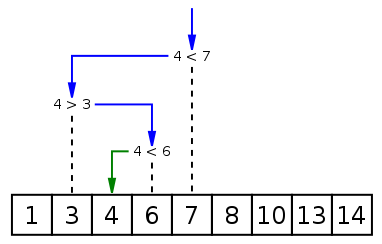
二分搜索是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从
中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半
arr = [2, 3, 4, 10, 40]
max = len(arr)
def select_num(arr_list, r, max, min=0):
if max >= min:
# 获取中间元素的索引值
mid = (max + min) // 2
if arr_list[mid] == r:
print('找到了')
return
if r < arr[mid]: # 元素小于中间位置的元素,只需要再比较左边的元素
return select_num(arr_list, r, mid - 1, min)
else: # 元素大于中间位置的元素,只需要再比较右边的元素
return select_num(arr_list, r, max, mid + 1)
else:
# 不存在
print('找不到')
return
select_num(arr, 4, max) # 找到了
select_num(arr, 1, max) # 找不到
"""
二分法的缺陷
1.如果要找的元素就在数据集的开头 二分更加复杂
2.数据集必须有顺序
目前没有最完美的算法 都有相应的限制条件
"""
标签:wrapper2,return,函数,递归函数,sum,多层,二分法,print,def 来源: https://www.cnblogs.com/chunyouqudongwuyuan/p/16035090.html