AtCoder Grand Contest 013&014

013D Piling Up

题目描述

点此看题

解法

还是把一开始的球确定了好 \(dp\)，否则写出来的 \(dp\) 奇奇怪怪还不好优化。

枚举初始时有 \(x\) 个白球 \(n-x\) 个黑球，注意每一轮之后球数都是 \(n\)，可以设 \(dp[i][j]\) 表示前 \(i\) 轮过后有 \(j\) 个白球对应序列方案数，我们考虑这一轮放置的方法可以得到这样的转移：

• 若 \(j\geq1\)，先放置白球：\(dp[i][j-1]\leftarrow dp[i-1][j]\)，\(dp[i][j]\leftarrow dp[i-1][j]\)
• 若 \(j\leq n\)，先放置黑球：\(dp[i][j+1]\leftarrow dp[i-1][j]\)，\(dp[i][j]\leftarrow dp[i-1][j]\)

其实我们不需要枚举，由于转移方式都是相同的，我们做整体 \(dp\) 就行了（本题体现为多点初始化）

但是这样会算重，考虑两种不同的初始状态可能对应着相同的序列，但是放在坐标上是同构的：

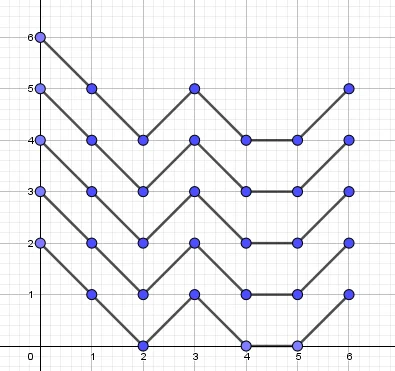
所以我们强制路径碰到 \(j=0\) 就可以不算重了，这只需要在状态中增加一维。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std; 
const int M = 3005;
const int MOD = 1e9+7;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,w,ans,f[2][M][2];
void add(int &x,int y) {x=(x+y)%MOD;}
void work()
{
	w^=1;memset(f[w],0,sizeof f[w]);
	for(int j=0;j<=n;j++)
	{
		int a=f[w^1][j][0],b=f[w^1][j][1];
		if(j>=1)
		{
			//bb
			if(j==1) add(f[w][j-1][1],a);
			else add(f[w][j-1][0],a);
			add(f[w][j-1][1],b);
			//bw
			if(j==1) add(f[w][j][1],a);
			else add(f[w][j][0],a);
			add(f[w][j][1],b);
		}
		if(j<n)
		{
			//ww
			add(f[w][j+1][0],a);
			add(f[w][j+1][1],b);
			//wb
			add(f[w][j][0],a);
			add(f[w][j][1],b);
		}
	}
}
signed main()
{
	n=read();m=read();
	f[0][0][1]=1;
	for(int i=1;i<=n;i++) f[0][i][0]=1;
	for(int i=1;i<=m;i++) work();
	for(int i=0;i<=n;i++) add(ans,f[w][i][1]);
	printf("%d\n",ans);
}

标签：AtCoder,Contest,int,leftarrow,add,013,白球,include,dp
来源： https://www.cnblogs.com/C202044zxy/p/15957474.html