[ICLR 2021] Revisiting Dynamic Convolution via Matrix Decomposition 学习笔记
作者:互联网
[ICLR 2021] Revisiting Dynamic Convolution via Matrix Decomposition
摘要
该文章表明,K个静态卷积核的自适应聚合所得到的动态卷积效果较好,但其存在两个主要的问题:
-
卷积权重数量增加了K倍。
-
动态注意力和静态卷积核的联合优化具有挑战性。
文章从矩阵分解的角度揭示了动态卷积的本质,即动态卷积是在投影到高维隐空间后对通道组应用动态关注。因此,本文提出动态通道融合来取代对通道组的动态关注。这样有两个好处:降低隐空间的维度以及减轻联合优化的难度,使得网络更容易训练,且相比于传统的动态卷积而言参数量大幅度降低。
Dynamic Convolution Decomposition
文章首先介绍了动态卷积的发展历程,对于2019年提出的CondConv其基本思想是利用注意力机制将多个动态卷积核动态聚集到一个卷积核之中。有公式:
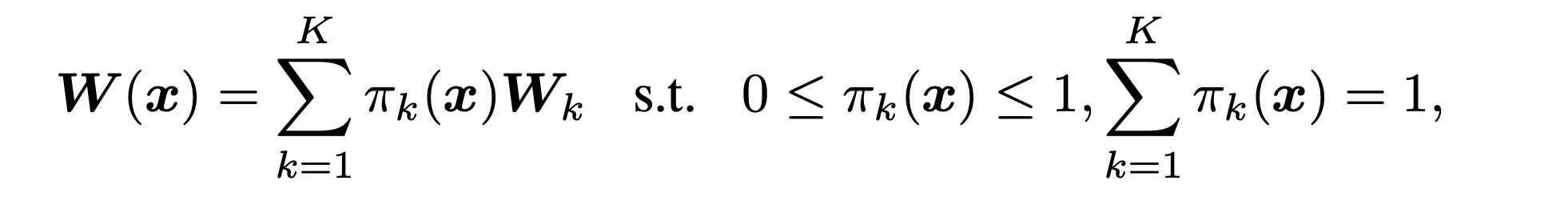
表示k个卷积核通过作用于其的注意力分数聚集在一起,其中注意力分数之和为1。但是这样的动态卷积有两个主要的限制:使用K个卷积核缺乏紧致性,以及注意力分数和静态核的联合优化具有挑战性。
在本篇文章的工作中,作者通过矩阵分解的角度重新审视这两个问题。首先作者用残差重新表述动态卷积:
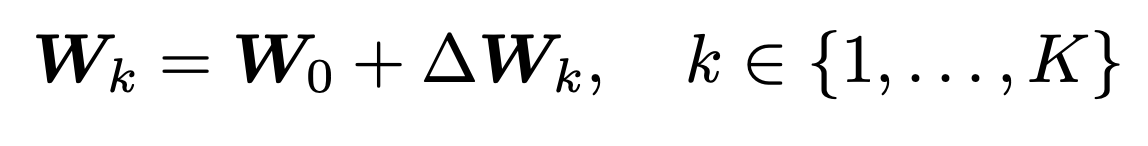
其中\(W_0=\frac{1}{K}\Sigma_{k=1}^KW_k\)为均值核,\(\Delta W_k=W_k-W_{0}\)为残差权重矩阵。对于这个残差矩阵可以进一步进行SVD分解:\(\Delta W_k=W_k-W_{0}=U_kS_kV_k^T\),得到最终的变换形式:
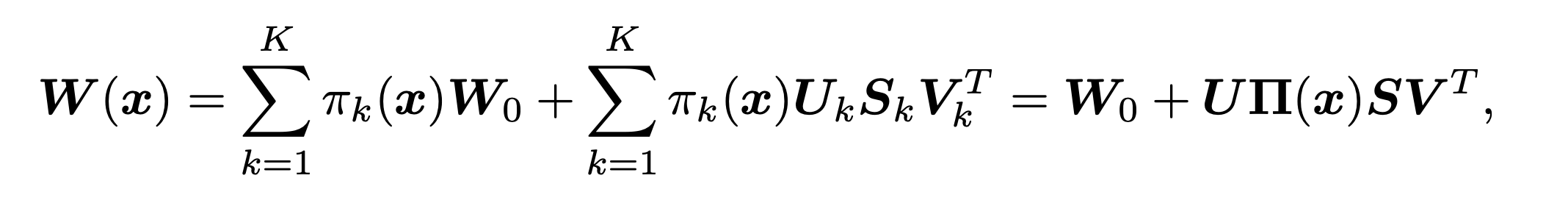
这里简单介绍一下SVD分解。SVD分解即奇异值分解,其在机器学习领域被广泛应用。他不仅可以用于降维算法中的特征分解,还可以用于推荐系统等领域。
提到奇异值分解,必须要先说一下特征值分解:将矩阵A分解为\(A=Q\Sigma Q^{-1}\),其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么。但其最主要的局限是进行变换的矩阵必须为方阵。而奇异值分解可以作用于任意矩阵。
具体来说,一个矩阵进行SVD分解后会得到三个矩阵相乘的形式:\(A=U\Sigma V^T\),U为n阶酉矩阵(左奇异向量矩阵),\(\Sigma\)为非负实数对角矩阵,\(V^T\)是V的共轭转置,也叫右奇异矩阵。\(\Sigma\)对角线的元素即为A的奇异值。奇异值与特征值的关系可以参考知乎的这个回答:https://www.zhihu.com/question/19666954
同时在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,可以用前r大的奇异值来近似描述矩阵,定义部分奇异值分解:
因此可以用近似奇异值分解的方式压缩表示原矩阵。
上图可以看到K个核对应的注意力分数作用于对角矩阵\(S_i\),即实际上是对特征向量的重要性施加注意力。
这里有一个问题,一般来说卷积核矩阵都是方阵,为什么这里采用SVD分解而非特征分解呢?个人猜想可能的原因:SVD分解更能表示内在的本质;SVD分解可以实现原矩阵的压缩表示。
公式表明,W(x)的动态行为是由动态残差\(UΠ(x)SV^T\)实现的,它将输入x投射到一个更高维的空间\(SV^Tx\)(从C到KC通道),在通道组上应用动态注意力\(Π(x)\),并通过与U相乘,将维度还原到C通道。这里的更高维空间个人理解就是通过K个卷积核张成的,因为论文中提到了\(S=diag(S_1,...,S_K),V =[V_1,...,V_K]\)。也可以看上面的图来理解。
原文说,这表明普通的动态卷积的局限性是由于在通道组上使用注意力,这诱发了一个高维的隐空间,导致小的注意力值可能抑制相应通道的学习。因为基于下式:
较小的注意力分数可能会抑制ui, vi这些相应列的学习。
因此,为了解决这个问题,作者提出了动态卷积分解(dynamic convolution decomposition,DCD),以动态通道融合的方式取代了对于通道组的动态关注。DCD主要是基于一个全动态矩阵Φ(x),其中每一个元素 φi,j (x) 都是输入x的一个函数。动态矩阵分解以下图方式进行:
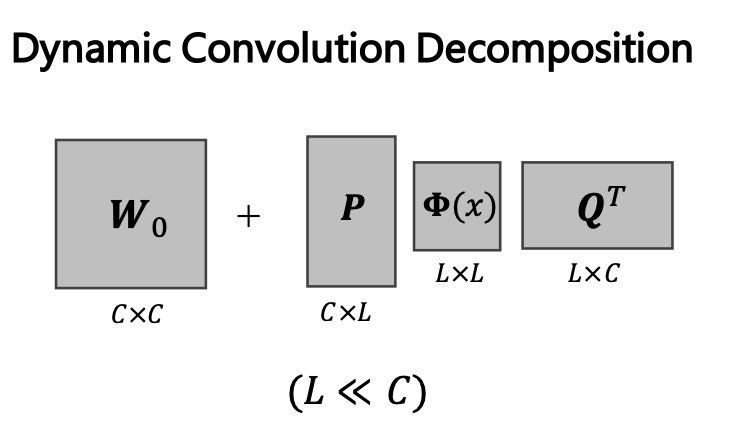
其中P和Q是两个动态矩阵,Q进行降维,将输入压缩到低维隐空间,φ(x)对这个空间的通道进行动态融合,最终靠P将通道数量扩展到输出空间。因此,P、Q的参数量得以明显减少。同时这也解决了之前提到的联合优化困难的问题:因为P , Q的每一列都与Φ(x)的多个动态系数相关,因此,几个小的动态系数不足以抑制静态矩阵P , Q的学习。
论文先假设W具有相同数量的输入和输出通道(Cin = Cout = C),并忽略了偏置项,重点讨论1×1卷积,并在后面推广到k×k的情形。
动态通道融合的表达式如下:
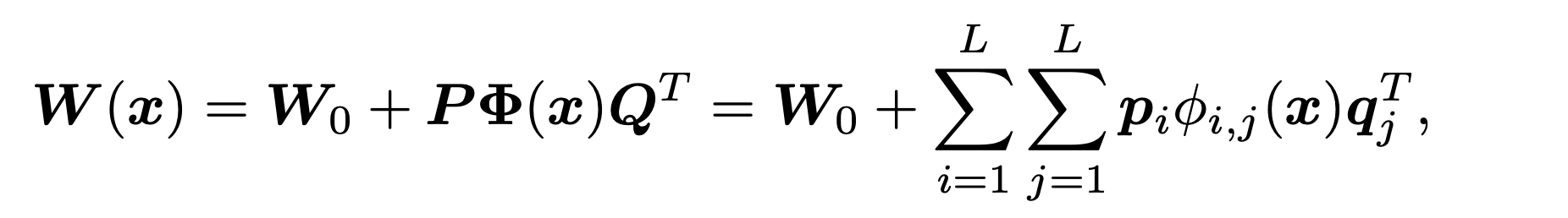
这里的L是人为限制的,L代表隐空间的维度,需要满足\(L^2<C\)。原文取\(L=\lfloor \frac{C}{2^{\lfloor log_2 \sqrt{c} \rfloor}}\rfloor\)
由于这样的设计,使得参数量大大减少,从而得到一个更为紧致的模型。总结如下:IDCD uses an unshared dynamic channel fusion mechanism to aggregate shared static basis vectors in a low dimensional latent space.
接下来原文对静态核\(W_0\)进行了讨论。对注意力分数和为1这个限制进行松弛后,得到更一般的表述:
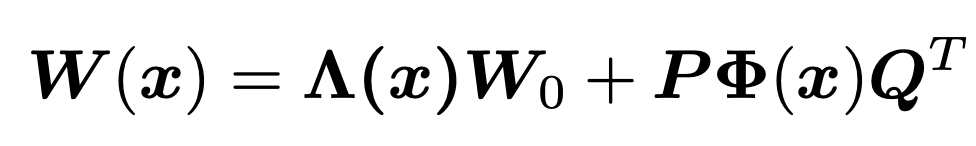
其中Λ(x)为C阶对角方阵,表明其在静态核上施加了通道级的注意力。文章提及了其与SE的不同:首先Λ(x)与卷积并行共享输入,它可以被认为是一个动态卷积核\(y = (Λ(x)W_0)x\)或一个应用于卷积\(y = Λ(x)(W_0x)\)输出特征图的输入依赖性注意力机制,因此计算复杂度为\(min(O(C^2), O(HWC))\);而SE以卷积的输出作为输入,计算复杂度为\(O(HWC)\)。
(这里不是特别理解\(min(O(C^2), O(HWC))\)这个复杂度是怎么算出来的==
接下来作者提到了动态卷积层的实现,主要看如下两张图:
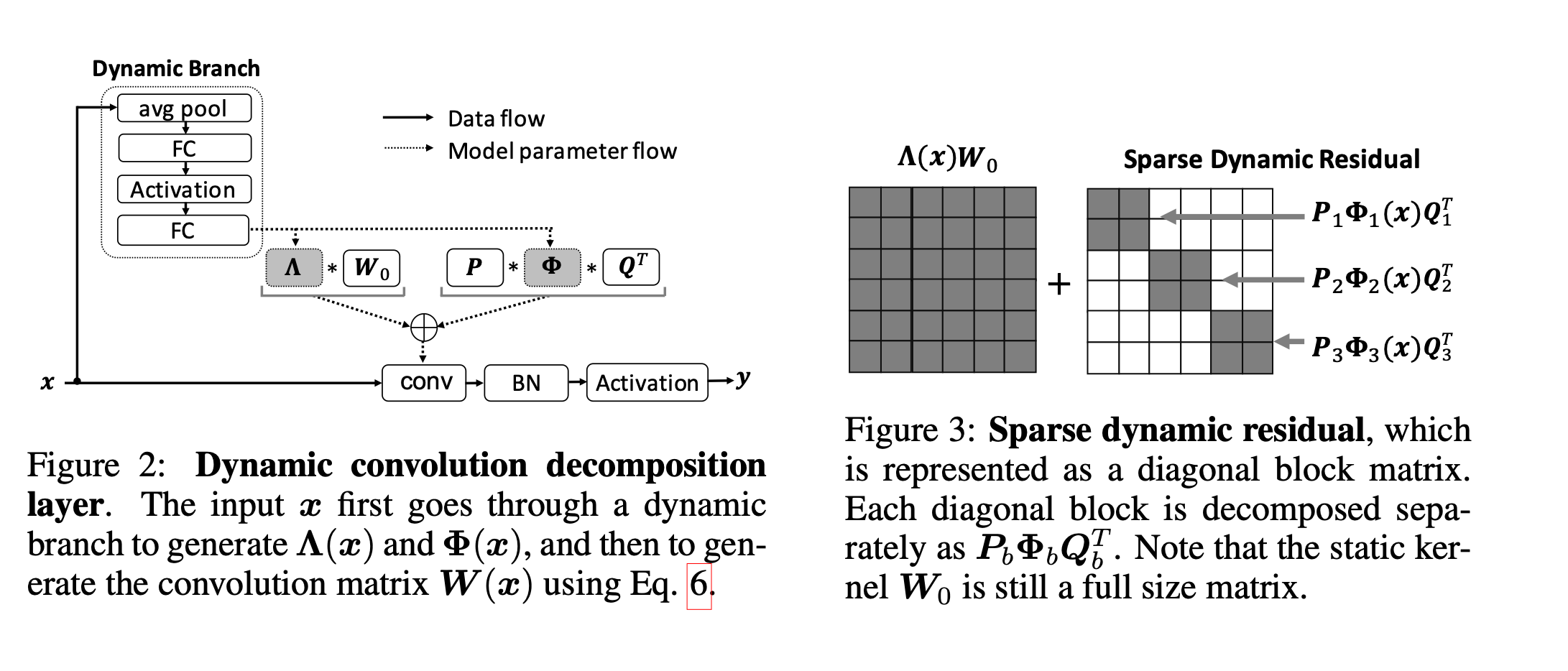
整体结构和CondConv类似,动态分支先对输入x做一个平均池化,然后是两个全连接层中间夹一个激活层,第一个全连接层通过r减少通道的数量,第二个全连接层扩展为\(C+L^2\)的输出(\(C\ for\ Λ\ and\ L^2\ for\ Φ\))。这一部分文章主要聚焦参数的复杂度:静态卷积为\(C^2\),动态卷积为\(KC^2\),DCD所需为\(C^2+2CL+(2C+L^2)\frac{C}{r}\),且由之前的限制\(L^2<C\),当选择r = 16时总参数量为\(1\frac{3}{16}C^2\),远小于常规动态卷积的参数量。
之后文章以三种方式进行扩展:稀疏动态残差、\(k\times k\)深度卷积以及\(k\times k\)卷积。
稀疏动态残差
动态残差\(PΦ(x)Q^T\)可以被进一步表示为块对角矩阵的形式:\(P_bΦ_b(x)Q^T_b ,b ∈ {1,...,B}\)。
注意此时静态核\(W_0\)仍然是全矩阵,仅有动态残差部分是稀疏的,如下图:
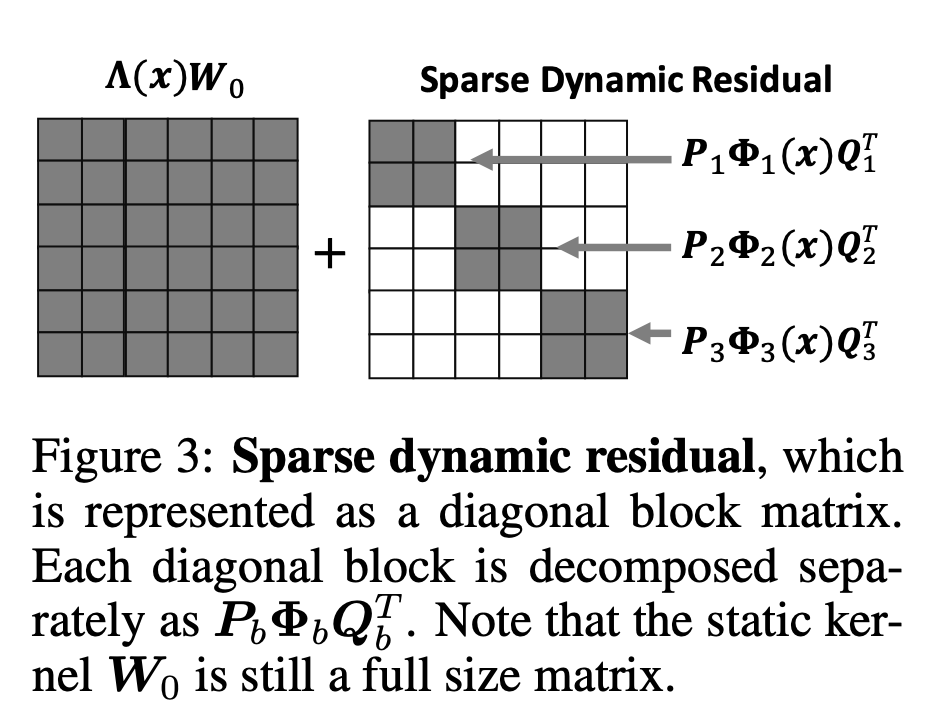
别的博客对这篇论文的解读说上图是B=1的特殊情况,个人感觉是笔误,因为上图的B按照论文的意思明显为3。
文章表明B=8的时候性能下降最小,但仍优于静态核的性能。
DCD OF k × k 深度卷积
k × k 深度卷积构造得到了\(C\times k^2\)的矩阵。DCD可以通过将之前公式中的矩阵Q(压缩通道的数量)替换为矩阵R(压缩核元素的数量):\(W(x)=Λ(x)W_0 +PΦ(x)R^T,\)
其中\(W(x)\)和\(W_0\)都是\(C\times k^2\)矩阵,\(Λ(x)\)为\(C\times C\)的对角阵(实现了通道级注意力),\(R\)是\(k^2\times L_k\)的矩阵(将核元素的数量从\(k^2\)缩减为\(L_k\)),\(Φ(x)\)是\(L_k\times L_k\)矩阵(对\(L_k\)个隐核元素进行动态融合),\(P\)是\(C\times L_k\)的矩阵。\(L_k\)的缺省值取\(\lfloor k^2/2\rfloor\)。由于深度卷积是通道可分离的,Φ(x)不融合通道,而是融合Lk个隐核元素。
DCD OF k × 卷积
对于通道和内核元素的联合融合:一个\(k×k\)卷积核形成一个\(C×C×k^2\)张量。因此DCD可以按照如下公式进行扩展:\(W(x)=W_0 ×_2 Λ(x)+Φ(x)×_1Q×_2 P ×_3 R\)
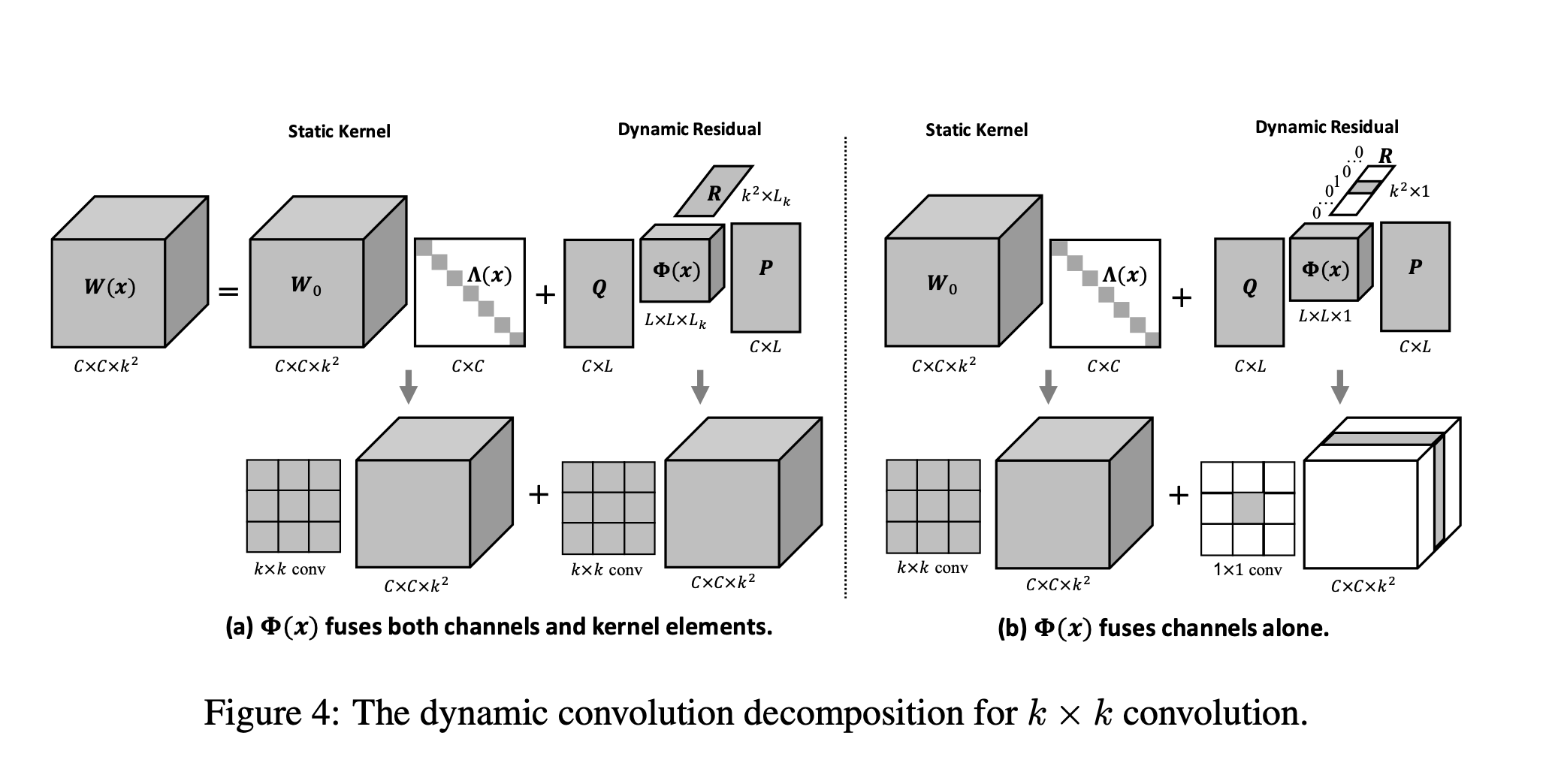
同时对于单纯的通道融合,作者提到\(Φ(x)×_1 Q\)比\(Φ(x)×_3 R\)更重要。如果将\(L_k\)降低到1,同时对\(L\)进行提升,此时R被简化为一个独热向量。上图(b)中动态残差仅有一个非零片,相当于\(1\times 1\)卷积。因此,k×k卷积的DCD本质上是将1×1的动态残差加入到静态的k×k的静态核中。
实验
作者在ImageNet数据集上进行了一系列的实验。选择的baseline为MobileNetV2以及ResNet18。
首先作者对比了不同的DCD的模型,结果如下:
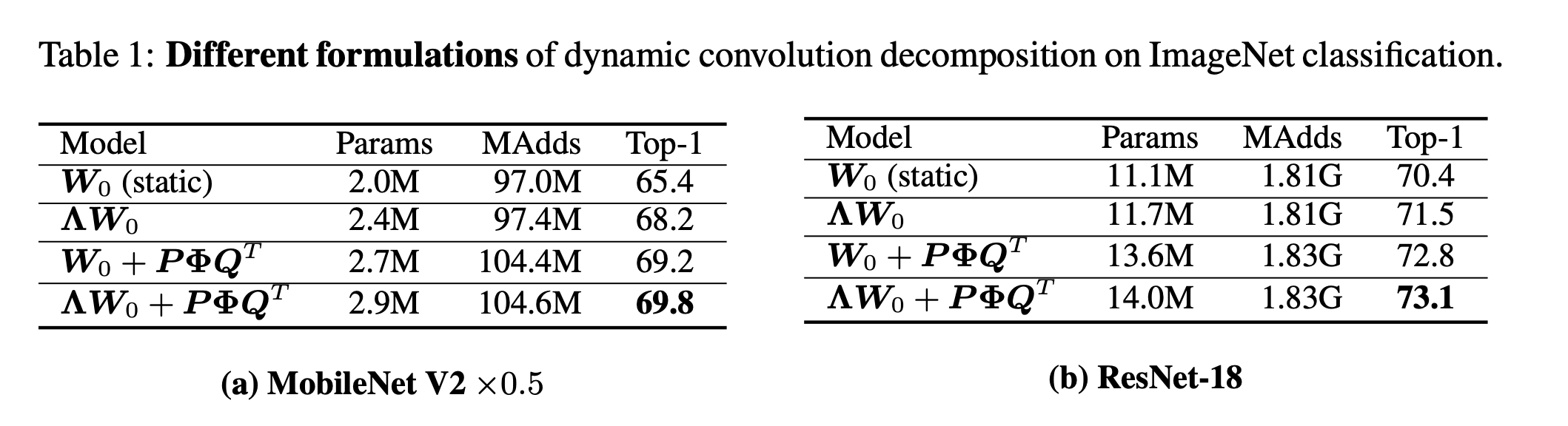
发现\(ΛW_0 + PΦQ^T\)效果最好。
之后作者测试了隐空间维度L的不同取值,结果如下:
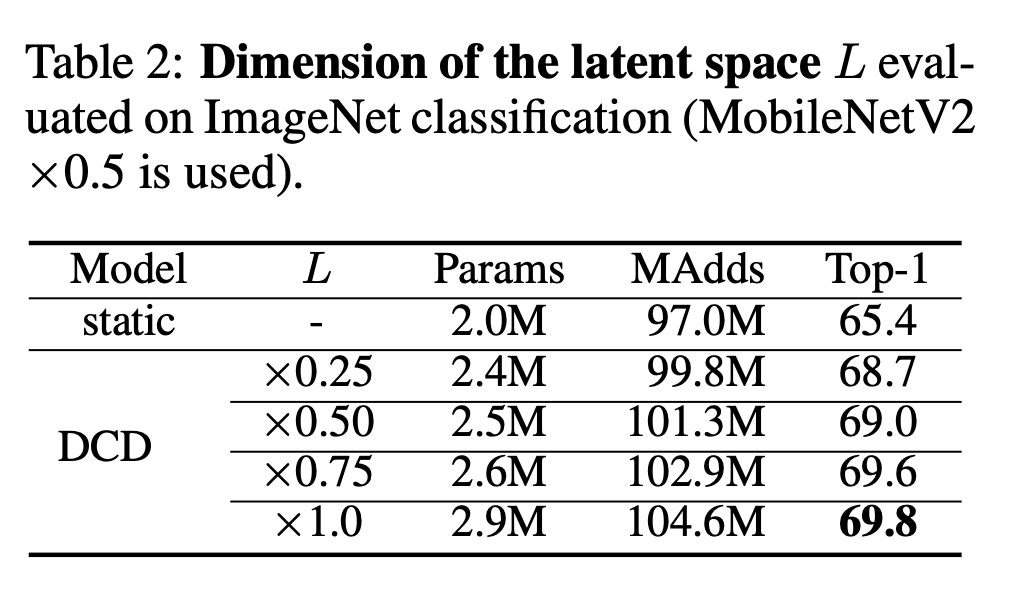
之后还测试了其他超参数的选取,这里不一一列举了。
最后作者对比了其他的动态卷积,结果如下:
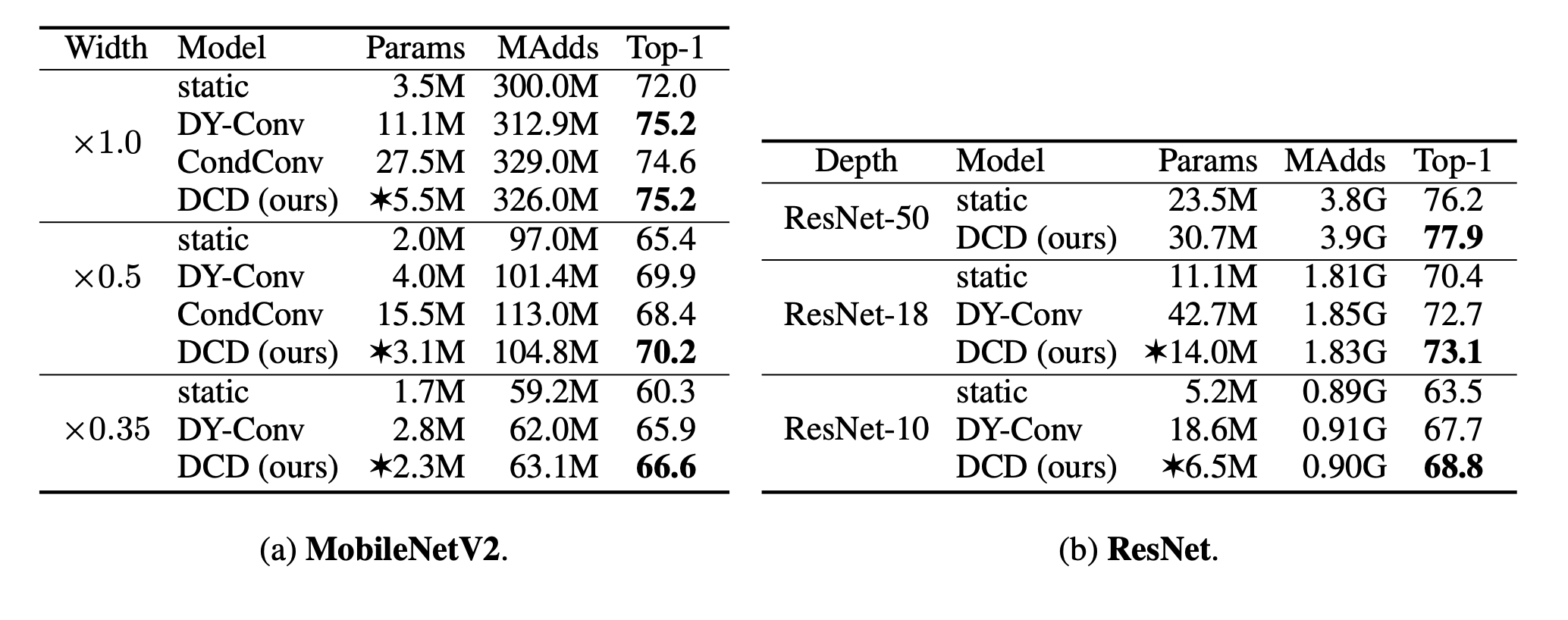
可以看到在大部分情况下DCD可以以较少的参数取得较好的结果。本人在实际测试的时候对比过CondConv和DCD的训练速度,发现DCD的训练时间是CondCOnv的1/3左右,且训练效果好于CondConv。总体来说,该模型更容易学习,精确度也有很大提高,是比较牛逼的~~
最后附上对代码的理解。由于整篇文章比较抽象,代码实现和文章描述的过程不太一样,因此这里参考了一下https://blog.csdn.net/qq_42362891/article/details/119789592这篇博客:
class conv_dy(nn.Module):
def __init__(self, inplanes, planes, kernel_size, stride, padding):
super(conv_dy, self).__init__()
self.conv = nn.Conv2d(inplanes, planes, kernel_size=kernel_size, stride=stride, padding=padding, bias=False)#实现了普通的卷积
self.dim = int(math.sqrt(inplanes))
squeeze = max(inplanes, self.dim ** 2) // 16
self.q = nn.Conv2d(inplanes, self.dim, 1, stride, 0, bias=False)#降维
self.p = nn.Conv2d(self.dim, planes, 1, 1, 0, bias=False)#升维
self.bn1 = nn.BatchNorm2d(self.dim)
self.bn2 = nn.BatchNorm1d(self.dim)
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.fc = nn.Sequential(
nn.Linear(inplanes, squeeze, bias=False),
SEModule_small(squeeze),#这里加了一个小的注意力模块
)
self.fc_phi = nn.Linear(squeeze, self.dim ** 2, bias=False)#论文中的phi矩阵
self.fc_scale = nn.Linear(squeeze, planes, bias=False)
self.hs = Hsigmoid()
def forward(self, x):
r = self.conv(x)#先进行卷积,后对卷积结果加权
b, c, _, _ = x.size()
y = self.avg_pool(x).view(b, c)#平均池化,self.avg_pool(x)尺寸为[b,c,1,1],故加view
y = self.fc(y)#fc层
phi = self.fc_phi(y).view(b, self.dim, self.dim)#phi 即φ,这一步即为φ(x)
scale = self.hs(self.fc_scale(y)).view(b, -1, 1, 1)#hs 即Hsigmoid()激活函数
r = scale.expand_as(r) * r#这里就是加权操作,从公式来看这里应该是A*W0
#实际上这里是 A*W0*x,即把参数的获取和参数计算融合到一块
#fc_scale实现了A*W0
out = self.bn1(self.q(x))#q的话就是压缩通道数
_, _, h, w = out.size()
#这里操作的顺序和示意图不太一样
out = out.view(b, self.dim, -1)
out = self.bn2(torch.matmul(phi, out)) + out#+out是做类似残差的处理
out = out.view(b, -1, h, w)
out = self.p(out) + r#p是把通道维进行升维
return out
之后有时间还要进行深入的研究~
标签:via,Convolution,卷积,Dynamic,self,矩阵,动态,out,通道 来源: https://www.cnblogs.com/lipoicyclic/p/15857166.html
