首页 > 其他分享> > CF1078E Negative Time Summation 题解

CF1078E Negative Time Summation 题解

2022-01-17 20:31:50 作者：互联网

CF1078E Negative Time Summation 题解

一些说明

如果你是由于没有思路而点进题解，那么建议看完 “题目分析” 后自行思考。
如果你在构造过程遇到了困难而点进题解，那么建议看完 “Tips” 后加以应用。
动图中的所有 . 都代表空格子，蓝色方块表示当前机器人所在位置。

简要题意

在无限大的网格图的 \((0, 0)\) 和 \((0, 1)\) 位置有两个二进制数 \(a, b\)，其余位置为空，你有一个机器人，初始在 \((0, 0)\) 位置，支持以下九种操作：

0 / 1，表示把机器人当前位置填上数字 \(0/1\)。
e，表示把机器人当前位置清空。
s，表示这次操作什么都不做。
l / r / u / d，表示机器人向左 / 右 / 上 / 下移动一格。
t，撤销之前所做的 \(\rm num + 1\) 步操作（不会撤销 “撤销操作”），其中 \(\rm num\) 表示当前位置的数字，特别地，若当前位置为空，则什么都不做。

你要构造出一个操作序列，计算出 \(a + b\) 的二进制表示，写在网格图内并让机器人站在答案的最高位，总操作次数不能超过 \(10^5\)。

多测和样例都是假的，题目就是要你构造一个万能的操作序列。

\(1 \le a, b < 2^{30}\)。

题目分析

最好先写一个操作可视化的程序，否则手模起来十分困难。

观察给出的操作，前八种操作都是普普通通的 “顺序结构”，只有第九种操作中出现了类似于 “分支结构” 的功能，考虑以这个操作为突破口进行分析。

根据撤销次数的不同，我们很自然的想到用移动 + 撤销来分类，即：

l, s, t，此时如果当前位置是 \(0\) 或空白都不动，如果是 \(1\) 则回到右边的位置。
s, l, t，此时如果当前位置是 \(0\) 或 \(1\) 都回到右边的位置，只有空白时不动。
r, l, t，此时如果当前位置是 \(1\) 或空白都不动，如果是 \(0\) 则回到右边的位置。

按照这样的方法，就可以把三类格子区分开了。

但是我们没有判断操作，即使区分开三种格子，依然还要做同一件事，只不过做这件事的位置不同了，所以我们的思路就是：“让没用的格子做无用功”。

请认真理解上面这段话，这段话的核心思想贯穿整道题的解答。

现在再回来拆分一下加法的过程：

由于 \(0\) 和空白格的性质不尽相同，先加上前导零，补满 \(30\) 位。
统计每个数位上 \(1\) 的个数，用一些 \(0\) 或 \(1\) 来表示（以 \(0\) 为例）。
从低位开始，对 \(0\) 的个数计数，并考虑进位和当前位的真实结果。

之后就是对每一步分别构造方案了。

Tips

构造方案前，还有一些小 Tips 可以让你少走弯路：

每步操作结束后，最好把多余的字符删掉，这样就不会造成其他影响了。
由于我们分类之后的位置不同，所以每次操作后要进行归位操作，具体地，可以提前造出一堵墙，每次操作之后可以利用墙来归位。例如：这两个位置都可以通过同一种操作回到同一个位置。

如果你找不到归位的路径，不妨把当前位置四周的情况全部画出来，一般来说总能找到一种方案归位。

构造方案

加前导零

朴素的想法是从高到低考虑每一位，如果当前位置是空格就加上一个 \(0\)。

回顾前面提到的核心思想，我们没有判断操作，所以每个位置都要放一个 \(0\)，但是可以通过位置的变化来让后面的 \(0\) 放在无用的位置上，最后把它删掉即可。

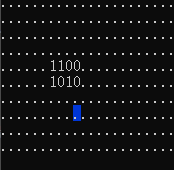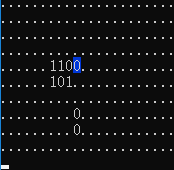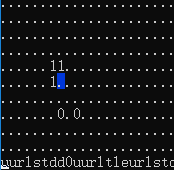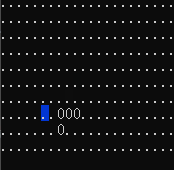
构造方案比较简单，首先在下方两格的位置建一堵墙，之后从下面走上去，通过分类中的第二类操作将空白格和 \(0\) 或 \(1\) 分开，空白格就停下，\(0\) 或 \(1\) 就下来，然后在当前位置放 \(0\)，通过建的墙归位后继续考虑下一位，以 \(1010_2\) 为例：

补完之后把下面两行删掉即可，对于上面的数，翻上去再做一遍即可。

统计个数

依然是核心思想，由于 \(1\) 的个数不确定，所以一定要放两个 \(0\)，那么把 \(0\) 和 \(1\) 分开计数，分别记在左右两列，再把表示 \(0\) 的那一列删掉即可，一些可能的实现细节：

这一列有可能是两个 \(0\) 或两个 \(1\)，需要找到下一行的空位放 \(0\) 来计数。
回退时依然通过原数归位，然后把原数删掉。

我这样做会右偏一格，但无伤大雅，因为我们知道它的相对位置，你也可以相应的添加一些 l 和 r 来使它对齐。

考虑进位，计算结果

现在我们得到了一些 \(0\)，每一列有 \(0/1/2\) 个，且严格按照从上到下给出。

提前建好下面的墙，以及右侧两个边界的 \(0\)，同理，计算完成后删掉即可。

先考虑进位，如果当前位置存在两个 \(0\)，那么一定会进位，直接去左一列找最靠上的空位放 \(0\)，但如果没有，就会在当前列放一个 \(0\)，于是要考虑删掉这个 \(0\)，此时有三种不同情况，对它们分别讨论，利用墙定位和右面已经计算完毕的性质，逐个击破即可，具体实现可以参考动图。

下面考虑计算结果，此时每一位有 \(0\sim 3\) 个 \(0\)，他们的奇偶性就是这一位的答案，依然是核心思想，这里既会出现 \(0\)，也会出现 \(1\)，那么我们必须要 \(01\) 都放，而要让非答案的放在没用的位置上，对这三个位置分类讨论即可，具体实现可以参考动图。

问题到这里也就结束了，不过由于我们补充了 \(30\) 位的前导零，为了更好看，也可以把前导零去掉，方法很容易构造：

最后的方案就是：

<-------------------------- 加前导零 -------------------------->
dd
<---------------- 下面 ---------------->
0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0u
sut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtr
sut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtrsut0dtr
delelelelelelelelelelelelelelelelelelelelelelelelelelelelelele
uerererererererererererererererererererererererererererererere
uuuul
<---------------- 上面 ---------------->
0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0l0d
sdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utr
sdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utrsdt0utr
uelelelelelelelelelelelelelelelelelelelelelelelelelelelelelele
derererererererererererererererererererererererererererererere
ddddl
<-------------------------- 统计个数 -------------------------->
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
uurlstdd0uurltleurlstddddut0uudtuurltledddedeul
<-------------------------- 进位计算 -------------------------->
<---------------- 造墙 ---------------->
rddddll0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0r0uuuur0r0lld
<---------------- 计算 ---------------->
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
lrtudutdut0ddtdtuurtrdutsutluutdlddutueddtdtdtrrruultltlutdtut0u1dddtdtueueuueddl
<---------------- 拆墙 ---------------->
dddlerererererererererererererererererererererererererererererererereuuuurere
<-------------------------- 去前导零 -------------------------->
<---------------- 补零 ---------------->
lllllllllllllllllllllllllllllllll0
<---------------- 去零 ---------------->
ersterstersterstersterstersterstersterst
ersterstersterstersterstersterstersterst
ersterstersterstersterstersterstersterst
<---------------- 归位 ---------------->
r

标签：删掉,uurlstdd0uurltleurlstddddut0uudtuurltledddedeul,题解,位置,当前,操作,Summation,CF1078E
来源： https://www.cnblogs.com/blueqwq/p/15815184.html