【Coel.解题报告】【推柿子的基本思路】[NOI2002] 荒岛野人

题前碎语

还有13天就要期考了，可我还是在机房颓题目。
其实我本来不是很想颓的，可是这道题对于学习扩欧来说很重要，所以还是放进来一下。

题目简介

洛谷传送门

题目描述

克里特岛以野人群居而著称。岛上有排列成环行的 \(m\) 个山洞。这些山洞顺时针编号为 \(1,2,\dots ,m\) 。岛上住着 \(n\) 个野人，一开始依次住在山洞 \(C_1,C_2,\dots ,C_n\)中，以后每年，第 \(i\) 个野人会沿顺时针向前走 \(P_i\) 个洞住下来。

每个野人 \(i\) 有一个寿命值 \(L_i\) ，即生存的年数。

下面四幅图描述了一个有 \(6\) 个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为 \(1,2,3\)；每年要走过的洞穴数依次为 \(3,7,2\)；寿命值依次为 \(4,3,1\)。

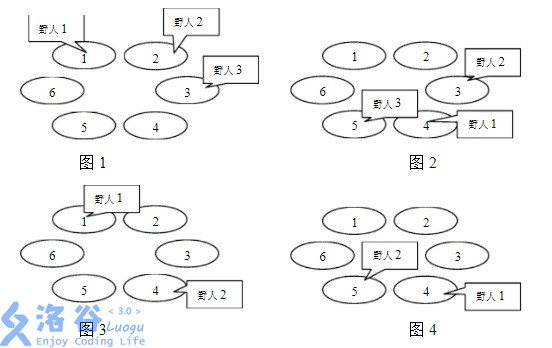
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入格式

第 \(1\) 行为一个整数 \(n(1\leq n\leq 15)\)，即野人的数目。

第 \(2\) 行到第 \(N+1\) 每行为三个整数 \(C_i, P_i, L_i (1\leq C_i,P_i \leq 100, 0\leq L_i\leq 10^6 )\)，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式

仅包含一个数 \(m\)，即最少可能的山洞数。输入数据保证有解，且 \(m\) 不大于\(10^6\)。

---

解题过程

这里描述一下全过程。
假设两个野人\(i,j\)在\(x\)年之后会走到一起，则在\(x\)年后，他们的位置分别是
\((C_i+xP_i) \mod m\)和\((C_j+xP_j) \mod m\)
也就是说，存在一个数\(x \leq (min(L_i,L_j))\)，满足

\[C_i+xP_i \equiv C_j+xP_j \pmod m \]

那么，我们的目标就是找到让这\(n^2\)个同余方程无解的\(m\)取值。
观察到数据范围很小而且\(m\)的范围已知，考虑暴力枚举\(m\)的取值，并用扩欧求解。
代码如下：

#include <cstdio>
#include <cctype>
#include <iostream>
#include <cmath>
using namespace std;

const int maxn = 20;
int n, m, c[maxn], p[maxn], l[maxn];

inline int read() {
	
	int x = 0, f = 1;
	char ch = getchar();
	
	while(!isdigit(ch)) {
		if(ch == '-') f = -1;
		ch = getchar(); 
	}
	
	while(isdigit(ch)) {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	
	return x * f;
}

inline int exgcd(int a, int b, int &x, int &y) {
	
	if(b == 0) {
		
		x = 1, y = 0;
		return a;
	}
	
	int r = exgcd(b, a % b, x, y), tp = x;
	x = y, y = tp - a / b * y;
	
	return r;
}

inline bool solve(int m) {
	
	for(int i = 1; i <= n; i++)
		for(int j = i + 1; j <= n; j++) {
			
			int a = p[i] - p[j], b = m, x, y;
			int gcd = exgcd(a, b, x, y), len = c[j] - c[i];
			
			if(len % gcd != 0) continue;
			a /= gcd, b /= gcd, len /= gcd;
			b = abs(b);
			x = (x * len % b + b) % b;
			if(x <= l[i] && x <= l[j]) return false;//方程有解，说明m不合题意
		}
			
	return true;
}
int main() {
	
	#ifndef ONLINE_JUDGE
	freopen("savage.in", "r", stdin);
	freopen("savage.out", "w", stdout);
	#endif
	
	n = read();
	for(int i = 1; i <= n; i++) {
		c[i] = read(), p[i] = read(), l[i] = read();
		m = max(m, c[i]);//保证m大于等于任意一个c[i]
	}
	
	while(!solve(m)) m++;
	
	printf("%d", m);
	
	return 0;
}

题后闲话

20年的时候这题还是紫题，21年变成蓝题了
虽然这题本来就很水

标签：ch,int,Coel,山洞,leq,野人,NOI2002,基本思路,include
来源： https://www.cnblogs.com/Coel-Flannette/p/15776425.html