发一下这个很经典的图解

---

\[\Huge{常规解法}\]

对于一个矩阵

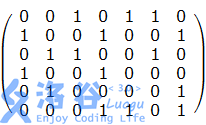
选定它的第一行，将其标为红色，这行的“1”对应的列标为蓝色，蓝色部分的“1”对应的行标为紫色

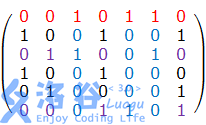
然后删去标了颜色的数字，变成了这样

同理，重复上述操作

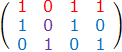
发现得到了一个空矩阵，说明矩阵不合法，回溯，选择第二行

删去有颜色的数字，得到新矩阵

由于剩下的矩阵只有1行，且都是1，选择这一行即可

也就是应该选择原矩阵1中的第1、4、5行

1、从矩阵中选择一行

2、根据定义，标示矩阵中其他行的元素

3、删除相关行和列的元素，得到新矩阵

4、如果新矩阵是空矩阵，并且之前的一行都是1，那么求解结束，跳转到6；新矩阵不是空矩阵，继续求解，跳转到1；新矩阵是空矩阵，之前的一行中有0，跳转到5

5、说明之前的选择有误，回溯到之前的一个矩阵，跳转到1；如果没有矩阵可以回溯，说明该问题无解，跳转到7

6、求解结束，把结果输出

7、求解结束，输出无解消息

---

\[\Huge{DLX算法}\]

Dancing Links的核心是基于双向链的方便操作（移除、恢复加入）

Dancing Links用的数据结构是交叉十字循环双向链

而Dancing Links中的每个元素不仅是横向循环双向链中的一份子，又是纵向循环双向链的一份子。

因为精确覆盖问题的矩阵往往是稀疏矩阵（矩阵中，0的个数多于1），Dancing Links仅仅记录矩阵中值是1的元素

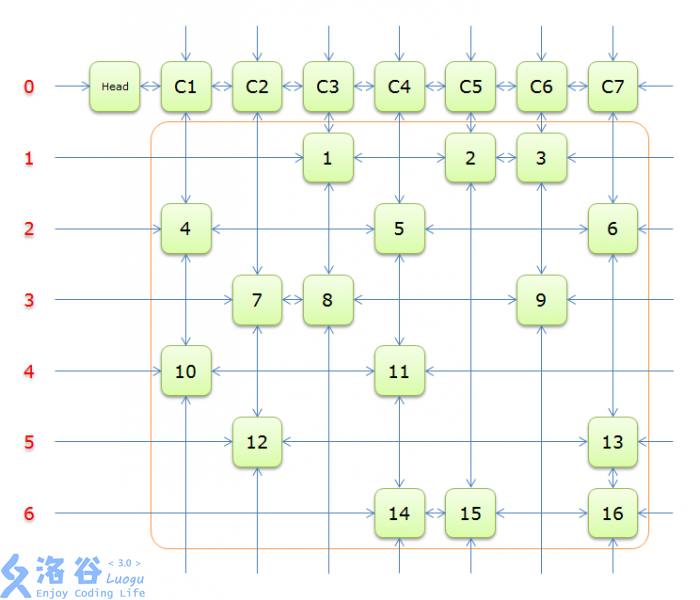
每个绿色方块是一个元素，其中Head和C1、C2、……、C7是辅助元素。橙色框中的元素是原矩阵中1的元素，给他们标上号（从1到16）

左侧的红色，标示的是行号，辅助元素所在的行是0行，其余元素所在的行从1到6

每两个元素之间有一个双向箭头连线，表示双向链中相邻两个元素的关系（水平的是左右关系、垂直的是上下关系）

单向的箭头并不是表示单向关系，而因为是循环双向链，左侧的单向箭头和右侧的单向箭头（上边的和下边的）组成了一个双向箭头，例如元素14左侧的单向箭头和元素16右侧的单项箭头组成一个双向箭头，表示14.Left=16、16.Right=14；同理，元素14下边的单项箭头和元素C4上边的单向箭头组成一个双向箭头，表示14.Down=C4、C4.Up=14

接下来，利用图来解释Dancing Links是如何求解精确覆盖问题

1、首先判断Head.Right=Head？若是，求解结束，输出解；若不是，求解还没结束，到步骤2（也可以判断Head.Left=Head？）

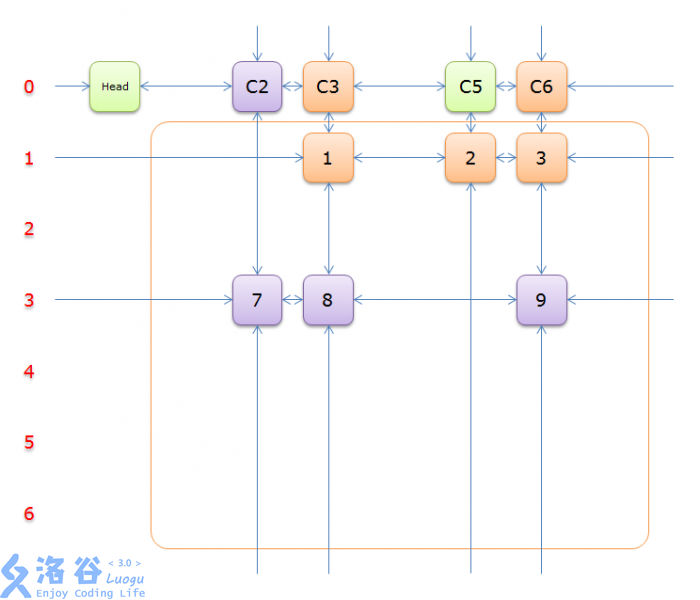
2、获取Head.Right元素，即元素C1，并标示元素C1（标示元素C1，指的是标示C1、和C1所在列的所有元素、以及该元素所在行的元素，并从双向链中移除这些元素）。如下图中的紫色部分。

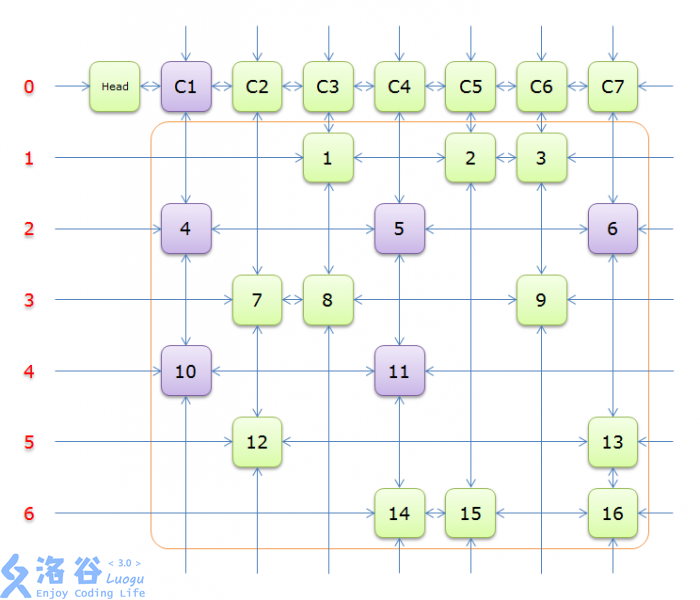
如上图可知，行2和行4中的一个必是答案的一部分（其他行中没有元素能覆盖列C1），先假设选择的是行2

3、选择行2（在答案栈中压入2），标示该行中的其他元素（元素5和元素6）所在的列首元素，即标示元素C4和标示元素C7，下图中的橙色部分。

注意的是，即使元素5在步骤2中就从双向链中移除，但是元素5的Col分量还是指向元素C4的，这里体现了双向链的强大作用。

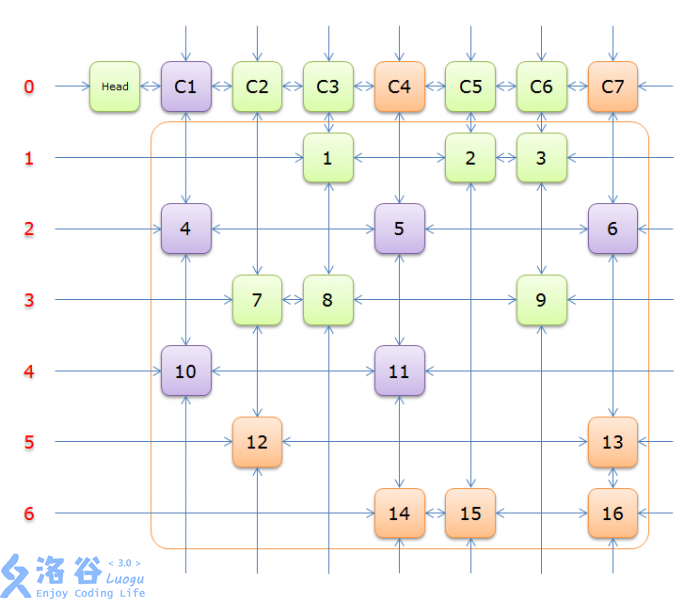
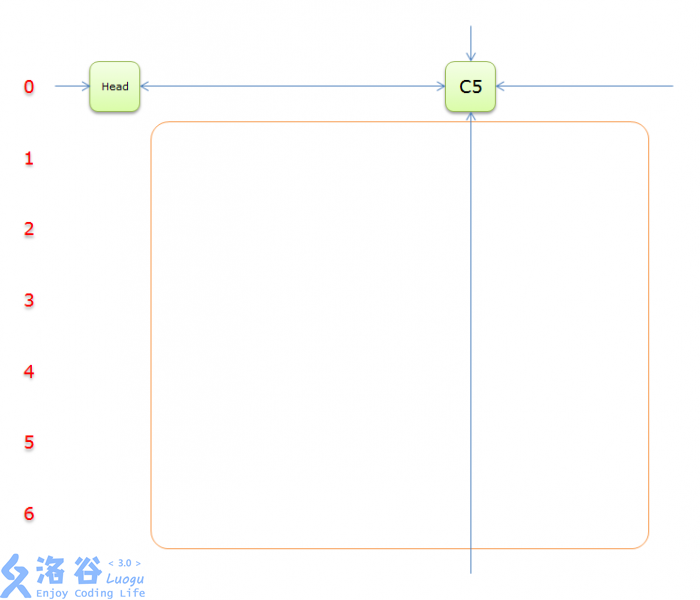
把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

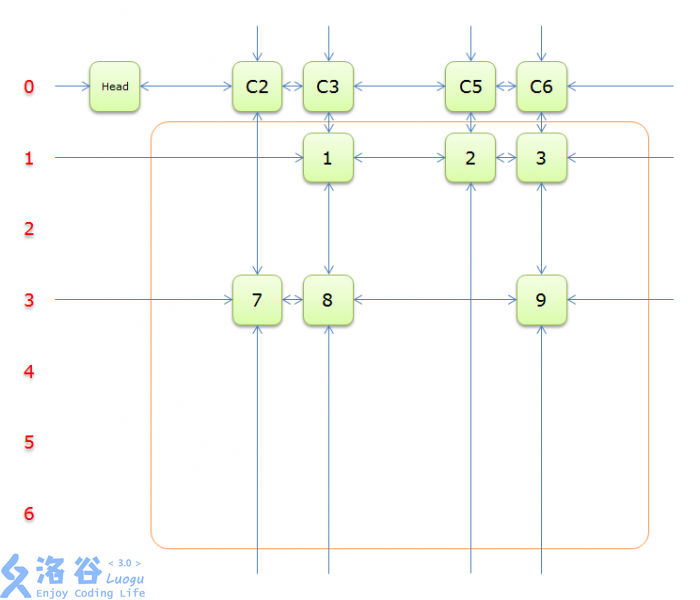
一下排除了很多元素，这样就转换为一个少了很多元素的精确覆盖问题，利用递归，很快就能写出求解的过程

DLX的流程：

1、Dancing函数的入口

2、判断Head.Right=Head？，若是，输出答案，返回True，退出函数。

3、获得Head.Right的元素C

4、标示元素C

5、获得元素C所在列的一个元素

6、标示该元素同行的其余元素所在的列首元素

7、获得一个简化的问题，递归调用Daning函数，若返回的True，则返回True，退出函数。

8、若返回的是False，则回标该元素同行的其余元素所在的列首元素，回标的顺序和之前标示的顺序相反

9、获得元素C所在列的下一个元素，若有，跳转到步骤6

10、若没有，回标元素C，返回False，退出函数。

代码实现：（DLX代码模板）

struct DLX
{
    int n,sz;
    int s[maxn];
    int row[maxnode],col[maxnode];
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];
    int ansd,ans[maxnode];
    void init(int n)//初始化，0为超级节点，1~n为每列的虚拟节点
    {
        this->n=n;
        sz=n+1;
        memset(s,0,sizeof(s));
        for(int i=0;i<=n;i++)
            { U[i]=i; D[i]=i; L[i]=i-1; R[i]=i+1; }
        R[n]=0;L[0]=n;
    }
    void addNodes(int r,const vector<int> &columns)
    {//在第r行（最后一行）添加这些节点
        int first=sz,c_sz=columns.size();
        for(int i=0;i<c_sz;i++)
        {
            int c=columns[i];
            L[sz]=sz-1; R[sz]=sz+1; D[sz]=c; U[sz]=U[c];
            D[U[c]]=sz; U[c]=sz;
            row[sz]=r; col[sz]=c;
            s[c]++;sz++;
        }
        R[sz-1]=first; L[first]=sz-1;
    }
    #define For(i,A,s) for(int i=A[s];i!=s;i=A[i])
    void remove(int c)//覆盖第c个目标
    {
        L[R[c]]=L[c];
        R[L[c]]=R[c];
        For(i,D,c)
            For(j,R,i)//撕开所有相关节点
            { U[D[j]]=U[j]; D[U[j]]=D[j]; --s[col[j]]; }
    }
    void restore(int c)
    {//复原
        For(i,U,c)
            For(j,L,i)
            { ++s[col[j]]; U[D[j]]=j; D[U[j]]=j; }
        L[R[c]]=c;
        R[L[c]]=c;
    }
    bool dfs(int d)
    {
        if(R[0]==0)
        {
            ansd=d;
            return true;
        }
        int c=R[0];
        For(i,R,0) if(s[i]<s[c]) c=i;
        remove(c);
        For(i,D,c)
        {
            ans[d]=row[i];
            For(j,R,i) remove(col[j]);//为了确保只覆盖一次
            if(dfs(d+1)) return true;
            For(j,L,i) restore(col[j]);//回溯
        }
        restore(c);//回溯
        return false;
    }
    bool solve(vector<int> &v)//对外接口
    {
        v.clear();
        if(!dfs(0)) return false;
        for(int i=0;i<ansd;i++) v.push_back(ans[i]);
        return true;
    }
};

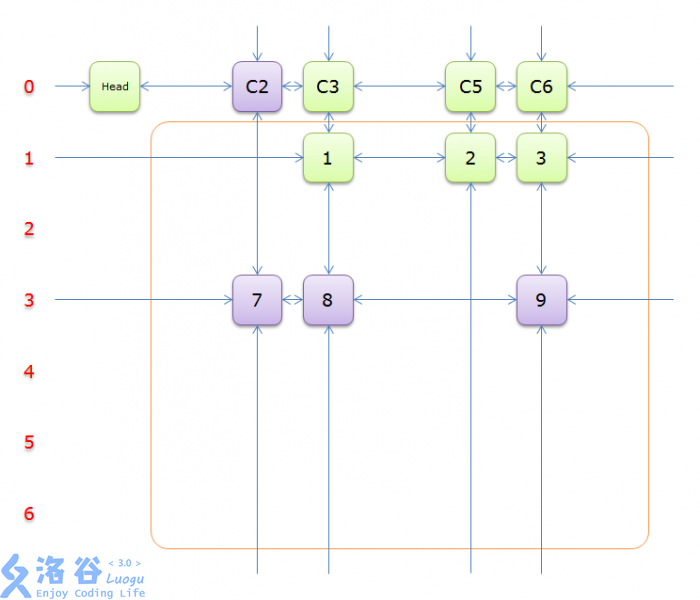
DLX的一次操作如下：（不含回溯）

标签：Head,int,元素,矩阵,标示,舞蹈,双向,DLX,模板
来源： https://www.cnblogs.com/tqr06/p/10458897.html