评测链接

题目大意：

给定一颗有根树，在删去一个点后得到一个森林，而你可以进行一次操作将某个点与其父亲的连边断开并连到另一棵树上，求删去每一个点后操作得到的森林中最大的树最少有多少个点

\(n\leq10^5\)

解题过程：

考虑删去一个点后的森林，操作的点显然要在最大的树中，且连到最小的树上

若有两棵最大的树则答案显然为其大小，不会改变

那么答案即为 \(\max\{MAXsize-size_x,MINsize+size_x,SECsize\}\)，其中 \(MAXsize\) 表示最大的树的大小，\(MINsize\) 表示最小的树的大小，\(SECsize\) 表示次大的树的大小，\(size_x\) 表示操作的点在森林中的子树大小

\(SECsize\) 为固有取值，则我们只需使 \(\max\{MAXsize-size_x,MINsize+size_x\}\) 最小

分类讨论知 \(size_x\) 为所有 \(size\) 中 \(\frac{MAXsize-MINsize}2\) 的前驱或后继时最优

则考虑维护所有 \(size\)

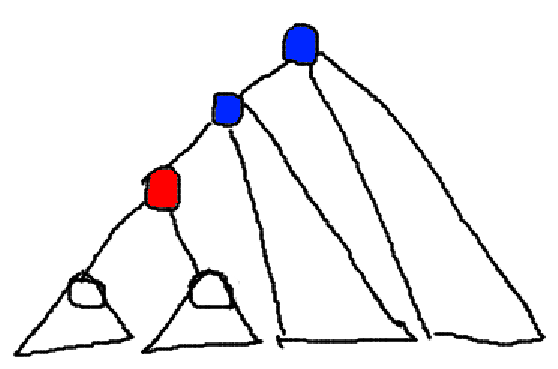
如图，当删去红点时，红点子树的 \(size\) 并不会改变，其祖先的其他子树的 \(size\) 也不会改变，只有其到根的路径上的点也就是蓝点的 \(size\) 减小了

现在考虑维护三个 multiset：\(anc\) 维护到根路径上的点的 \(size\)，\(Q_i\) 维护 \(i\) 号点子树的所有 \(size\)，\(oth\) 维护祖先的其他子树的所有 \(size\)

\(anc\) 最好维护，DFS 时插入，退出时删除，查询 \(i\) 号点的时候带一个 \(\Delta=size_i\) 即可

\(Q_i\) 的维护考虑启发式合并即可

然后是 \(oth\)，由于查询每个点的时候需要保证它的子树的 \(size\) 都不在 \(oth\) 中，所以退出一个子节点后要将它的子树的 \(size\) 再次加入，而因此又要在查询当前点前把这些子树的 \(size\) 再暴力删掉，只有最后一棵 DFS 的子树的 \(size\) 不需要加入和删除，因此考虑重链剖分，暴力加入和删除轻儿子，最后处理重儿子，也就是启发式合并的思路

时间复杂度：\(O(n\log n)\)

上代码：

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<iomanip>
#include<cstring>
#include<algorithm>
#include<ctime>
#include<set>
using namespace std;
inline int read()
{
	int kkk=0,x=1;
	char c=getchar();
	while((c<'0' || c>'9') && c!='-')
		c=getchar();
	if(c=='-')
		c=getchar(),x=-1;
	while(c>='0' && c<='9')
		kkk=(kkk<<3)+(kkk<<1)+(c-'0'),c=getchar();
	return kkk*x;
}
int n,root,head[100001],tot,maxn[100001],sec[100001],minn[100001],size[100001],son[100001],ans[100001],id[100001],cnt,deg[100001];
multiset<int> Q[100001],anc,oth;
struct sb
{
	int to,nextn;
}a[200001];
void ADD(int from,int to)
{
	a[++tot].to=to,a[tot].nextn=head[from];
	head[from]=tot;
}
void format(int u,int fa)
{
	size[u]=1;
	minn[u]=ans[u]=n;
	for(int i=head[u];i!=0;i=a[i].nextn)
	{
		int v=a[i].to;
		if(v==fa)
			continue;
		format(v,u);
		size[u]+=size[v];
		if(size[v]>size[son[u]])
			son[u]=v;
		minn[u]=min(minn[u],size[v]);
		if(size[v]>size[maxn[u]])
			sec[u]=maxn[u],maxn[u]=v;
		else
			if(size[v]>size[sec[u]])
				sec[u]=v;
	}
	if(u!=root)
	{
		minn[u]=min(minn[u],n-size[u]);
		if(n-size[u]>size[maxn[u]])
			sec[u]=maxn[u],maxn[u]=0;
		else
			if(n-size[u]>size[sec[u]])
				sec[u]=0;
	}
	oth.insert(2*size[u]);
}
void check(multiset<int> &T,int maxx,int minx,int &v,int redu)
{
	multiset<int> :: iterator ID=T.lower_bound(maxx-minx+redu);
	if(ID==T.end())
	{
		--ID;
		v=min(v,maxx-((*ID)-redu)/2);
	}
	else
	{
		v=min(v,minx+((*ID)-redu)/2);
		if(ID!=T.begin())
		{
			--ID;
			v=min(v,maxx-((*ID)-redu)/2);
		}
	}
}
void del(multiset<int> &T,int v){T.erase(T.lower_bound(v));}
int calc(int u,int bj){return bj?size[bj]:n-size[u];}
void dsu(int u,int fa)
{
	del(oth,2*size[u]);
	if(u!=root)
		anc.insert(2*size[fa]);
	if(!son[u])
	{
		ans[u]=n-1;
		id[u]=++cnt;
		Q[cnt].insert(2);
		return;
	}
	for(int i=head[u];i!=0;i=a[i].nextn)
	{
		int v=a[i].to;
		if(v==fa || v==son[u])
			continue;
		dsu(v,u);
		for(multiset<int> :: iterator j=Q[id[v]].begin();j!=Q[id[v]].end();++j)
			oth.insert((*j));
	}
	dsu(son[u],u);
	id[u]=id[son[u]];
	for(int i=head[u];i!=0;i=a[i].nextn)
	{
		int v=a[i].to;
		if(v==fa || v==son[u])
			continue;
		for(multiset<int> :: iterator j=Q[id[v]].begin();j!=Q[id[v]].end();++j)
			del(oth,(*j));
	}
	int MAX=calc(u,maxn[u]),SEC=calc(u,sec[u]);
	if(MAX==SEC)
		ans[u]=MAX;
	else
	{
		if(maxn[u])
			check(Q[id[maxn[u]]],MAX,minn[u],ans[u],0);
		else
		{
			check(anc,MAX,minn[u],ans[u],2*size[u]);
			check(oth,MAX,minn[u],ans[u],0);
		}
		ans[u]=max(ans[u],SEC);
	}
	for(int i=head[u];i!=0;i=a[i].nextn)
	{
		int v=a[i].to;
		if(v==fa || v==son[u])
			continue;
		int NOW=id[v];
		if(Q[NOW].size()>Q[id[u]].size())
			swap(id[u],NOW);
		for(multiset<int> :: iterator j=Q[NOW].begin();j!=Q[NOW].end();++j)
			Q[id[u]].insert((*j));
		Q[NOW].clear();
	}
	if(u!=root)
		del(anc,2*size[fa]);
	Q[id[u]].insert(2*size[u]);
}
int main()
{
	n=read();
	for(int i=1;i<=n;++i)
	{
		int u=read(),v=read();
		if(!u || !v)
			root=u+v;
		else
		{
			ADD(u,v);
			ADD(v,u);
            ++deg[u];
            ++deg[v];
		}
	}
	format(root,0);
	dsu(root,0);
    if(deg[root]==1)
        ans[root]=n-1;
	for(int i=1;i<=n;++i)
		printf("%d\n",ans[i]);
	return 0;
}

标签：oth,int,题解,CF768G,maxn,Winds,include,id,size
来源： https://www.cnblogs.com/zhy12138/p/15690816.html