机器学习-一元线性回归与多元线性回归
作者:互联网
目录
前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文主要记录了有关机器学习问题线性模型中的一元线性回归和多元线性回归问题,思路均来源于周志华老师《机器学习》第三章中一元线性回归以及多元线性回归部分的内容。
一、机器学习的三要素
1.模型:根据具体问题,确定假设空间——此篇介绍为线性模型;
2.策略:根据评价标准,确定选取最优模型的策略(通常会产生一个“损失函数”)——此篇以“均方误差”为标准,根据最小二乘法、最大似然估计法来确定损失函数最小的等价条件;
3.算法:求解损失函数,确定最优模型——此篇中计算等价条件中未知数与
的取值。
二、线性模型的基本形式
对于给定的d个属性描述的示例,其中
为
在第
个属性上的取值。
线性模型:学得一个通过属性的线性组合来进行预测的函数形式为:,转化为向量形式为:
。
,将
与
学得之后,模型即可确定。
此种方法的优点在于形式简单,易于建模,可解释性强,其中直观的表达了各个属性在预测中的重要性,即为对标记结果的决定性程度。
以下从回归任务开始,继而讨论二分类和多分类任务。
三、线性回归
对于给定数据集,其中
,
。“线性回归” 意在学得一个线性模型尽可能准确的预测实值输出标记。
3.1一元线性回归
若输入属性的数目仅为一个,则可省略属性的下标,转化为,其中
;
对于离散的属性,若属性之间存在“序”的关系,则可对其进行连续化,以下示例:

一元线性回归目的:学得,使得
,重点即为确定
与
。
根本思路为:以均方误差作为性能量度,即目标为:试图将均方误差最小化。
以下先以“发际线高度”和“计算机水平”的关系一例来讲解两种计算方法,这两种方法殊途同归:
3.1.1最小二乘法
我们假设采集到的样本数据如下图分布:

可以看出样本点偏向于服从线性分布,构造出模型。(图中黑色直线)
要使均方误差最小,即满足:
,其中
与
表示
与
的解;
表示使目标函数f(x)取最小值时的变量值。
对应的几何意义为“欧氏距离”,(对应图中蓝色线段长度),对应损失函数。
这种基于均方误差最小化,利用所有样本到直线上的欧式距离最短来进行模型求解的方法为“最小二乘法”。
3.1.2极大似然估计
对于离散型(或连续性)随机变量,假设其概率质量函数为
,即概率密度为
,其中
为已知样本,例如有
为来自
的n个独立同分布的样本,则
为待估计的参数值(可能为多个)。
其联合概率,即为“多元的概率分布中多个随机变量分别满足各自条件的概率”,用公式表示为:。此为关于
的函数,称为样本的似然函数。
根本想法:使得观测样本出现概率最大的分布即为代求分布,即意向求得使得
取得最大值,即为
的估计值。
具体计算方法参考下例:

另外,我们可以通过对数函数来简化似连乘项,转化为含连加项的对数似然函数:
可大大减少计算量。
下面我们进入比较神奇的一步:
假设线性回归为以下模型:,其中
为不受控制的随机误差,可以假设其服从均值为0的正态分布
,(中心极限定理:在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布),则对应
的概率密度函数为:
,将
用
等价代替可得到下式:
。
可以发现转化为了关于的函数,即为
服从均值为
的正态分布,即
,则可使用极大似然估计的方法来估计
和
的值:

即可转化为:求使得取最大值的情况。
其中m与为常数,则对似然函数的最大化等价于最小化
。
惊讶的发现此等价条件与最小二乘法下得到的公式一样!
下面我们结合这个条件开始求解和
的值:
3.1.3求解  和
和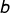
求解思路为:证明为关于
和
的凸函数
利用凸函数求最值的方法来求解出
和
。
①数学分析中对于凸函数的定义与高数中相反:

②多元函数导数的定义:
即为:将函数关于每一个变量的偏导数排列成列向量,以下列出多元函数的一阶导数、二阶导数的表达方式:


③综合以上两类定义,存在以下定理:
类比一元函数判断凹凸性,对于∈
是非空开凸集,
,且
在
上二阶连续可微,则若
的Hessian矩阵在
上是半正定的,则
是
上的凸函数。
则存在转化条件:证明为凸函数
证明海塞矩阵半正定性。

④开始证明矩阵的正定性:
先对各个二阶偏导项进行化简:
=
=
=
=
;
=
=
=
=
;
=
=
=
。
=
=
=
=
;
=
;
=
。
将以上计算结果表达式带入到海塞矩阵中,并通过半正定矩阵的判断定理——顺序主子式非负,整得此矩阵半正定,继而得出为关于
和
的凸函数:

以下只需证明:即可。
证:=
=
=
; 由于
=
成立,
原式转化为: =
=
=
,得证。
⑤根据凸函数求最值的方法求解出 和
:

令两偏导数为0:
=
=0 (i)
(ii)

3.1.4算法处理前的向量化
对于这种连加项,若想要用Python来实现,只能通过用循环,但如果可以对此式进行向量化,则可以转化为矩阵运算,再利用NumPy类库,可大大增加计算效率。
向量化:代入 =
, 转化为:
令,
为去除其均值后的
;
,
为去除其均值后的
。
则 。
3.2多元线性回归
对于给定数据集,更多的情形是样本由
个属性来描述,此时试图学得
,使得
,即为“多元线性回归”。
与一元线性回归的研究方式相似,首先由最小二乘法导出损失函数,再求解其中的参数,将两个参数吸收入向量·形式:
=
。
3.2.1最小二乘法导出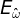
对于,将
也处理成向量乘积的形式,从而简化后续的计算式复杂度,得到与一元回归中类似的形式:

则总体表达式可转化为
;
由最小二乘法可得:即为简化后的损失函数的表达方式。
对损失函数的表达式进行向量化:



3.2.2证明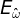 为凸函数
为凸函数
在上述过程中,我们通过对损失函数的向量化,得到它的向量表达式,若想证明其为凸函数,需要通过求取其标量对向量的偏导数,求取其海塞矩阵
,并证明其半正定性(涉及到矩阵分析的内容):


3.2.3求解未知数集合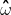
类比一元回归问题,利用凸函数的性质,求取的值:

总结
以上思路来源于《机器学习》这本书第三章的内容,一元线性回归和多元线性回归为本书中的重点内容,公式推导过程复杂但不难理解,条理清晰,需要耐心。内容仅代表个人的思路和理解,如有错误欢迎指正!
标签:一元,函数,回归,凸函数,3.2,3.1,线性 来源: https://blog.csdn.net/qq_46250749/article/details/121336488