机器学习 | 分类性能度量指标 : ROC曲线、AUC值、正确率、召回率
作者:互联网
本篇博客的图源来自 zhwhong,转载仅作学习使用!
在分类任务中,人们总是喜欢基于错误率来衡量分类器任务的成功程度。错误率指的是在所有测试样例中错分的样例比例。实际上,这样的度量错误掩盖了样例如何被分错的事实。在机器学习中,有一个普遍适用的称为混淆矩阵(confusion matrix)的工具,它可以帮助人们更好地了解分类中的错误。
比如有这样一个在房子周围可能发现的动物类型的预测,这个预测的三类问题的混淆矩阵如下表所示:
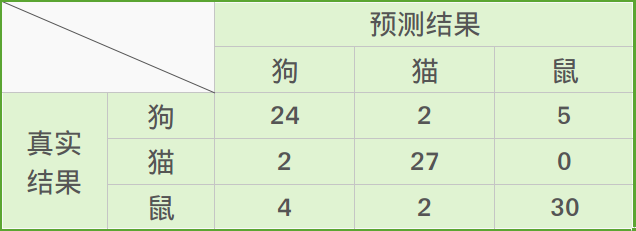
利用混淆矩阵可以充分理解分类中的错误了。如果混淆矩阵中的非对角线元素均为0,就会得到一个近乎完美的分类器。
在接下来的讨论中,将以经典的二分类问题为例,对于多分类类比推断。
二分类问题在机器学习中是一个很常见的问题,经常会用到。ROC (Receiver Operating Characteristic) 曲线和 AUC (Area Under the Curve) 值常被用来评价一个二值分类器 (binary classifier) 的优劣。之前做医学图像计算机辅助肺结节检测时,在评定模型预测结果时,就用到了ROC和AUC,这里简单介绍一下它们的特点,以及更为深入地,讨论如何作出ROC曲线图和计算AUC值。
一、医学图像识别二分类问题
针对一个二分类问题,我们将实例分成正类(positive)和负类(negative)两种。
例如:在肺结节计算机辅助识别这一问题上,一幅肺部CT图像中有肺结节被认为是阳性(positive),没有肺结节被认为是阴性(negative)。对于部分有肺结节的示意图如下:
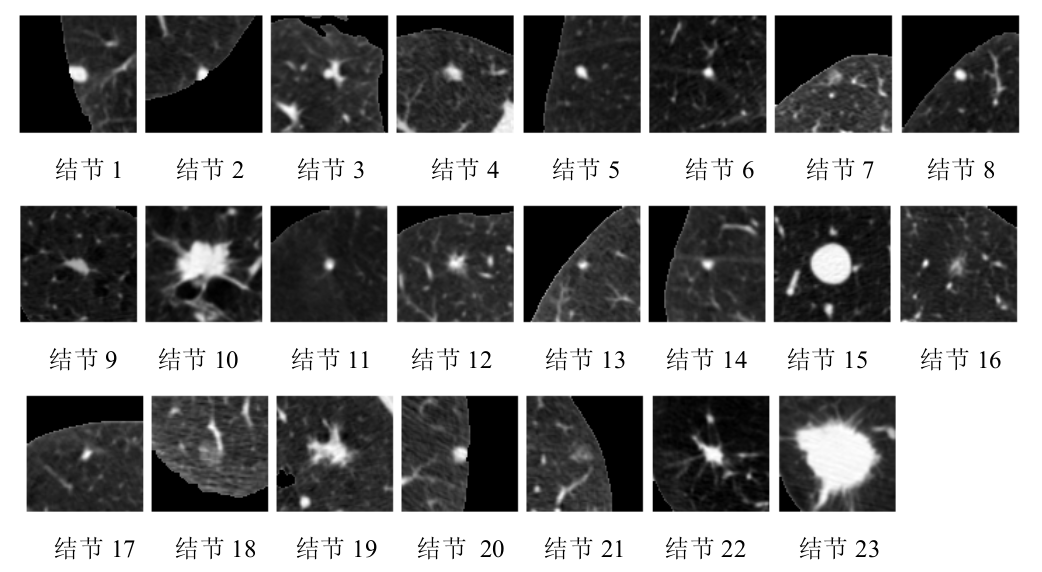
所以在实际检测时,就会有如下四种情况:
(1) 真阳性(True Positive,TP):检测有结节,且实际有结节;正确肯定的匹配数目;
(2) 假阳性(False Positive,FP):检测有结节,但实际无结节;误报,给出的匹配是不正确的;
(3) 真阴性(True Negative,TN):检测无结节,且实际无结节;正确拒绝的非匹配数目;
(4) 假阴性(False Negative,FN):检测无结节,但实际有结节;漏报,没有正确找到的匹配的数目。
详细图解如下:

上图中涉及到很多相关概念及参数,详细请见Wiki上的定义及其混淆矩阵。
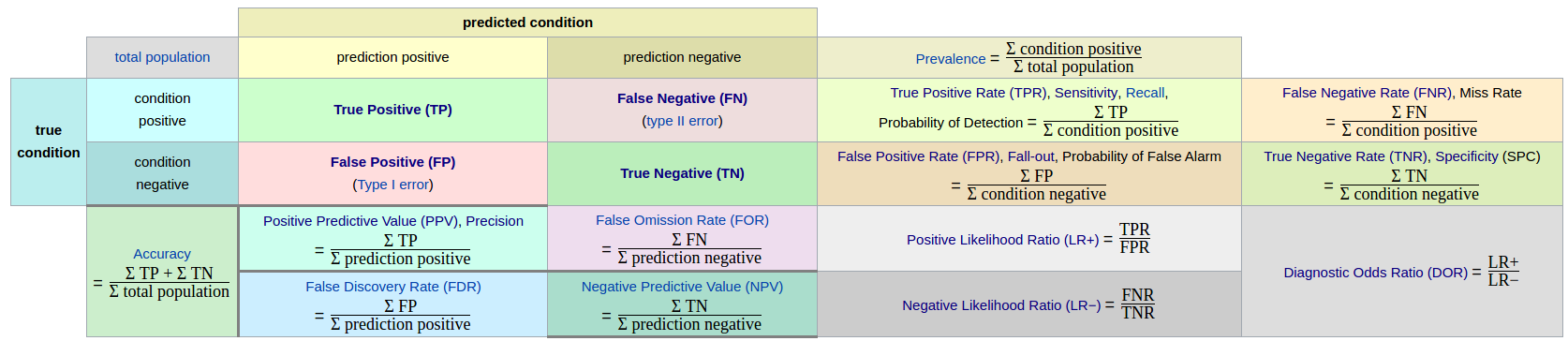
这里整理肺结节识别中的几个主要参数指标如下:
- 正确率(Precision):
- 真阳性率(True Positive Rate,TPR),灵敏度(Sensitivity),召回率(Recall):
- 真阴性率(True Negative Rate,TNR),特异度(Specificity):
- 假阴性率(False Negatice Rate,FNR),漏诊率( = 1 - 灵敏度):
- 假阳性率(False Positice Rate,FPR),误诊率( = 1 - 特异度):
- 阳性似然比(Positive Likelihood Ratio (LR+)):
- 阴性似然比(Negative Likelihood Ratio (LR−) ):
- Youden指数(Youden index):
二、ROC曲线
ROC曲线:接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,roc曲线上每个点反映着对同一信号刺激的感受性。
对于分类器或者说分类算法,评价指标主要有precision,recall,F1 score等,以及这里要讨论的ROC和AUC。下图是一个ROC曲线的示例:
- 横坐标:1-Specificity,伪正类率(False positive rate, FPR),预测为正但实际为负的样本占所有负例样本 的比例;
- 纵坐标:Sensitivity,真正类率(True positive rate, TPR),预测为正且实际为正的样本占所有正例样本 的比例。
在一个二分类模型中,假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
如下面这幅图,(a)图中实线为ROC曲线,线上每个点对应一个阈值。
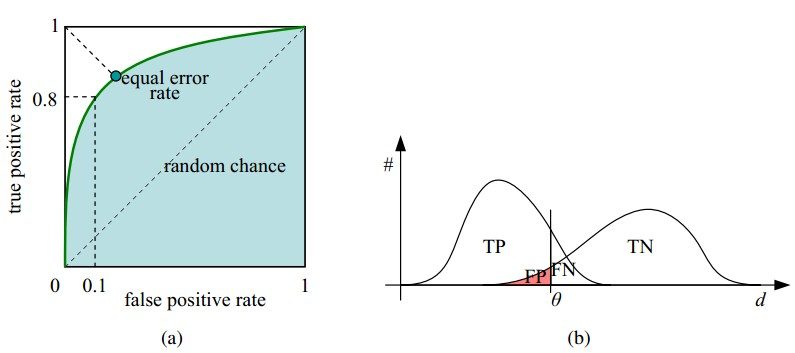
(a) 理想情况下,TPR应该接近1,FPR应该接近0。ROC曲线上的每一个点对应于一个threshold,对于一个分类器,每个threshold下会有一个TPR和FPR。比如Threshold最大时,TP=FP=0,对应于原点;Threshold最小时,TN=FN=0,对应于右上角的点(1,1)。
(b) P和N得分不作为特征间距离d的一个函数,随着阈值theta增加,TP和FP都增加。
- 横轴FPR:1-TNR,1-Specificity,FPR越大,预测正类中实际负类越多。
- 纵轴TPR:Sensitivity(正类覆盖率),TPR越大,预测正类中实际正类越多。
- 理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好,Sensitivity、Specificity越大效果越好。
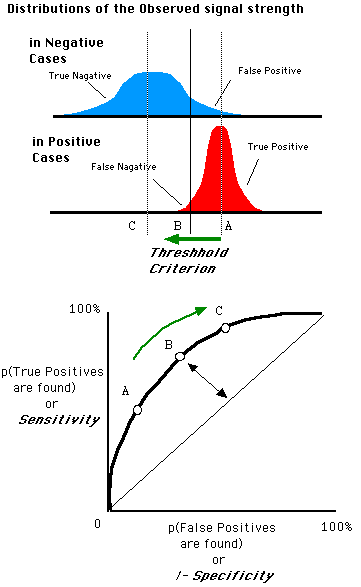
随着阈值threshold调整,ROC坐标系里的点如何移动可以参考:
三、如何画ROC曲线
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值,这又是如何得到的呢?我们先来看一下Wikipedia上对ROC曲线的定义:
In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.
问题在于“as its discrimination threashold is varied”。如何理解这里的“discrimination threashold”呢?我们忽略了分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。通过更深入地了解各个分类器的内部机理,我们总能想办法得到一种概率输出。通常来说,是将一个实数范围通过某个变换映射到(0,1)区间。
假如我们已经得到了所有样本的概率输出(属于正样本的概率),现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。

接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
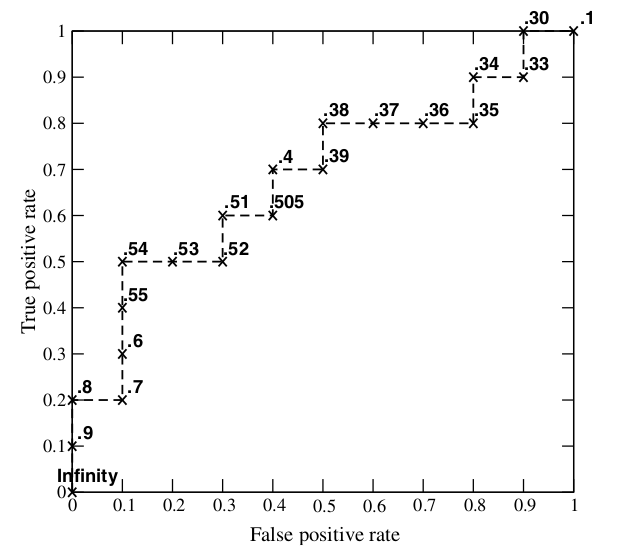
当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
其实,我们并不一定要得到每个测试样本是正样本的概率值,只要得到这个分类器对该测试样本的“评分值”即可(评分值并不一定在(0,1)区间)。评分越高,表示分类器越肯定地认为这个测试样本是正样本,而且同时使用各个评分值作为threshold。我认为将评分值转化为概率更易于理解一些。
四、AUC
AUC值的计算
AUC (Area Under Curve) 被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
AUC的计算有两种方式,梯形法和ROC AUCH法,都是以逼近法求近似值,具体见wikipedia。
AUC意味着什么
那么AUC值的含义是什么呢?根据(Fawcett, 2006),AUC的值的含义是:
The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
这句话有些绕,我尝试解释一下:首先AUC值是一个概率值,当你随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然,AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
三种AUC值示例:
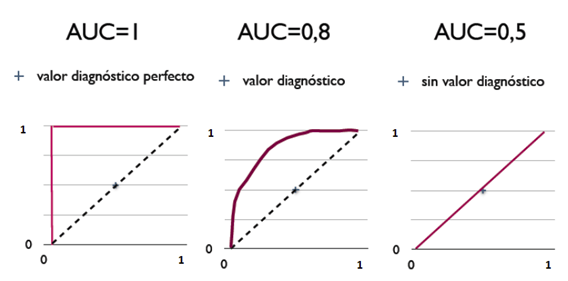
简单说:AUC值越大的分类器,正确率越高。
为什么使用ROC曲线
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比:
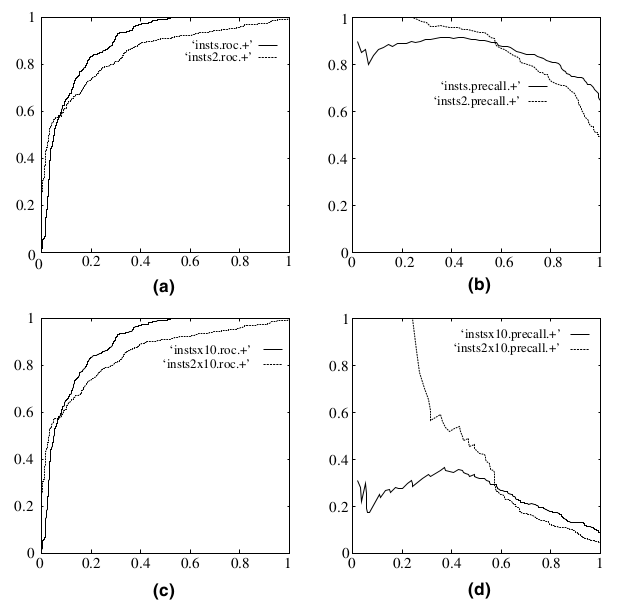
在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
Reference
本文学习自 zhwhong,内容仅供学习使用!
标签:AUC,样本,ROC,分类器,正确率,TPR,曲线 来源: https://www.cnblogs.com/RioTian/p/15463597.html